基于SimHydraulic的加注系统建模与故障仿真

高 欢，张 骏，窦冰冰，智永锋

（西北工业大学 自动化学院，陕西 西安 710129）

航天器在轨加注始于20世纪60年代，指通过航天飞机、飞船等服务航天器对在轨运行航天器的推进剂等耗费品进行在轨补给。目标航天器通过被加注可提高轨道机动能力，增强执行任务的灵活性，延长在轨寿命，该技术成为了航天大国相继进行研究的对象。在我国，目前在轨加注还未进入实际应用阶段，为了确保加注系统的安全性，特别是对于加注过程中的未能预料的偶发性故障，需要在地面进行故障模拟、分析，以设计在轨加注故障诊断系统，确定合理可行的维修方案，甚至需要针对具体故障维修任务开发相应的软、硬件设备。为此进行系统建模与故障仿真具有重大意义[1]。对复杂系统的故障诊断科采用专家系统实现，文献[2]实现了预警专家系统在航天器规避过程中的应用。同时在专家系统中规则匹配可通过模糊Petri网实现[3]。目前，针对于在轨加注故障仿真的研究相对较少，且只针对某一器件，为在轨加注系统建模与故障仿真提供了研究空间与价值。文章通过对模拟加注系统的建模，对系统中各传感器参数的提取，对不同故障征兆的参数信息进行分析，得到系统的故障的不同征兆以实现故障诊断。

1 在轨加注系统模型

在轨加注作为在轨服务的任务之一已具有50多年的历史，是实现航天器气、液等耗费品在轨补给的关键技术。由于空间环境的特殊性，提升了在轨加注系统的难度。美苏等航天大国这一技术已日趋成熟，我国在轨加注研究还处于起步阶段，主要采用的方式为燃料直接传输加注式[4]。

本文采用魏延明等提出的一种基于表面张力贮箱的双组元推进系统在轨加注方案，该方案属于双组元统一推进排气式补给方案中的一种，适合大多数航天器的在轨加注，该方案具有如下优点：与现有卫星推进系统相匹配，改动量最少；没有使用任何活动部件，提高了系统的可靠性；产生的热量比倍压式要少，便于缩短加注时间，提高加注的可靠性和安全性。依据这一方案对空间机动平台在轨补给系统进行了详细设计[5]。通过仿真得到各参考点传感器参数变化，进而确定各故障征兆的故障概率，为模糊Petri网专家系统故障诊断系统搭建提供数据来源[6]。加注模型原理图如下：

图1 加注系统原理图Fig.1 System principle diagram of the filling system

其加注系统分为NTO子系统和N2H4子系统，包括管路以及多个阀门、传感器以及过滤装置。直接传输加注方式的难点在于对贮箱设计、加注密封系统设计的要求很高，且需要较高的可靠性设计。该加注方式的主要原理为：

1）气体补给

提供推进剂加注所需压力，主要通过增压气瓶提供增压气体，关闭目标航天器侧的减压模块，打开手动截止阀3，进行恒压源的高压气体补给。补给完毕后，待目标贮箱压强达到要求时，关闭截止阀，完成气体补给。

2）推进剂补给

在完成航天器对接后，目标航天器贮箱排气，利用目标航天器与补给航天器之间的压差，打开补给侧的加注管路手动截止阀5，将补给航天器贮箱中的推进剂通过管路对目标航天器实行加注任务。由于补给侧需要恒压，因此对其进行增压进行燃料补给。

2 故障仿真原理

在加注系统中，易产生的故障为堵塞和泄漏故障。堵塞故障以管道为主，泄漏可通过加载同一类型的液压缸进行仿真。

1）管道模型

管道总阻力损失为：

Pf为管段沿程阻力损失，Pj为各处局部压力损失。

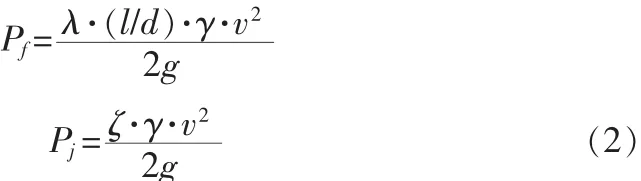
管道液体燃料流速与管道参数间关系如下：

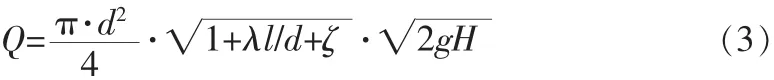
其中l、d分别表示管道长度与管径，λ表示沿程阻力因素，γ表示燃料介质重度，v表示管道截面流速。该模型可用来模拟管道堵塞，即减小管道流体通过面积。

堵塞时，由公式（4）得d减小使得管道沿程压降增大，稳定时间增大。同时由流速公式（5）知管道出口流速低于入口流速。进而引起局部压力损失，因此堵塞状态下加注系统参考点达到稳定状态的时间很长。

2）液压缸模型

其中Vf、Vc分别表示燃料室中流体体积以及几何体积，E为液体燃料体积模量，El代表纯液体燃料体积弹性模量，pa为气压值，VG、VL分别代表参考气压下的气体及液体体积。

在发生泄漏故障时，流体通道增加，同时由于恒流源单位时间流速恒定，因此泄漏管道处液体燃料流速降低。

3 加注系统建模

本文采用Matlab在2007年开发的SimHydraulic模型库进行Simulink仿真，前人利用SimHydraulic对机构液压仿真、流体管网以及给排水进行仿真，并取得很多成果。文章针对加注系统结构性质，分为气体补给与推进剂补给。分别对气路和液路系统进行建模并得到在堵塞和泄漏情况下的系统参数变化曲线。

3.1 气路系统建模

1）气源模块

在加注开始时，需要对系统进行高压气体补给，因此需要提供恒压气源。选择SimHydraulic模型库中的Hydraulic Pressure Source搭建恒压气源，通过Constant中的数据对恒压气源的大小进行设定。

2）控制模块

气路系统中主要控制模块包括减压器和气动球阀。

当减压器（Pressure Relief Valve）阀门入口处压强小于设定压强时，阀门保持关闭，当达到阀门预设压强值时，阀门控制机构强制偏离产生通道，使得液体从孔径流出，在内部产生压降，达到维持压强在合理工作范围内的目的。主要设定参数有：最大流通面积、阀门设定压强、阀门调整范围以及液体损失率。通过对减压器的标准压强以及压强范围的设定，使得作用在推进剂贮箱内的压强维持恒定。

气动球阀（Ball Valve）的作用是控制加注气路的通断，控制加注进程，流速与孔径开度及球阀压差成比例。过滤器是为了过滤气源中的固体杂质，避免进入推进剂贮箱引起故障，过滤器主要在气路中起到类似液阻的作用，因此用模型库中的Local Resistance进行模拟，该模块还可进行弯管以及配件等的模拟。

3.2 液路系统建模

由于两种液路结构相同，仅对单一NTO液路进行建模分析。

1）液源模块

液源模块采用模型库中的Hydraulic Constant Flow Rate Source进行仿真。该恒流源代表在外界压力变化的前提下，依旧可以提供恒定流速的液体，液体流速可通过模块参数进行设置。

2）控制模块

同液路系统相似，控制模块包括气动球阀，管道以及传感器。在仿真过程中，气动球阀的外接信号设为阶跃信号。管道采用模型库中Hydraulic Pipeline仿真，该模块可仿真圆形或非圆形界面管道，可用来描述管道的摩擦阻力对液体参数的影响。

4 故障仿真

目前我国的有人在轨服务还处于研究阶段，随着载人航天的发展，使得我国的宇航员在轨时间不断延长，为未来在轨服务提供了重大的生命保障技术。由于系统要求高安全性，推进剂的泄漏以及管道的堵塞是最常见以及危险的，一旦发生将会造成巨大的经济以及优秀人才的损失，因此尽可能的还原加注过程，并对其进行常见的故障仿真是十分必要的。结合上文得出的加注系统模型，分别对堵塞和泄漏故障进行仿真。

4.1 堵塞故障仿真

堵塞可通过改变管道的pipe internal diameter（管道内径）参数进行仿真，内径越小，表明堵塞情况愈严重。假设内径参数为b2>b1>b3，b3=0.03 m为正常管道内径，b3=0.02 m为轻微堵塞，b3=0.01 m为严重堵塞。得到Local_B、Local_C两点在堵塞时压强变化相同，具体3种情况下的Local_A、Local_B、Local_C三点的压强、流量变化曲线如下：

图2 堵塞状态下Local_A点压强变化Fig.2 Pressure change of Local_A in the blocked state

图3 堵塞状态下Local_B点压强变化Fig.3 Pressure change of Local_B in the blocked state

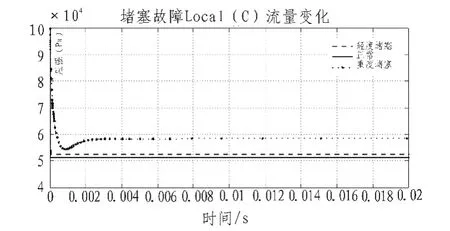
图4 堵塞状态下Local_C点流量变化Fig.4 Flow change of Local_C in the blocked state

由图可知，在轻微堵塞的情况下，Local_A、Local_B点初始压强减小，Local_A点稳定压强变小，Local_B点最终压强与恒压气源压强相等。在严重堵塞的情况下，Local_A、Local_B点压强小与恒压气源压强，且Local_A点压强在严重堵塞状态下呈现凹点。Local_B点在堵塞情况下稳定时间逐渐减小，最终在严重堵塞下为零。在管道堵塞时，位于燃料缸后的管道入口处Local_C点流量会因为堵塞而增加，出口Local_D处则相反。

4.2 泄漏故障仿真

泄漏故障可通过在液路系统中加入一个液压室（Constant Volume Hydraulic Chamber）进行模拟。

1）经过气路仿真得到泄漏情况下系统Local_A、Local_B、Local_C三点处的压强变化如图5~6示。

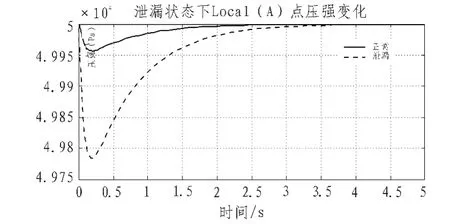
图5 泄漏时Local_A点压强变化Fig.5 Pressure change of Local_A in the leaking state

图6 泄漏时C点压强变化Fig.6 Pressure change of Local_Cin the leaking state

Local_B点压强变化与Local_C点相同。

2）泄漏时液路仿真得到泄漏情况下系统Local_C、Local_D两点处的流量变化如图7~8示。

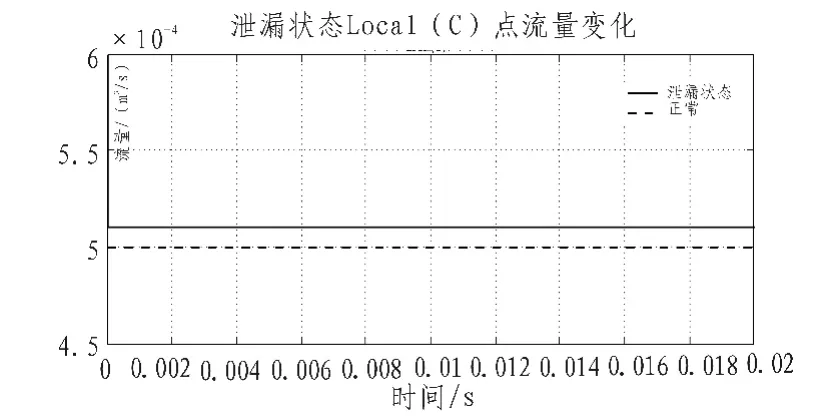
图7 泄漏状态下Local_C流量变化Fig.7 Flow change of Local_Cin the leaking state

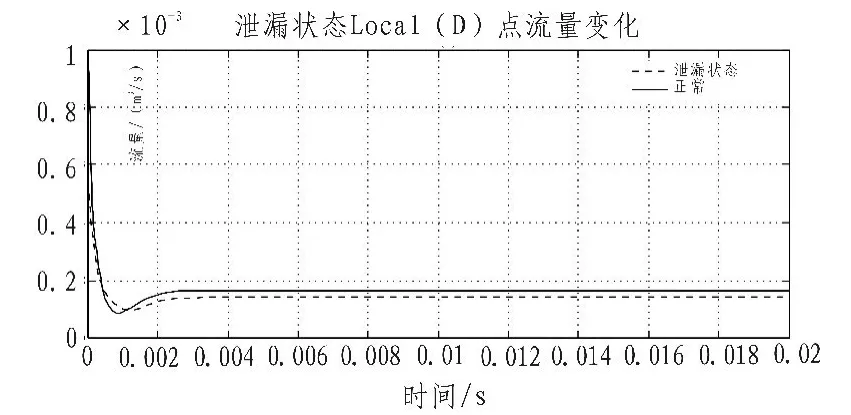
图8 泄漏状态下Local_D点流量变化Fig.8 Flow change of Local_D in the leaking state

经过对模型公式分析可知，正常情况下，Local_B、Local_C点由于过滤器产生的压差，在t=0时刻PB=PC

5 故障分析

经过加注系统建模以及故障模式仿真得到堵塞和泄漏故障征兆集见表1，括号内代表压强以及流量变化，单位分别104Pa为以及10-4m3/s

表1 各故障状态下压强以及流量变化趋势Tab.1 Pressure and flow change of each fault condition

除了稳定状态下下压强以及流量的变化，另一个故障诊断参数为系统参考点到达稳定状态下的时间变化，具体变化趋势如表2所示。

表2 各故障状态下压强以及流量稳定时间变化趋势Tab.2 Pressure and flow stability time of each fault condition

综上所述，在系统轻微堵塞状态下，核心参考点为qC、PA，qC出现增大时，系统为堵塞状态，此时若PA数据下降幅度较小，即为轻度堵塞反之即为重度；在重度堵塞状态下核心参考点为，若Local_B点压强下降且Local_A点压强达到稳定状态的时间明显增大，即为重度堵塞；泄漏状态下以Local_C、Local_D两点流量为核心，均减小即为泄漏状态，并以Local_A、Local_B、Local_C三点稳定状态需要的时间为参考，若该三点压强稳定时间均增大即为泄漏。

6 结 论

文章针对在轨加注采用Matlab中的Simhydraulic模型库对系统进行了建模，并结合模块参数，实现常见故障的仿真，对实际研究具有参考价值。通过仿真可得加注过程中堵塞以及泄漏状态下的核心征兆，并实现常见故障状态下加注系统参数的变化趋势，对深入在轨加注理论研究以及实际试验具有重要的指导意义。同时，通过得到的常见故障状态核心征兆，为基于模糊Petri网模型的故障诊断专家系统的建立提供了推理依据。

[1]陈小前，袁建平，姚雯，等.航天器在轨服务技术[M].北京:中国宇航出版社，2009.

[2]钱宇，徐敏，郭东，等.基于预警专家系统的航天器规避研究[J].计算机仿真，2011（5）:93-96.QIAN Yu，XU Min，GUO Dong，et al.Spacecraft collision avoidance maneuver study based on warning expert system[J].Computer Simulation，2011（5）:93-96.

[3]刘剑刚，高洁，王明哲.模糊Petri网及其在模糊推理中的应用[J].计算机仿真，2004（11）:152-154.LIU Jian-gang，GAO Jie，WANG Ming-zhe.Fuzzy petri net and its Application in uncertain reasoning[J].Computer Simulation，2004（11）:152-154.

[4]高明，胡茑庆，秦国军.面向对象的推进剂加注系统建模与故障仿真[J].机床与液压，2009，37（9）:223-226.GAO Ming，HU Niao-qing，QIN Guo-jun.Object-oriented modeling and fault simulation of propellant filling system[J].Machine Tool&Hydraulics，2009，37（9）:223-226.

[5]魏延明，潘海林.空间机动服务平台在轨补给技术研究[J].空间控制技术与应用，2008，34（2）:18-22.WEI Yan-ming，PAN Hai-lin.Research on on-orbit refueling of maneuverable platform[J].Aerospace Control and Application，2008，34（2）:18-22.

[6]高梅梅，吴智铭.模糊推理Petri网及其在故障诊断中的应用[J].自动化学报，2000，26（5）:677-680.GAO Mei-mei，WU Zhi-ming.Fuzzy reasoning petri net and its application to fault diagnosis[J].Acta Automatica Sinica，2000，26（5）:677-680.