基于改进遗传算法的模拟电路参数自动化设计

李红磊，刘家学

（中国民航大学 航空自动化学院，天津 300300）

模拟电路自动化设计方法和工具缺乏，设计成本高。近二十年学者对模拟电路的自动化设计进行了大量研究，早期的 Koza 等人研究的遗传编程（Genetic Programming， GP）[1]和Lohn等提出的轨迹编码方法[2]都能完成电路的自动进化，但运算量巨大且前期需要大量的编程工作，移植难度较高。文献[3]将理想模型和遗传算法相结合进行运算放大器的设计，简化了运算量，文献[4]提出包含多目标适应度评估的自适应遗传算法，提高了进化的寻优能力，但这些方法着重电路结构的设计。随着模拟电子技术的不断进步，在振荡器、放大器、滤波器等很多应用领域，模拟电路已具有比较成熟的电路结构，如何根据不同的性能要求，快速准确的完成电路参数设计，是设计人员日益关心的问题。

文中用电路性能达标程度的加权和作为适应度评价函数，建立了模拟电路数学评价模型。采用竞争择优交叉算子提高了子代优生率，加快了算法的收敛速度，运用自适应和超突变相结合的改进交叉变异策略，增强了算法局的部搜索能力。针对遗传算法搜索结果与常用元件参数难以匹配的缺点，通过限定可选参数集，将最优染色体基因所代表的元件参数转变成可行参数。

1 模拟电路评价模型的建立

模拟电路的结构复杂多样，难以根据其物理意义建立统一的数学模型，因此提出以电路性能达标程度建模的思想。电路性能的设计要求可以分三类描述，第一类是要求某性能等于指定值，例如振荡电路的中心频率，滤波器的截止频率等；第二、三类是要求某性能大于或小于指定值，例如放大电路的放大倍数，电路的工作电流等。设fi（x）为第i个性能目标的性能方程，fbesti为相应的设计目标值。则性能达标程度函数描述如下

3）第三类设计要求：ui（x

模拟电路的设计一般为多目标设计，根据重要程度为每个目标赋予权值则适应度评价函数可如式（4）表示。

2 遗传算法的改进

2.1 竞争择优交叉算子

常规遗传算法中一对父代染色体只产生一对子代，难以保证子代个体的优良性。模拟自然界生物一对父代产生多个子代，并且子代个体也存在相互竞争的现象，结合两点交叉策略建立不同于常规遗传算法的交叉算子[6－7]。设 xm=（xm1，xm2，…，xmn），xf=（xf1，xf2，…，xfn）为选中的一组父代染色体，通过交叉产生8个子代染色体：

表示 xmk、xfk中较大基因，min（xmk，xfk）（1≤k≤n）表示 xmk、xfk中较小基因。八个子代染色体覆盖了整个父代基因域，从中选出适应度最高的两个作为子代个体，通过竞争提高子代优生率。

2.2 突变策略

模拟电路参数取值区间跨度大，单一的变异尺度难以兼顾各参数的进化需求，应根据每个元件参数取值特点分别确定变异基准尺度，设 x=（x1，x2，…，xk，…，xn）为选中突变染色体，xk为选中变异基因，l∈（0，1）。μk为 xk的变异尺度，应根据元件取值区间和取值特点确定大小，设Lk为xk取值区间长度，α根据情况，一般取0.1～0.2。突变算子可描述如下

2.3 交叉、变异策略

进化前期，为实现种群多样性的目标，需要提高交叉概率。进化后期，为了保护优良个体，通用做法是将优良个体的交叉概率设置很低甚至为零，但这种方法导致了遗传算法可能陷入局部最优解的隐患。染色体突变打破了子代继承父代的基因进化模式，为进化提供了更多的可能性，在变异尺度合适的前提下，突变具有远超交叉的局部搜索能力，因此对高适应度个体采用高突变的进化策略。交叉概率和突变概率如下所示

式中fmax为最大个体适应度，fbest为理想适应度，favg为种群平均适应度，f为要交叉的两个个体中较大的适应度，f′为要变异个体的适应度值，Pc1=0.9，Pc2=0.1，Pm1=0.4，Pm2=0.1，Pm3=1。 对于适应度大于0.99fbest的高适应度个体采用精英保留策略，如果突变后适应度降低，则仍将突变前个体纳入子代，防止高突变对精英个体的破坏[8－9]。

2.4 最优解的可实现处理

设计人员能够选用的元件参数是有限的，而遗传算法求出解是一段连续区间内的随机搜索结果，导致遗传算法求出的元件参数虽然能够满足性能要求，但却难以完成实际应用。因此需要对遗传算法的结果做进一步的处理，用Objecti表示基因xi的可选元件集，Gm（xi）表示处理后的xi，则可实现化处理可描述如下

为减小基因可实现化处理对适应度的影响，先处理取值限制最大的基因，接着以尽量保持适应度不变为目标，重新计算未处理基因的值，再对限制较大基因进行可行化处理，重复上述过程，直到所有基因处理完毕。

3 应用实例

电压控制振荡器（VCO）是一种振荡频率随外加电压变化的振荡器，是现代通信系统电路中的重要单元。VCO核心结构[10]如图1所示，目标性能参数如表1所示。

3.1 建立适应度评价函数

决定振荡频率的元件是 C1、C2、CV、CS、L，因此染色体向量为 x={L，CV，C1，C1，Cs}。 CV是调谐用压控电容，选用变容二极管BB202，它在反向电压0～5 V区间内具有很好的线性度和较大的容值域度6～25 pF。为保证电路具有最好的调频区间，当CV=1/2Cd=15 pF时，振荡频率应恰好等于调频区间的中心频率。VCO的振荡频率性能方程为

图1 克拉普振荡电路原理图Fig.1 Clapp oscillation circuit schematic

表1 压控振荡电路技术参数Tab.1 The parameters of VCO

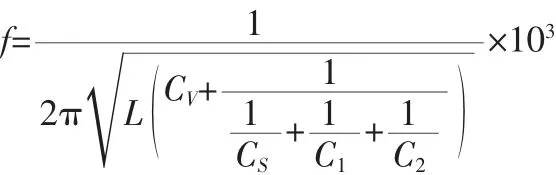
理论调谐下限频率为fmin=fCV=25pF，调谐上限频率为fmax=fCV=6pF，中心频率达标程度函数u1（xi）和调谐范围达标程度函数 u2（xi）可由式（11）～（14）表示，适应度评价函数如式（15）所示。

3.2 确定搜索区间、变异尺度

振荡频率较高时三极管的极间电容也会成为振荡频率的影响因素，因此C1、C2的取值应大于极间电容。Cs与C1、C2构成串联关系，为保证CV的变化能够起到足够的频率调节作用，Cs的取值应小一些，从而削弱C1、C2对振荡频率的影响比重。本文电感用线径0.1mm的漆包线绕制，线圈直径6mm，因为线圈绕制匝数越多，自分布电容越大且自谐振频率越低，所以线圈匝数控制在2至10圈。通过以上分析确定各参数的搜索区间和变异基准尺度如表2所示。

3.3 结果分析

初始种群数量、进化代数设为50。采用VC++作为程序设计平台，算法流程如下：

表2 参数搜索区间Tab.2 The searching space of the parameters

1）随机产生初始种群，由n个实数染色体构成，每个基因代表一种元件参数。

2）计算种群最佳适应度fbest，种群平均适应度favg。

3）轮盘赌选出父代个体，计算交叉概率Pc、遗传概率Pm，交叉变异产生子代种群，并计算种群最佳适应度fbest，种群平均适应度favg。

4）是否达到最大进化代数。若达到停止，若未达到，转到第三步。

5）对最佳适应度进行可实现处理，之后停止。

运行结果如图2所示，由于采用子代竞争择优的交叉策略，改进遗传算法进化初期种群的最佳适应度就有了很大提高，随着进化代数的提高，传统遗传算法进化逐渐停滞，而改进遗传算法的最佳适应度仍在不断提高，证实了改进遗传算法在进化后期具有更强的局部搜索能力。表3为处理前后元件参数对照，可以看出，培养后的参数对设计人员更具实践意义。

图2 改进前后遗传算法最佳适应度曲线Fig.2 The optimal fitness curve of the normal and improvement genetic algorithm

表3 可实现处理前后参数变化Tab.3 The changes of parameters before and after the realizable treatment

利用表3提供参数制作振荡电路，其中电感的制作如表4所示。由于电容容差、BB2O2的特性误差以及电感制作误差等干扰因素的存在，实际电路振荡频率可能偏离115MHz，需手动微调线圈间距进行修正。为解决工作温度变化引起的中心频率的抖动，用锁相环芯片提供变容二极管输入电压。用示波器检测振荡电路中心频率，结果如图3所示。

表4 103nH电感制作Tab.4 The production of 103nH inductance

图3 振荡电路中心频率示波器观测图Fig.3 The oscilloscope graph of oscillating circuit's center frequency

4 结束语

文中结合模拟电路特点，利用性能达标程度建立评价函数。并对遗传算法做了几点改进，采用竞争择优交叉算子提高子代优生率，基于精英保留的高突变策略提高了算法的局部搜索能力。通过可实现处理，完成遗传算法最优解到可行解的转变。仿真结果表明，算法的收敛速度和寻优精度都得到了有效提高。压控振荡电路的设计成功验证了方案的可行性，设计人员可以通过修改适应度函数，将该方案应用于其他模拟电路的设计。但此方案对设计者的知识、经验要求较高，如何将模拟电路设计师的知识融入刚方案，实现电路参数和结构的全自动化设计还有待进一步研究。

[1]Lohn JD，Colombano SP.Acircuit representation technique for automated circuit design[J].IEEE Transactions on Evolutionary Computation，1999，3（3）:205-219.

[2]Koza JR，Bennett FH，Andre D，et al.Automated synthesis of analog electrical circuits by means of genetic programming[J].IEEE Transactions on Evolutionary Computation，1997，1（2）:109-128.

[3]张左钊，宋绍民.基于理想模型和遗传算法的模拟电路自动化设计研究[J].电子技术应用，2008（4）:47-53.ZHANG Zuo-zhao，SONG Shao-min.Research of automated design of analog circuit based on idealized model and genetic algorithm[J].Application of Electronic Technique，2008（4）:47-53.

[4]郑维山，彭艺频，张萌，等.一种新的CMOS模拟单元单路优化设计方法[J].应用科学学报，2006，3（2）:150-153.ZHENG Wei-shan，PENG Yi-pin，ZHANG Meng.Anew design method in CMOS analog cell circuit optimization[J].Journal of Applied Sciences，2006，3（2）:150-153.

[5]梁戈超，何怡刚，朱彦卿.基于模糊神经网络融合遗传算法的模拟电路故障诊断法 [J].电路与系统学报，2004，4（2）:54-57.LIANG Ge-chao，HE Yi-gang，ZHU Yan-qing.Method of analog circuit fault diagnosis based on fuzzy neural network and genetic algorithm[J].Journal of Circuits and Systems，2004，4（2）:54-57.

[6]任子武，伞冶.实数遗传算法的改进及性能研究[J].电子学报，2007，35（2）:269-274.REN Zi-wu，SAN Ye.Improvement of rea-lvalued genetic algorithm and performance study[J].Acta Electronica Sinica，2007，35（2）:269-274.

[7]任子武，伞冶.自适应遗传算法的改进及在系统辨识中应用研究[J].系统仿真学报，2006，18（1）:41-43.REN Zi-wu，SAN Ye.Improved adaptive genetic algorithm and its application research in parameter identification[J].Journal of System Simulation，2006，18（1）:41-43.

[8]Sangameswar Venkatraman，Gary G.Yen.ASimple Elitist Genetic Algorithm for Constrained Optimization [J].Computational Intelligence and Security，2006 International Conference，2006（1）:402-405.

[9]Chu M，Allstot D J.Elitist nondominated sorting genetic algorithm based RF IC optimizer[J].IEEE Transactions on Circuits and Systems I:Regular Papers，2005，52 （3）:535-545.

[10]铃木宪次.高频电路设计与制作[M].北京：科学出版社，2005:84-93.