MasterCAM下刀位置对切削路径的影响

江苏省徐州市中等专业学校 蔡佩璋

MasterCAM软件在使用上，并未对铣削时因下刀位置不同作路径规划优劣判断，本节针对平行多边形凹槽之往复式铣削，下刀位置（左或右向）不同，所造成之刀具路径差异作一探讨，并提出求最短路径步骤如下：

（1）从刀库中选择粗铣和精铣刀尺寸。

（2）画出沿凹槽边缘之刀具路径，形成一内多边形。

（3）从多边形中找出最小内角或内角与水平线夹角的角度。

（4）利用步骤（3）的结果求出刀具切削间距P及刀具平行切削道数。

（5）由内底边至顶点的高除以刀具切削间距，计算结果若为整数，即平行切削用实际道数，若非整数，则平行切削道数为取整数部分再加“1”。

（6）实际刀具切削间距，由底边至顶点的高除以平行切削实际道数，再由实际刀具切削间距除以粗铣刀具直径，得到真正刀具直径百分比。

（7）从刀具切削间距可得到真正粗铣刀具路径，再比较不同下刀位置所对应的以较短者为较佳的铣削路径。

以三角形凹槽铣削为例，如图1所示，其三内角为30、60、90度，内切圆角直径为10mm，三圆的圆心所构成三角形NOP为刀具路径经过路线，所经过路线（边长）越长则切削时间越长。以30°处为下刀起始点由右向左切削如图1所示，经ON边有三个路径间隔，经NP边也有三个路径间隔，或由60°处为下刀起始点由左向右切削如图2所示，经ON边有三个路径间隔，经NP边亦有三个路径间隔。由图1、图2可计算出两种情况的路径长。

现说明计算刀具实际切削路径间隔P′，经由上次所导出公式求出刀具切削间距P，刀具平行切削经过几道，由刀具切削间距P（刀具直径百分比）来决定。而刀具直径百分比系经三角形最小内角或与水平线最小之夹角所求出。计算方式如下：

假设H为三圆之圆心所构成三角形NOP之高，CD为三角形ABC之高。

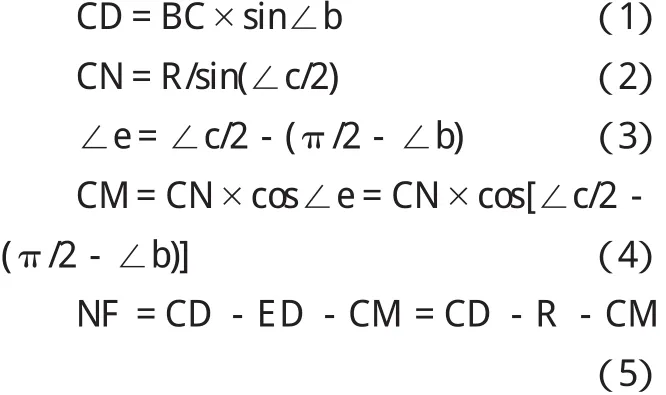
NF/P＝I＋J （I：整数 J：小数）

P′＝NF/(I＋1)

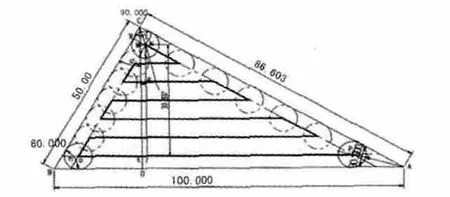
图1 三角形铣刀由右向左方向铣削

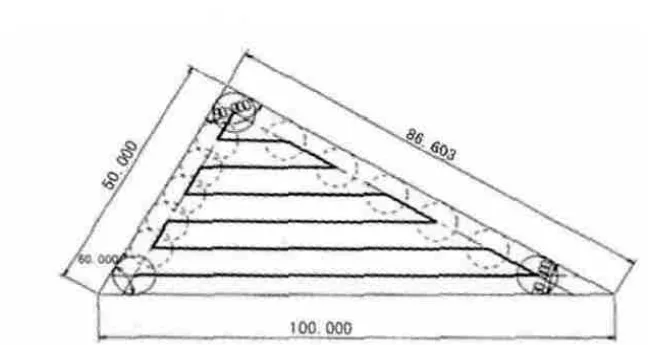
图2 三角形铣刀由左向右方向铣削

三角形图3、图4，计算说明如下：

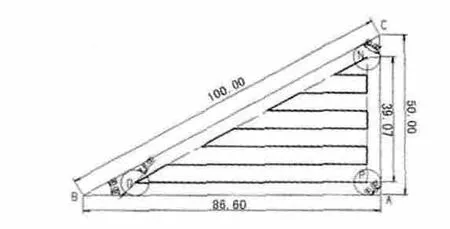
图3 三角形由右向左铣削刀具路径（边长86.6mm为底）

图4 三角形由左向右铣削刀具路径（边长86.6mm为底）

在图3、图4三角形中，NP为内三角形NOP的高

AC=BC×sin∠b

CN=R/sin(∠c/2)

NP=AC-R-cos(∠c/2)

h=Rsinθ P=h+R （θ：最小内角或与水平夹角）

NP/P=I+J （I：整数 J：小数）

P′=NP/(I+1)

此为MasterCAM软件双向平行切削刀具切削间距及刀具直径百分比之求法。从刀具切削间距可得到真正挖槽铣削刀具路径，由刀具路径来比较下刀位置，得到哪个切削路径较短，如此就可得到最佳铣削路径。