TNT 爆炸的数值计算及其影响因素

高轩能，吴彦捷

（华侨大学土木工程学院，福建 厦门361021）

引 言

炸药爆炸瞬时能释放巨大的能量并产生各种效应，但破坏力最强、影响区域最大的是爆炸冲击波。早期研究爆炸冲击波效应主要以实验为主，但因爆炸作用的时程极短，通常在数十毫秒内，爆炸冲击波即从最大值变为零，影响试验结果的准确性。近年来，随着计算机技术的快速发展，数值模拟方法已成为研究爆炸效应的重要手段。

爆炸空气冲击波超压计算常用方法有Sadovskyi公式、Henrych 公式、Brode公式，Aliansov公式 和TM5－1300表格等［1－4］。叶序双等［5］通过测量冲击波传播速度转换计算不同测点处的冲击波压力，对非理想刚性地面球形炸药爆炸冲击波超压进行实验研究并得到了大药量TNT 炸药在地面爆炸时的冲击波超压计算公式；仲倩等［6］通过爆炸试验测得空气冲击波峰值超压，对经验计算公式进行了系数修正；刘伟等［7－10］进行了TNT爆炸试验，并与有限元数值计算结果进行了对比研究，两者符合较好；杨鑫等［11］将数值计算结果与Henrych等冲击波超压经验公式进行了比较，指出数值计算结果普遍小于经验公式；李秀地等［12］在坑道爆炸试验数据的基础上，运用数值模拟方法研究了T 型坑道爆炸冲击波的传播衰减规律；卢红琴等［13－14］讨论了有限元网格密度和空气方程等参数变化对数值计算结果精度的影响。由此可见，现有研究主要集中在试验研究或数值计算，对引起爆炸数值模拟与经验计算公式结果之间误差程度不一的原因探讨较少。

本研究采用LS－DYNA 有限元程序建立TNT爆炸的数值计算模型，研究了空气冲击波的传播特性，结合经验公式和已有试验数据，验证计算模型及参数取值的可信性，分析探讨不同参数取值对冲击波超压的影响。

1 TNT 爆炸的数值计算

1．1 空爆计算模型的建立

应用LS－DYNA 有限元程序建立自由空爆模型。空气尺寸取12m×12m×12m 的较小空域，以节省运算时间，炸药尺寸取0．2m×0．2m×0．2m 的立方体，网格尺寸按0．1m×0．1m×0．1m 划分。空爆以炸药为中心取1／8模型计算，单元类型取8节点3D－SOLID164，采用ALE（Arbitrary Lagrange－Euler）算法。在XOY、XOZ、YOZ 平面内采用对称约束，其他面采用透射边界以模拟无限空气域。为考虑刚性地面对冲击波超压的影响，地面单元类型取为SHELL163，采用MAT＿RIGID刚体材料模型。

刚性地面具体参数为：＊MAT＿RIGID；3 7 830 2．07e30 0．300 0．00 0．00 0．00 0．00；1 7 7；0．00 0．00 0．00 0．00 0．00 0．00。

1．2 材料参数的选取

炸药和空气按均匀连续介质考虑。炸药采用MAT＿HIGH＿EXPLOSIVE＿BURN 材料模型和JWL（Jones－Wilkins－Lee）状态控制方程，爆炸冲击波压力为：

式中：A、B、R1、R2、ω 为输入参数；V 为相对体积；E0为初始内能。

TNT 的材料参数见表1。

表1 炸药的材料参数Tab 1 Material parameters of explosive

空气采用MAT＿NULL 空材料模型和线性多项式方程EOS＿LINEAR＿POLYNOMIAL，即：

式中：μ＝ρ／ρ0－1；E 为单位体积内能；ρ 为空气密度；ρ0为参考密度。

线性多项式状态方程遵守Gamma定律，空气的材料输入参数见表2。

表2 空气的材料参数Table 2 Material parameters of air

炸药在无限空气中发生爆炸时，爆炸波以炸药为圆心向四周传播，冲击波随着距离的增大能量逐渐耗散，超压峰值迅速衰减。自由空气爆炸冲击波在不同时刻的传播过程如图1所示。

1．3 数值计算结果与分析

1．3．1 数值计算结果的公式表达

基于上述建立的空中爆炸数学模型，为了研究更大范围内冲击波超压与比例距离的关系，模型中空气尺寸扩展为20m×20m×20m，网格尺寸取为0．2m×0．2m×0．2m，炸药仍为0．2m×0．2m×0．2m的立方体，同样取1／8模型计算。经过一系列数值计算，得到比例距离0．6～6．0m／kg1／3内的冲击波超压（见图2），以及1．0～3．0m／kg1／3内的正压作用时间（见图3）。经过拟合后，得到函数化表达的冲击波超压和正压作用时间计算公式分别如下：

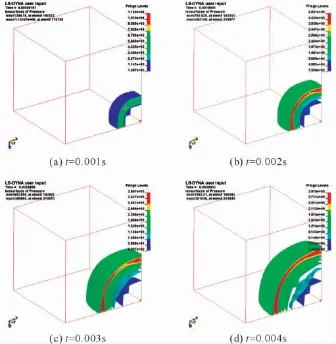
图1 空爆冲击波在不同时刻的传播图Fig．1 The spread process of the air explosion shock waves at different times

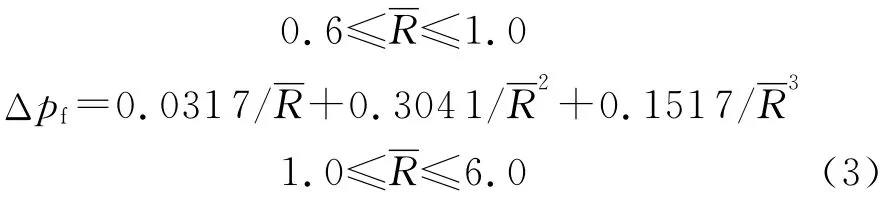
式中：Δpf为冲击波超压，MPa；，R 为 计算点到爆心的距离，m；m 为炸药药量，kg。

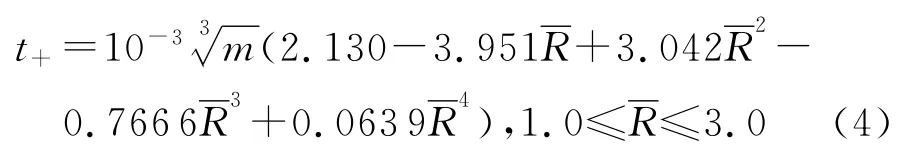
式中：t＋为正压作用时间，s。

1．3．2 数值计算结果与试验和经验公式计算值的比较

常用的空中爆炸冲击波超压（105Pa）经验公式见式（5）～（10）。

我国《爆破安全规程》GB6722－2003公式［15］：

Sadovskyi公式［1］：

Aliansov公式［4］：

常用的正压作用时间（s）经验公式有：

Henrych公式［2］：

Sadovskyi公式［1］：

式（10）中：B 取1．35［4］。

将冲击波超压数值计算结果与经验公式进行比较，结果见图2，图2中同时给出了拟合曲线（拟合曲线方程见式3）。

图2 由数值计算和经验公式得到的Δpf－R 曲线Fig．2 Δpf－curves obtained by the numerical calculation and empirical formulae

从图2可以看出，数值计算结果与经验公式计算值总体符合较好，而与Henrych 公式最为接近。随着比例距离的增大，数值计算结果与经验公式计算值的误差逐渐减小。

将正压作用时间数值计算结果与经验公式进行比较，结果见图3，图3 中同时给出了拟合曲线（拟合曲线方程见式4）。

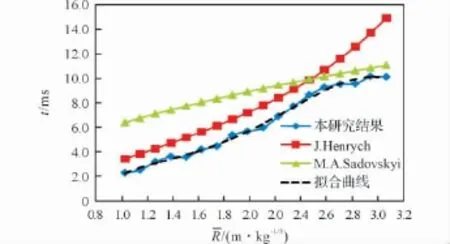
图3 正压作用时间数值计算与经验公式计算结果的比较Fig．3 Comparison of the results obtained by the positive pressure time numerical simulation with the empirical formula

为进一步验证数值计算结果的准确性，将相关文献中TNT 炸药爆炸试验的冲击波超压实测数据［16－20］、经验公式和数值计算结果进行比较，结果如图4所示。因爆心附近的参数测量较困难，爆炸试验实测的数据均在比例距离＝1．0～15．0m／kg1／3，因此，图4未给出小于1．0的值。

图4 TNT 爆炸试验数据、经验公式及数值计算结果的比较Fig．4 Comparison of the TNT explosion experimental data and the results obtained by empirical formula and numerical calculation

从图4可以看出，数值计算结果、试验结果和经验公式计算结果的变化趋势一致，随着比例距离的增大，三者的结果趋于相近，相互之间的误差越来越小。另一方面，不同试验结果或不同经验公式计算值之间也存在较大误差。例如，当为1．5m／kg1／3时，各经验公式的Δpf最大、最小和平均值分别为0．9138，0．1768 和0．4625MPa，最大值是最小值的5．2倍，试验所得Δpf的最大，最小和中间值分别为1．1107、0．0831和0．3279MPa，最大值是最小值的13．4倍，数值计算结果为0．2270MPa；由此可见，爆炸试验结果给出了冲击波超压的上位值（图中曲线幅宽的较大值）和中位值（平均值），Sadovskyi等经验公式得到中位值和下位值（图中曲线幅宽的较小值），数值计算则给出了下限值（最低值）。这是因为，在爆炸试验过程中，由于试验条件、测试范围的限制，以及地面或其他刚性物体产生的反射波效应，可能使冲击波超压得到增强，也使实测结果离散性较大。数值计算是基于理论状态方程建模，得到的是理想状态的爆炸效应，冲击波超压偏小是合理的。

通过TNT 爆炸数值计算，以及与经验公式计算值和试验数据的对比分析，验证了计算模型和参数取值的可信性。与试验结果相比，数值计算结果可以作为爆炸冲击波超压的下限值，而Henrych公式、Sadovskyi公式和我国《爆破安全规程》GB6722－2003公式给出的是中位值和下位值，存在低估爆炸冲击波超压的危险。

2 参数变化对冲击波超压的影响

2．1 炸药材料参数的影响

本研究从文献中按TNT 的不同材料参数取值，给出具有代表性的3组，如表3所示，分别进行数值计算。炸药尺寸仍为0．2m×0．2m×0．2m，空气尺寸为8m×8m×8m，取1／8模型计算。对表3材料代表值进行计算，结果见表4。

从表4可以看出，第3 组与第1 组的计算结果基本相同，在比例距离＝0．45～1．65m／kg1／3范围内，两者误差的绝对值不超过4%；第2组计算结果比第1 组和第3 组均小，比例距离小 于1．05m／kg1／3时，相 对 误 差 的 绝 对 值 超 过10%，但随着比例距离的增大，差值逐渐减小，比例 距 离大 于1．05m／kg1／3后，第2 组 与 第1 组的超压相对误差绝对值不超过8%。表明随着比例距离的增大，3组材料参数取值的数值计算结果逐渐趋同。

表3 TNT 的不同材料参数Table 3 Different material parameters of TNT

表4 不同材料参数下的冲击波超压Table 4 The shock waves overpressure under different material parameters

2．2 TNT 药量的影响

TNT爆炸的数值计算模型：空气尺寸为10m×10m×10m，炸药尺寸分别为0．2m×0．2m×0．2m、0．3m×0．3m×0．3m、0．4m×0．4m×0．4m 和0．5m×0．5m×0．5m，即TNT 药量分别为13．04、44．01、104．32和203．75kg组，取1／8模型计算，计算结果见表5。从表5可以看出，相同比例距离下，当TNT 药量从13．04kg增加到203．75kg时，虽然药量增加了14．625倍，但相应的冲击波超压增减没有超过20%，呈比较平稳增加的状态。表明在同等条件下，TNT 药量的增减不会显著影响TNT 爆炸的数值计算结果，仅会引起冲击波超压的小幅度增减。

表5 不同TNT 药量下冲击波超压的数值计算结果Table 5 The numerical calculation results of shock wave overpressure under different TNT dosage

2．3 单元网格划分的影响

为探讨网格划分密度对数值计算结果的影响，分别按0．1、0．2、0．3和0．4m 的网格尺寸划分单元。空气尺寸为12m×12m×12m，炸药取0．1m×0．1m×0．1m 的立方体，取1／8 模型计算，计算结果如图5所示。

从图5可看出，网格划分密度对数值计算结果的影响程度取决于比例距离。当比例距离小于2．0m／kg1／3时，网格尺寸对计算精度有较大影响，例如，当比例距 离 为1．44m／kg1／3时，Henrych 公 式 的Δpf为0．344MPa，按0．1、0．2、0．3和0．4m 网格密度计算得到的Δpf分别为0．305、0．259、0．220和0．208MPa，与Henrych公式计算结果的误差分别为－11．4%、－24．8%、－36．1%和－39．6%，误差增大了28．2%，表明加密单元网格可以有效提高爆炸模拟计算的精度。随着比例距离的增大，网格划分密度对计算结果的影响逐渐减小。当比例距离为5．0m／kg1／3时，按不同网格划分密度计算的结果，相对误差小于2．5%，网格划分密度对超压的影响可以忽略不计。

图5 不同单元网格划分下的Δpf－ 曲线Fig．5 Δpf－curves under different mesh sizes

2．4 建模方式的影响

考虑两种模型：空气尺寸8m×8m×8m、立方体炸药0．2m×0．2m×0．2m 的1／8模型和空气尺寸16m×16m×16m、立方体炸药0．4m×0．4m×0．4m 的整体模型。为考察建模方式对爆炸冲击波空间分布的影响，分别提取Z＝0平面（水平面）和对角线平面（斜平面）上不同比例距离的冲击波超压数值计算结果进行对比，见表6。

由表6可知，相同比例距离下，整体模型数值计算的冲击波超压一般是1／8模型的1．03～1．25倍，多数计算点误差在10%内，仅少数计算点误差超过20%，但与比例距离没有呈现明显的规律性。主要原因在于爆炸荷载是动态荷载，取1／8模型进行计算时，有可能无法计算部分反射波的增强效应。

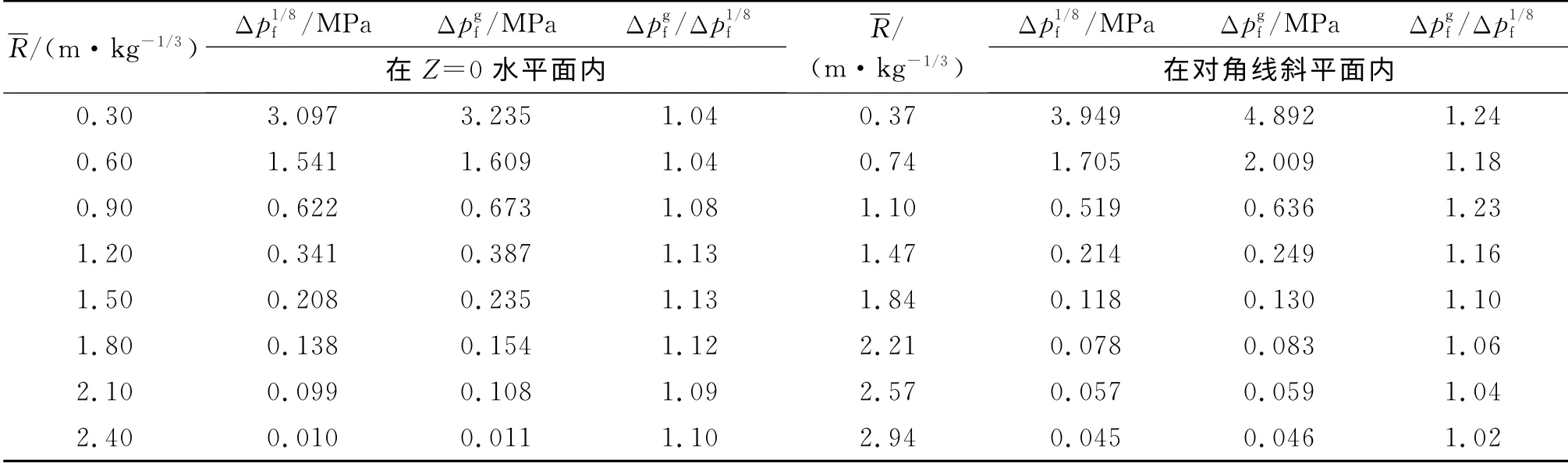
表6 不同建模方式下冲击波超压的数值计算结果Table 6 The numerical calculation results shock wave overpressure under different modeling ways

2．5 空气域形状的影响

分别建立立方体（边长12m）、圆柱体（半径12m、径高比1∶1）和球体（半径12m）3 种不同空气域的1／8模型，TNT 均为0．1m×0．1m×0．1m的立方体，数值计算结果如图6所示。从图6可以看出，3种不同空气域形状对爆炸冲击波超压的影响很小，立方体空气域计算结果稍大些，也更符合经验公式。

图6 不同空气域形状下的Δpf－ 曲线Fig．6 Δpf－curves under different air domain shapes

2．6 炸药形状的影响

分别建立立方体、圆柱体（径高比1∶1）和球形体TNT 在立方体空气域内的1／8爆炸模型，TNT药量分别为104．32、109．00和106．63kg，以便于网格划分，药量之差小于5%，其对超压的影响可以忽略不计，数值计算结果如图7所示。

图7 不同TNT 形状的Δpf－曲线Fig．7 Δpf－curves with different shapes of TNT

从图7可以看出，与网格划分密度的影响类似，炸药形状对数值计算结果的影响程度取决于比例距离 的 大 小。比 例 距 离小 于1．5m／kg1／3时，TNT 形状对冲击波超压的影响较大，此时，在相同的比例距离下，圆柱体TNT 得到的冲击波超压最大，球形体次之，立方体最小。比例距离大于1．5m／kg1／3后，TNT 形状对计算结果的影响很小，可以忽略不计。

3 结 论

（1）基于LS－DYNA 有限元程序实现TNT 爆炸冲击波超压及正压作用时间的数值计算是可行的。数值计算结果可以作为爆炸冲击波超压的下限值。

（2）与试验数据相比，用Henrych 公式、Sadovskyi公式和我国《爆破安全规程》GB6722－2003公式计算冲击波超压给出的是中位值和下位值，存在低估冲击波超压的危险。

（3）建模方式和空气域形状对TNT 爆炸数值计算结果的影响可以忽略不计。在相同比例距离下，数值计算的冲击波超压随TNT 药量的增加有小幅度增加。

（4）材料参数取值、单元网格密度和TNT 形状对数值计算结果的影响与比例距离密切相关。在比例距离较小的范围内（如小于2．0m／kg1／3或更小）进行数值计算时，不能忽视网格划分密度、TNT形状和材料参数取值对计算结果的影响。

［1］ Sadovskyi M A．Mechanical Action of Air Shock Waves of Explosion，Based on Experimental Data［M］．Moscow：Izd Akad Nauk SSSR，1952．

［2］ 亨利奇．J．爆炸动力学及其应用［M］．熊建国，译．北京：科学出版社，1987．

［3］ Brode H L．Blast wave from a spherical charge［J］．The Physics of Fluids，1959，2（2）：217－229．

［4］ 李翼祺，马素贞．爆炸力学［M］．北京：科学出版社，1992．

［5］ 叶序双，戴镇华，庄兆铃．非理想刚性地面球形装药爆炸冲击波超压的试验研究［J］．解放军理工大学学报（自然科学版），1988（4）：72－82．YE Xu－shuang，DAI Zhen－hua，ZHUANG Zhao－ling．Study on the ideal rigid ground ball shape explosion shock wave overpressure experiments［J］．Journal of PLA University of Science and Technology（Natural Science Edition），1988（4）：72－82．

［6］ 仲倩，王伯良，黄菊，等．TNT 空中爆炸超压的相似律［J］．火炸药学报，2008，33（4）：32－35．ZHONG Qian，WANG Bo－liang，HUANG Ju，et al．Study on the similarity law of TNT explosion overpressure in air［J］．Chinese Journal of Explosives and Propellants，2008，33（4）：32－35．

［7］ 刘伟，郑毅，秦飞．近地面TNT 爆炸的试验研究和数值模拟［J］．爆破，2012，29（1）：5－9．LIU Wei，ZHENG Yi，QIN Fei．Experimental and numerical simulation of TNT explosion on the ground［J］．Blasting，2012，29（1）：5－9．

［8］ 周保顺，张立恒，王少龙，等．TNT 炸药爆炸冲击波的数值模拟与实验研究［J］．弹箭与制导学报，2010，30（3）：88－90．ZHOU Bao－shun，ZHANG Li－heng，WANG Shaolong，et al．Numerical simulation and experimental research on TNT explosion shock wave［J］．Journal of Projectiles，Rockets，Missiles and Guidance，2010，30（3）：88－90．

［9］ 李加贵，边小华，张雷．爆炸冲击波传播的数值模拟与试验数据对比［J］．山西建筑，2006，32（8）：106－107．LI Jia－gui，BIAN Xiao－hua，ZHANG Lei．Numerical simulation of blast wave propagation in tunnel compared with experiment data［J］．Shanxi Architecture，2006，32（8）：106－107．

［10］张广福，刘玉存，王建华．爆炸冲击波无限空气领域传播的数值模拟研究［J］．山 西化工，2009，29（1）：43－46．ZHANG Guang－fu，LIU Yu－cun，WANG Jian－hua．Numerical simulation study on propagation of shock wave in the air without obstacles［J］．Shanxi Chemical Industry，2009，29（1）：43－46．

［11］杨鑫，石少卿，程鹏飞．空气中TNT 爆炸冲击波超压峰值的预测及数值模 拟［J］．爆破，2008，25（1）：15－19．YANG Xin，SHI Shao－qing，CHENG Peng－fei．Forecast and simulation of peak overpressure of TNT explosion shock wave in the air［J］．Blasting，2008，25（1）：15－19．

［12］李秀地．T 型坑道中爆炸冲击波传播规律的数值模拟［J］．后勤工程学院学报，2011，27（4）：8－12．LI Xiu－di．Numerical simulation for blast propagation and attenuation inside T－shaped tunnel from hecharges detonation［J］．Journal of Logistical Engineering University，2007，30（4）：55－57．

［13］卢红琴，刘伟庆．空中爆炸冲击波的数值模拟研究［J］．武汉理工大学学报，2009，31（19）：105－108．LU Hong－qin，LIU Wei－qing．Research on numerical simulation of blast wave in air［J］．Journal of Wuhan University of Technology，2009，31（19）：105－108．

［14］石磊，杜修力，樊鑫．爆炸冲击波数值计算网格划分方法研究［J］．北京工业大学学报，2010，36（11）：1465－1470．SHI Lei，DU Xiu－li，FAN Xin．A study on the mesh generation method for numerical simulation of blast wave［J］．Journal of Beijing University of Technology，2010，36（11）：1465－1470．

［15］GB6722－2003 爆破安全规程［S］．北京：中国工程爆破协会，2003．

［16］张陶，惠君明，解立峰，等．FAE 爆炸场超压与威力的实验研究［J］．爆炸与冲击，2004，24（2）：176－181．ZHANG Tao，HUI Jun－ming，XIE Li－feng，et al．Experimental research on the overpressure and power in the FAE blast field［J］．Explosion Shock Waves，2004，24（2）：176－181．

［17］董桂旭，杜茂华，黄雪峰．某型炸药的冲击波超压峰值计算公式参数的修正［J］．海军航空工程学院学报，2010，25（5）：542－544．DONG Gui－xu，DU Mao－hua，HUANG Xue－feng．Correction on parameters of calculation formula for shockwave overpressure peak value of one explosive［J］．Journal of Naval Aeronautical and Astronautical University，2010，25（5）：542－544．

［18］胡华权，裴明敬，许学忠，等．燃料空气炸药爆炸威力评价方法研究［C］∥第四届全国爆炸力学实验技术学术会议论文．合肥：安徽省力学学会，2006：313－318．HU Hua－quan，PEI Ming－jing，XU Xue－zhong，et al．Study on the evaluation method of fuel－air explosive power［C］∥The Fourth Session of the National Explosion Mechanics Experiment Technology of Academic Debate．Hefei：Anhui Society of Theoretical and Applied Mechanics，2006：313－318．

［19］郭炜，俞统昌，金朋刚．三波点的测量与实验技术研究［J］．火炸药学报，2007，30（4）：55－57．GUO Wei，YU Tong－chang，JIN Peng－gang．Test of triple point and study on its test technology［J］．Chinese Journal of Explosives and Propellants，2007，30（4）：55－57．

［20］王建灵，郭炜，冯晓军．TNT、PBX 和Hexel空中爆炸冲击波参数的实验研究［J］．火炸药学报，2008，31（6）：42－44．WANG Jian－ling，GUO Wei，FENG Xiao－jun．Experimental research on the air explosion shock wave parameters of TNT，PBX and Hexel［J］．Chinese Journal of Explosives and Propellants，2008，31（6）：42－44．

［21］高轩能，王书鹏．大空间柱壳结构爆炸动力响应的Ritz－POD数值模拟［J］．土木建筑与环境工程，2010，32（2）：64－70．GAO Xuan－neng，WANG Shu－peng．Numerical simulation for dynamic response of large－space cylindrical reticulated shell under internal explosion by Ritz－POD method［J］．Journal of Civil，Architectural and Environmental Engineering，2010，32（2）：64－70．

［22］姜宏，刘鹏．爆炸荷载作用下钢框架动力响应有限元分析［J］．湖南科技大学学报（自然科学版），2010，25（2）：55－58．JIANG Hong，LIU Peng．Fea dynamic analysis of steel frame under explosive load［J］．Journal of Hunan University of Science and Technology（Natural Science Edition），2010，25（2）：55－58．

［23］田志敏，邬玉斌，罗奇峰．隧道内爆炸冲击波传播特性及爆炸荷载分布规律研究［J］．振动与冲击，2011，30（1）：21－26．TIAN Zhi－min，WU Yu－bin，LUO Qi－feng．Characteristics of in－tunnel explosion－induced air shockwave and distribution law of reflected shock wave load［J］．Journal of Vibration and Shock，2011，30（1）：21－26．

［24］Katayama M，Kibe S，Yamamoto T．Numerical and experimental study on the shaped charge for space debris assessment［J］．Acta Astronauttca，2001，48（5－12）：363－372．

［25］廖维张，杜修力，田志敏．爆炸荷载作用下部分埋置结构响应的数值模拟方法［J］．北京工业大学学报，2007，33（2）：155－159．LIAO Wei－Zhang，DU Xiu－li，TIAN Zhi－min．Numerical simulation methods on dynamic response of partially buried structure under blast loading［J］．Journal of Beijing University of Technology，2007，33（2）：155－159．

［26］尚晓江．ANSYS／LS－DYNA 动力分析方法与工程实例［M］．北京：中国水利水电出版社，2005．