基于改进RBF神经网络的钢构件质量预测研究

雷兆明 ，王东泽 ，花季伟 ，王 军

（1.河北工业大学 控制科学与工程学院，天津 300130；2.天津师范大学 计算机与信息工程学院，天津 300387）

近年来，随着国民经济的显著提高，人们生活节奏加快，社会对桥梁、道路、商场、车站等基础设施建设有了更高的要求，以钢结构为主体的钢结构建筑体系应用得到快速发展，其速度快、安全性高的特点得到了社会各界的广泛认可[1]。质量问题是企业生产过程中最为重要的环节，因此，设计合理高效的产品质量预测系统，研究产品的质量预测问题，对于寻找生产过程中最优工艺参数，为在生产过程中实现最优控制有着重要作用。

一个完善的质量预测系统，应用生产过程中采集的大量数据进行质量预测，随着现代化生产线快速发展，对这些数据的采集愈加完善和准确，如何高效利用这些数据，进行更加准确的质量预测，保证产品质量控制在理想的范围内，是目前现代质量控制的重点发展方向。然而，影响产品质量的工艺参数有很多，而且他们与产品质量的关系一般存在着复杂的非线性和强耦合关系，人工神经网络能模拟实现复杂的输入输出关系，适合解决非线性和不确定性高的问题。

1 改进RBF神经网络算法

1.1 RBF神经网络的学习

目前，径向基函数 RBF（radial basis function）神经网络算法在质量预测领域得到了广泛的应用[2]，RBF神经网络拥有强大的自学习能力，使它在应对复杂多变的生产过程中的工艺参数时，有很强的适用性；同时它的高度并行处理能力，使它在质量预测系统中，拥有很高的信息处理速度[3]。但是随着广大科研人员对RBF神经网络研究的愈加深入和在众多系统应用中得到检验，一些不足之处渐渐显露出来，容易陷入局部极小值、收敛速度较慢和隐含层节点数目难以确定。针对上述缺点，采用相应的方式对其进行改进，使其在实际应用中达到更为理想的效果。

RBF神经网络学习参数有3个：基函数中心、宽度（方差）和输出权值。其中基函数中心和宽度直接影响输入层到隐含层之间的空间映射结构，所以他们的选择是重中之重。

一般可以通过3种方法来确定基函数中心，直接法、自组织学习法和有监督学习法[4]。直接法就是根据经验和样本特点直接确定；自组织学习法就是采用聚类方法，通常利用K-均值聚类把样本聚成M类，这样RBF的中心就选取类的中心；有监督学习法是让3个参数通过监督学习后再确定，通过修正误差一点点来优化参数。

然后，通常会用固定法来确定基函数的宽度，例如，当RBF神经网络基函数采用高斯函数时，其方差为

式中：dmax为基函数各中心之间的最大距离；Nh为隐含层单元数量。

固定了基函数中心和宽度之后，输入层到隐含层的空间结构就固定了，这时可以把网络等效成一个单层网络，并且是带有线性输出的，通常采用最小二乘法求权值。

1.2 遗传算法的研究

遗传算法是一种智能搜索算法，是在上世纪七十年代被美国学者John Holland提出的[5]，如图1所示为遗传算法的工作流程图，通过观察，可以发现遗传算法就是通过迭代运行进行求解，具体运算流程如下：

①把要解决的问题参数集映射到合适的染色体编码空间；

②设定适应度函数；

③设计选择、交叉、变异等算子，然后再确定种群规模N、交叉概率和变异概率的遗传算法参数；

④假设t=0，任意的生成N个初始个体得到种群 P（0）；

⑤评价P（t）中各个个体的适配值；

⑥判断新种群能否终止算法，如果不能就继续执行算法，能的话就直接输出适配值最高的个体；

⑦得到新一代种群P（t+1），即把之前设计的选择、交叉和变异算子作用于种群；

⑧用产生的新种群 P（t+1）代替原来的 P（t），再返回⑤继续执行。

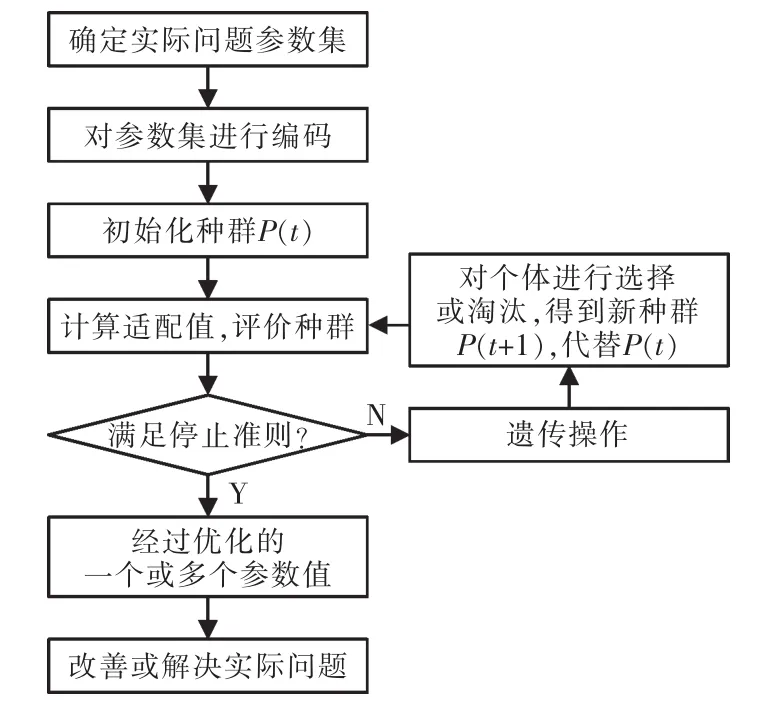
图1 遗传算法工作流程示意Fig.1 Genetic algorithm work flow chart

1.3 遗传算法改进RBF神经网络算法

由于遗传算法具有搜索全局最优解的能力，而上面提到基函数中心和宽度对RBF神经网络很重要，利用遗传算法来优化RBF神经网络的参数，可以避免局部最优的情况，所以采用遗传算法来优化RBF神经网络隐含层的基函数中心cj、宽度σj和权值 ωi[6]。

根据上文提到的遗传算法寻优过程，具体操作如下：

1）编码操作

在编码时，把基函数中心cj、宽度σj和权值ωi放在同一条染色体上，使σj和cj交替排列，权值ωi的编码放在染色体末端。设输入节点数为m、隐含节点数为p、输出节点数为n，染色体长度为l，则

染色体的结构如图2所示。

图2 染色体编码示意Fig.2 Chromosome coding schemes graph

2）适应度函数的构造

遗传算法中适应度函数是对个体评价的主要指标，进行优化时，将目标函数转化为适应度函数，让目标函数和适应度函数有着一致的优化方向，这样适应度最大时目标函数也会达到最大。训练RBF神经网络时，希望输出与参考输出之间误差尽量小，将第i个个体适应度函数表示如下：

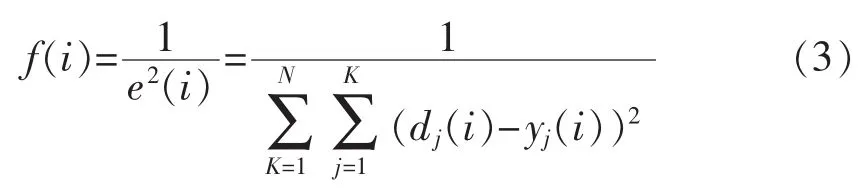
式中：dj（·）表示第 j个输出节点的参考输出；yj（·）表示第j个节点的实际输出；N为训练的样本数量；K为输出节点数。

3）种群初始化

本文对RBF神经网络的基函数中心cj、宽度σj和权值ωi进行初始化。在遗传过程中，一般的操作都是对初始种群的基因进行的，通常基因范围不会超出原始基因，所以在遗传算法寻优时种群初始化非常重要。

根据经验，选取60作为种群数量，基因的初始化一般采用随机数生成，让基函数中心cj和宽度 σj在［-15，15］区间生成，权重 ωi在［-1，1］区间生成。

4）选择操作

作为种群进化的核心，它决定父代种群中的个体能否遗传到下一代中，本文选择遗传算法里面常用的适应度比例方法。

设个体数为N，其中个体xi的适应度为fi，pi为个体被选择的概率，则有

选择时，在区间［0，1］选一个随机数 r，当 r满足下式时，则第j个个体被选择。

5）交叉

交叉操作分为单点和多点，单点交叉操作如图3所示。

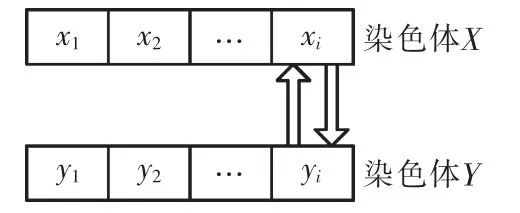
图3 交叉操作示意图Fig.3 Crossover operation schematic

式中，0＜α＜1，一般情况下α取随机数或交叉概率。

6）变异

在以实数编码的染色体中，通过变异可以得到定义空间的任何值，由于生物的基因变异具有方向不确定的特点，在应用时，采用随机数来处理。变异时，先随机选择一条染色体 X=｛x1，x2，x3，…，xk，…，xn｝，再利用随机数选择变异基因xk，设基因xk的定义域是［xkmin，xkmax］。 然后在（0，1）区间内生成一个随机数β，则变异后的基因xk′如下式，最后用新基因xk′替换基因xk，从而形成新的染色体。

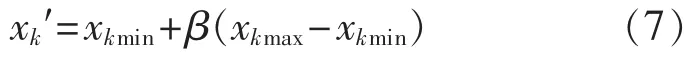
进行交叉时，先生成一个随机数，在随机数所对应染色体位置进行交叉变异。由于采用了实数编码，因此定义交叉后基因式如下：

2 质量预测的仿真与结果分析

2.1 仿真中输入输出的选择

在大型钢构件加工生产过程中，焊接是影响产品质量最为重要的工序，焊接质量更会直接影响整个构件甚至整个工程的质量。本文以河北某个大型钢构件制造业为背景，以质量问题和焊接过程中的工艺参数作为RBF神经网络的输入，造成质量问题的原因作为输出，质量问题包括咬边、飞溅、夹渣、弧坑裂纹、接头不良、气孔6个主要问题，工艺参数包括电流、电压、CO2流量、焊接速度、装配间隙、焊条直径和焊件厚度，输出为造成质量问题原因编码。质量问题的编码如表1所示，输入对应如表2所示，输出位对应编码如表3所示。

表1 质量问题编码表Tab.1 Quality problem code table

表2 输入变量对应表Tab.2 Table of input variables

表3 输出位对应编码表Tab.3 Coding schedule of output bit

2.2 仿真结果与分析

本文中选取30组从实际生产中采集的数据进行仿真，如表4所示，仿真过程中隐含层节点数为20，训练误差精度为10-2。

表4 样本数据Tab.4 Table of sample data

采用RBF神经网络进行仿真，得到的仿真结果如图4所示，从结果中可以看出，训练没有达到要求的精度，训练200次以后，系统误差不再减少，即陷入局部最优，因此需要改进RBF神经网络算法。

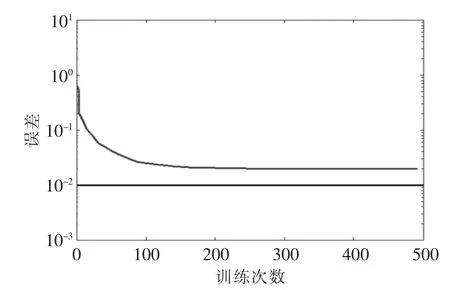
图4 样本训练误差与进化次数仿真结果（RBF）Fig.4 Samples training error and the number of evolution simulation result

用遗传算法改进RBF神经网络之后，得到如图5所示的仿真结果，从中发现误差随着训练次数快速下降，能够达到10-2以下。

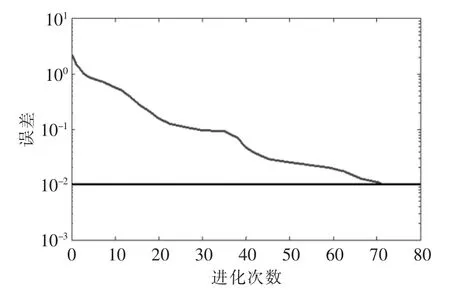
图5 样本训练误差与进化次数仿真结果（改进RBF）Fig.5 Samples training error and the number of evolution simulation result

用样本｛5，420，36，18，1.2，1，1.6，6｝对训练后的RBF进行验证，系统输出为｛0.0023，-0.0016，-0.0011，1.0027，0.0039｝，经过取整后为｛0，0，0，1，0｝，转化为质量问题原因后是焊接速度过大，诊断结果符合实际情况。以此方法一共用5组样本对训练后的RBF神经网络进行验证，得到验证结果均与实际结果相符，验证结果如表5所示。

表5 样本验证结果Tab.5 Table of sample test results

3 结语

针对大型钢构件生产过程中的质量问题，本文采用改进RBF神经网络进行预测，RBF神经网络本身具有强大的学习能力和适用性，采用遗传算法对其进行改进，优化了RBF神经网络主要参数的选择，相比较于其他算法，遗传算法更可避免其陷入局部最优。最后，通过仿真证明，该方法应用在实际质量预测中是有效的，在实际生产中可得到推广。

[1]贺海勃.浅议钢构件加工质量控制[J].中国建筑金属结构，2013（8）：77-79.

[2]雷琪，刘君贤，何勇，等.基于PCA与RBF的焦炭质量预测模型[J].控制工程，2010，17（4）：513-516，520.

[3]Han H G，Chen Q，Qiao J F.An efficient self-organizing RBF neural network for water quality prediction[J].Neural Networks，2011，24（7）：717-725.

[4]Schubert M，Muffler A，Mourad S.The use of a radial basis neural network and genetic algorithm for improving the efficiency of laccase-mediated dye decolourization[J].Journal of Biotechnology，2012，161（4）：429-436.

[5]辛若波.基于遗传优化和贝叶斯正规化神经网络的空气质量预测研究[D].山东：山东大学，2013.

[6]李宝栋，宿忠娥，吴晓红，等.基于GA-RBF神经网络的电火花成形加工电参数优化[J].工业仪表与自动化装置，2013（2）：87-89.