基于间接Radau伪谱法的滑翔段轨迹跟踪制导律

廖宇新，李惠峰，包为民，2

(1．北京航空航天大学宇航学院，北京100191;2．中国航天科技集团公司科技委，北京100048)

0 引言

在滑翔段飞行过程中，制导系统承担着引导高超声速飞行器在不违背各种约束的前提下准确到达目标这一至关重要的作用。因此，研究具有鲁棒性和实时性的滑翔段制导律意义重大。

按照制导策略通常将滑翔段制导律分为预测校正制导［1－3］和标称轨迹跟踪制导［4－10］。预测校正制导是根据飞行器当前的真实状态对轨迹进行快速预测，得到终端状态量，然后根据所得结果与终端约束条件的偏差值对控制量进行校正。预测校正制导不需要存储标称轨迹，能适应更大范围的偏差和扰动。但是，数值预测校正制导对弹载计算机的计算能力要求很高，难以满足实时性的需求，且不能保证收敛的可行解的存在;而解析预测校正制导所用的模型都经过了简化处理，解的预测精度和对飞行任务的适应能力均不理想。

标称轨迹跟踪制导主要包括标称轨迹生成和轨迹在线跟踪两部分。为了提高标称轨迹跟踪制导的自主性、自适应性和鲁棒性，对于现有方法的改进主要沿着两条技术路线展开:一是研究轨迹在线生成算法，二是研究能够在线实时解算且具有鲁棒性和自适应性的标称轨迹跟踪方法［4］。文献［5］以高度、速度、航迹倾角的变化曲线作为标称轨迹，对降阶的运动方程组进行线性化，将二维平面轨迹跟踪问题转化为线性时变(Linear Time-Varying，LTV)系统状态调节器问题来求解，但基于系数冻结法的在线增益调参技术在处理LTV系统状态调节器问题时存在费时、鲁棒性差、稳定性无理论保证等不足。文献［6］通过求解Riccati矩阵微分方程来求解航天飞机三维平面标称轨迹跟踪问题转化得到的LTV系统状态调节器问题，但在线求解Riccati矩阵微分方程也存在费时、数值不稳定等不足［8］。文献［7］将三维平面标称轨迹跟踪问题转化为LTV系统滚动时域控制问题，为避免求解Riccati矩阵微分方程的数值计算负担，将LTV系统滚动时域控制问题离散化，近似转化为二次规划(Quadratic Programming，QP)问题来求解，并证明了闭环系统的稳定性。文献［7］的方法具有很强的鲁棒性，但当离散的阶次较高时，推导和计算都比较复杂。文献［11］利用间接Legendre伪谱法(Indirect Legendre Pseudospectral Method，ILPM)求解LTV系统状态调节器问题转化得到的线性两点边值问题(Two Point Boundary Value Problem，TPBVP)，不存在求解Riccati矩阵微分方程和在线增益调参的过程。文献［4，8－10］结合相关策略进一步研究了基于ILPM的高超声速飞行器滑翔段轨迹跟踪制导律，验证了制导律的鲁棒性和实时性。

本文提出了间接Radau伪谱法(Indirect Radau Pseudospectral Method，IRPM)来求解LTV系统状态调节器问题转化得到的线性TPBVP。文献［11］中，线性TPBVP经过ILPM离散转化后，得到的是超定线性方程组，只存在最小二乘解。本文与文献［11］不同的是，线性TPBVP经过IRPM离散转化后，得到的是适定线性方程组，能求得唯一的精确解。基于IRPM求解得到的最优反馈控制律，提出了一种滑翔段全状态标称轨迹跟踪制导律。该制导律具有良好的鲁棒性和在线执行的能力。

1 标称轨迹跟踪制导问题的转化

假设地球为自转圆球，高超声速飞行器滑翔段无动力飞行的三自由度运动方程组参考文献［3］。飞行器的状态量x=［r，θ，φ，V，γ，ψ］，分别为地心矢径、经度、纬度、速度、航迹倾角、航迹偏角;控制量u=［α，σ］，分别为攻角和倾侧角。

实际飞行轨迹与标称轨迹之间存在偏差，其中状态量偏差量为 δx(t)∈Rn，控制量偏差量为δu(t)∈Rm。基于标称轨迹(xr，ur)对运动方程组进行线性化，得到LTV系统的状态方程和初始条件分别为

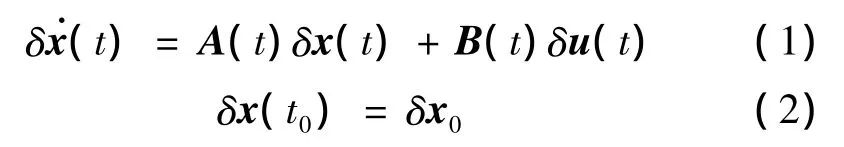
进一步考虑如下的二次型性能指标

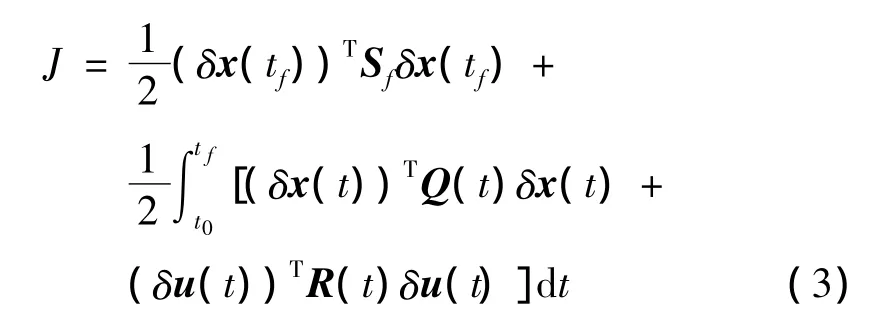
式中:Sf∈Rn×n和Q(t)∈Rn×n是对称半正定矩阵，R(t)∈Rm×m是对称正定矩阵。标称轨迹跟踪制导问题可以转化为LTV系统状态调节器问题:确定最优反馈控制律 δu*(δx*，t)，在满足式(1)、(2)所示约束的前提下，使式(3)所示性能指标函数取最小值。

令哈密尔顿函数为

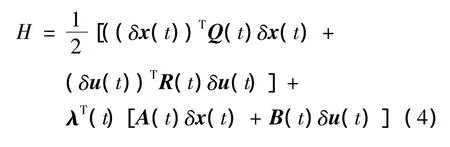
式中:λ(t)∈Rn为协态变量。由Pontryagin极大值原理可得线性TPBVP为

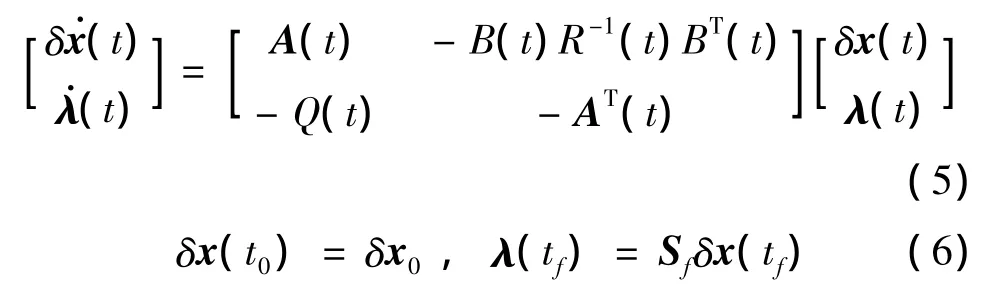
一阶最优必要条件为

进一步可得最优反馈控制律为

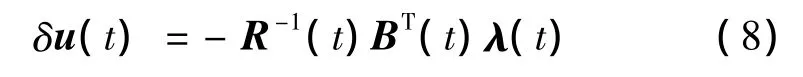
由此可知，通过求解上述线性TPBVP，获得协态变量 λ(t)，即可得到最优反馈控制律 δu*(δx*，t)。

2 基于间接Radau伪谱法的最优反馈控制律

为了避免后向扫描法中反向积分Riccati矩阵微分方程时的数值敏感性，以及转换矩阵法中可能产生病态转换矩阵导致数值计算不稳定的问题［8］，同时满足实时计算最优反馈控制律的需求，本文采用间接Radau伪谱法来求解上述线性TPBVP，进而获得最优反馈控制律。

由于Legendre-Gauss-Radau(LGR)点 τk∈［－1，1)，首先需要将时间区间t∈［t0，tf］通过式(9)转换到［－1，1］

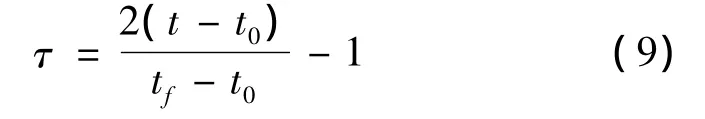
时间区间转换后的线性TPBVP为

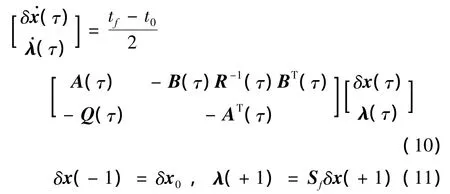
以N个LGR点τk和终端时刻点τf=τN+1=+1为节点，利用Lagrange插值方法对状态量偏差量δx(τ)和协态变量λ(τ)进行近似

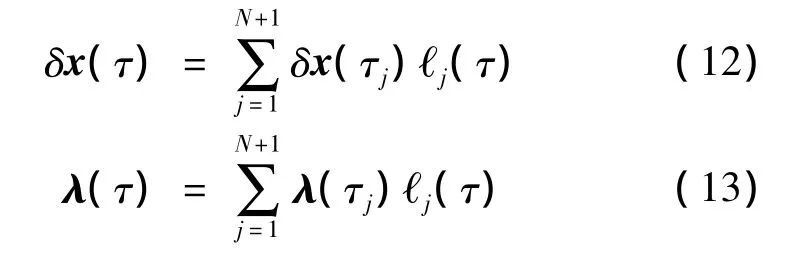
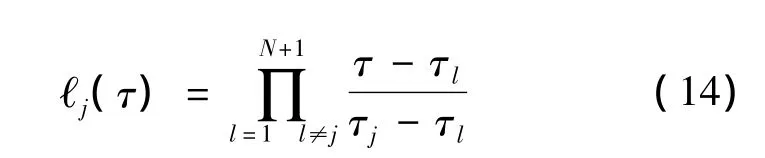
式中:τj∈［－1，1］为插值节点，ℓj(τ)为Lagrange插值基函数。由此可得，状态量偏差量和协态变量关于变换后时间的导数在LGR点处的值分别为

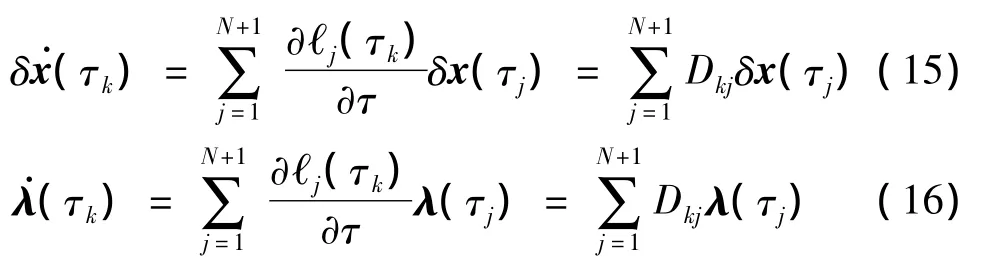
将式(15)、(16)代入式(10)，线性TPBVP中的微分方程组转化为如下的代数方程组

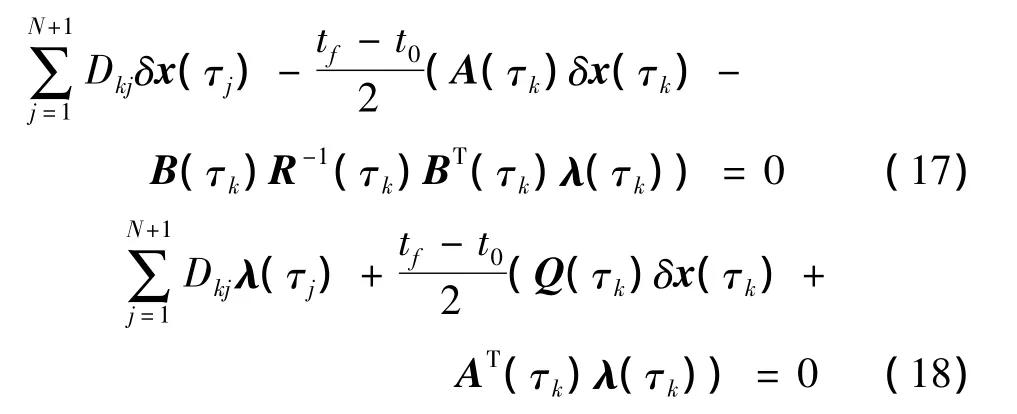
令δx=［(δx(τ1))T，(δx(τ2))T，…，(δx(τN+1))T］T，λ=［λT(τ1)，λT(τ2)，…，λT(τN+1)］T，Ze=［(δx(τ2))T，…，(δx(τN+1))T，λT(τ1)，…，λT(τN+1)］T，Z=［(δx)T，λT］T=，综合式(11)、(17)、(18)并写成如下式所示的分块的形式

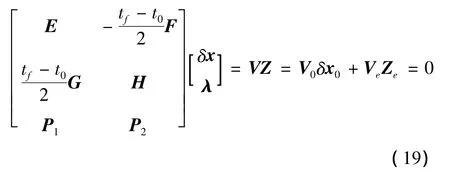
式中:E、F、G、H∈RNn×(N+1)n，Z∈R(2N+2)n×1，V∈R(2N+1)n×(2N+2)n，P1=［0n×n，…，0n×n，Sf］ ∈Rn×(N+1)n，P2=［0n×n，…，0n×n，－In×n］∈Rn×(N+1)n，δx0∈Rn×1，V0∈R(2N+1)n×n，Ze∈R(2N+1)n×1，Ve∈R(2N+1)n×(2N+1)n，

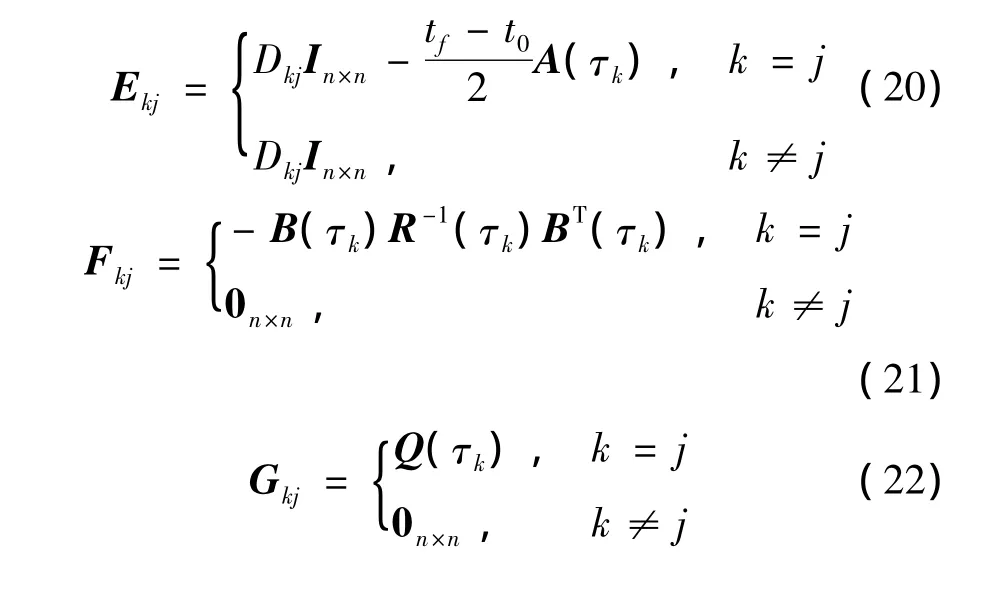
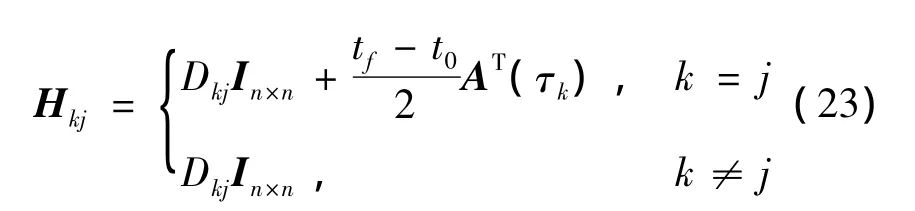
式(19)中有(2N+1)n个方程，对应于(2N+1)n个未知数，这表明VeZe=－V0δx0是适定线性方程组。由文献［10］可知，矩阵V是列满秩的，且可分解为矩阵V0和方阵Ve，所以Ve是列满秩的方阵。因此，可求得VeZe=－V0δx0唯一的精确解为

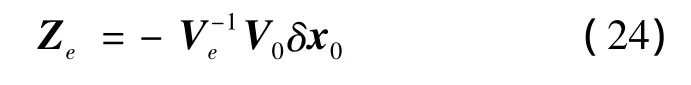
由此可得

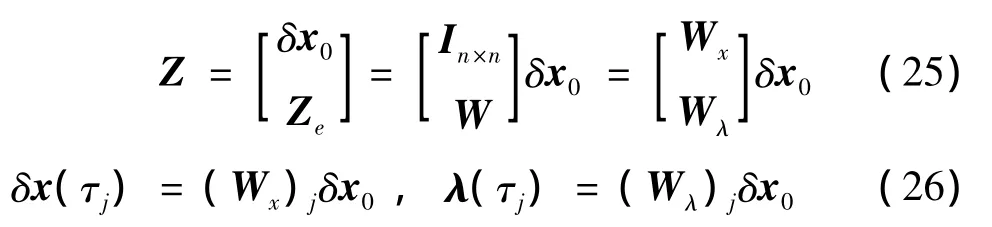
式中:W∈R(2N+2)n×n，Wx、Wλ∈R(N+1)n×n，(Wx)j、(Wλ)j∈Rn×n分别为Wx、Wλ中对应于 τj时刻的子矩阵。

将式(26)代入式(8)，当初始时刻的状态量偏差值δx0已知时，最优反馈控制律在离散节点处的值可以表示为

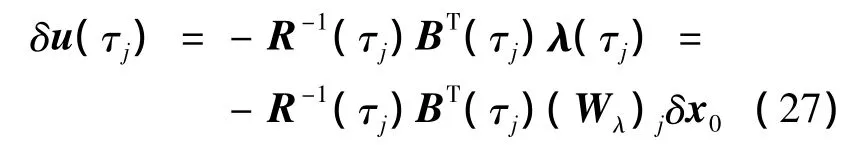
非离散节点处的标称控制量和最优反馈控制律求得的控制量偏差值则根据离散节点处的值通过Lagrange插值的方法获得。

3 闭环制导律

本文研究的滑翔段轨迹跟踪制导律的执行过程如图1所示，对应的流程如下:

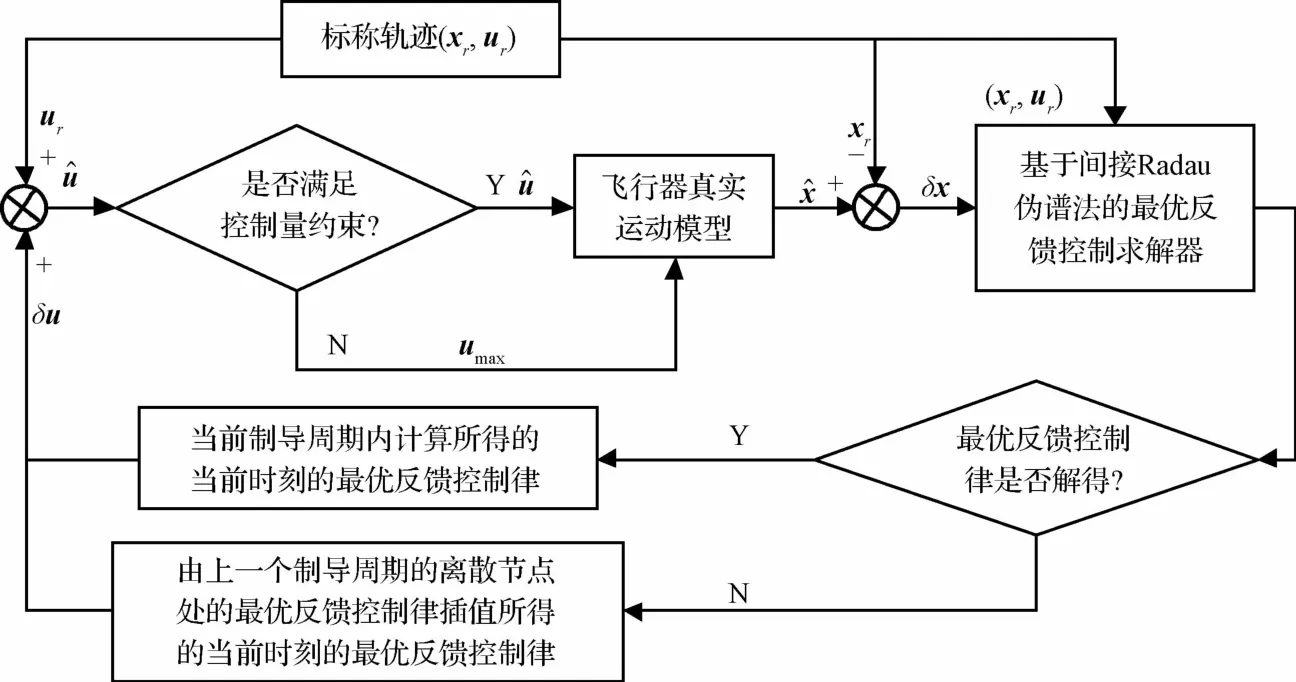
图1 闭环制导律的执行过程示意图Fig．1 Closed-loop guidance law execution diagram

(2)以当前时刻标称控制量ur与当前制导周期内计算所得的当前时刻最优反馈控制律δu(τ0)之和ur+δu(τ0)作为实际飞行的控制量，转入步骤(4);

(3)以当前时刻标称控制量ur与由上一个制导周期的离散节点处的最优反馈控制律(τj)插值所得的当前时刻最优反馈控制律δu(τ)之和ur+δu(τ)作为实际飞行的控制量，转入步骤(4);

上述滑翔段标称轨迹跟踪制导律不需要离线设计误差反馈增益系数和在线增益调参，在制导指令解算过程中不涉及迭代、在线积分求解Riccati矩阵微分方程等复杂数值运算，计算量小，因此便于在线执行。

4 仿真校验

4．1标称轨迹

以CAV-H飞行器［12］为研究对象，质量m为907 kg，参考面积S为0．48387 m2;飞行任务的端点约束如表1所示，过程约束(包括热流密度Q˙、总过载nz和动压q)和控制量约束如表2所示，标称飞行攻角剖面αref为

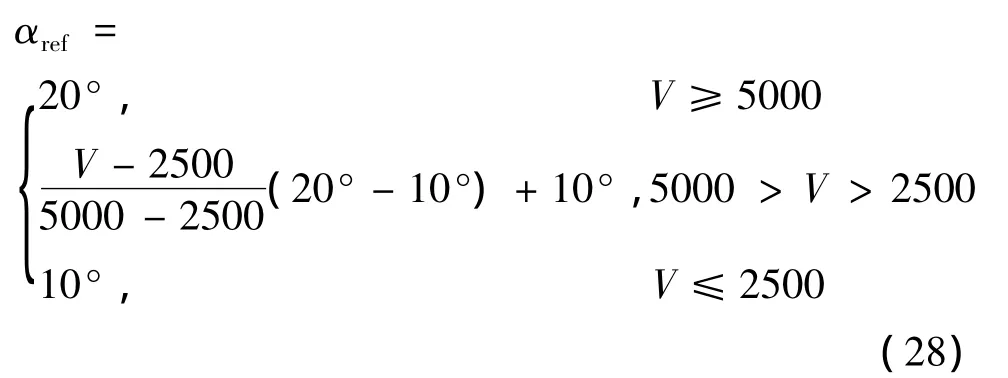
表1 飞行任务的端点约束Table 1 Endpoint constraints for flight mission

表2 过程约束和控制量约束Table 2 Path constraints and control constraints

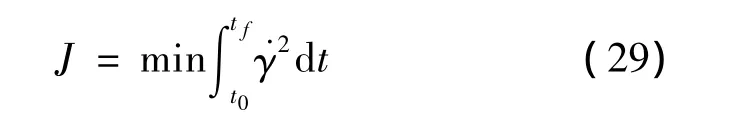
轨迹优化时选择的LGR点数目为40，优化所得轨迹的终端状态量分别为hf=30000 m、θf=65°、φf=3°、Vf=2500 m/s、γf=－0．8536°、ψf=51．6679°，飞行时间为1481．80 s。状态量、控制量和过程约束随飞行时间的变化过程分别如图2～图4中的实线所示。可以看出优化所得的飞行轨迹满足飞行任务的要求且未违背过程约束，这说明优化所得的轨迹是正确和可行的。下文的制导仿真都以本节优化生成的轨迹作为标称轨迹，

4．2制导律鲁棒性验证

为了验证本文的滑翔段制导律的鲁棒性，在飞行器初始状态量存在偏差和质量、气动参数、大气密

利用Radau伪谱法［13］离线优化获得滑翔段的标称轨迹。为满足飞行轨迹平滑的需求，离线轨迹优化采用的性能指标为度等飞行环境参数有扰动情况下进行制导仿真。

仿真环境为双核3．00 GHz主频CPU、3 GB内存及Matlab2012a软件。制导律解算采用的LGR点数目为10，制导周期和积分步长均取为1 s，权值矩阵Sf、Q、R的取值参考Bryson法则［14］，且在本文所有的仿真中，制导周期、积分步长和权值矩阵的取值都一致。制导律仿真过程中，倾侧角σ是主要的轨迹控制量，攻角α只在标称剖面附近进行小范围调整，调整范围如表2中Δα所示。

初始状态量偏差值、飞行环境参数扰动量和闭环制导仿真所得的终端状态量相对于标称轨迹的偏差值如表3所示。其中，组合1和组合2分别对应于 δh0=3000 m、δθ0=0．3°、δφ0=0．3°、δV0=100 m/s、δγ0=0．5°、δψ0=1°和 δh0=－3000 m、δθ0=－0．3°、δφ0=－0．3°、δV0=－100 m/s、δγ0=－0．5°、δψ0=－1°的工况;组合3和组合4分别对应于m(1－5%)、ρ(1－15%)、CL(1－10%)、CD(1－10%)和m(1+5%)、ρ(1+15%)、CL(1+10%)、CD(1+10%)的工况。组合工况下仿真所得的实际状态量、控制量和过程约束随飞行时间的变化过程分别如图2～图4所示。可以看出，在闭环制导律的作用下，实际飞行轨迹未违背过程约束，终端状态量的偏差值满足制导精度的要求。这说明本文的制导律对初始状态量的较大范围偏差和飞行环境参数的有限扰动有良好的鲁棒性。

从表3可以看出，飞行环境参数扰动对制导精度的影响比初始状态量偏差的影响大，制导律在飞行器升阻比存在常值偏差情况下的鲁棒性有限。这是因为在只存在初始状态量偏差情况下，制导律解算用的系统模型很准确;而在飞行环境参数存在扰动时，制导律解算所使用的系统模型中的飞行环境参数与真实的飞行环境参数不一致，制导律解算用的系统模型不准确，从而影响制导律的鲁棒性和制导精度。同时由于控制量数目的限制和过程约束对控制量调节能力(主要是攻角调节能力)的限制，当飞行环境参数存在扰动时，跟踪指定的标称剖面的制导律比跟踪全状态标称轨迹的制导律的鲁棒性更强［7］。

4．3制导律实时性验证

为了验证本文的滑翔段制导律的实时性，选择初始状态量偏差值为δV0=100 m/s的工况，LGR点分别选10、20、30、40和50，对LGR点数目不同的五种工况的仿真结果和制导律解算时间进行对比。从表4可以看出，五种工况的结果都满足制导精度要求;假定在其它计算误差相同的情况下，当LGR点的数目增加到一定量级时，终端状态量偏差值不会再有特别显著的变化;五种工况下制导律平均解算时间和最大解算时间均小于1 s的制导周期，充分说明制导律满足实时性要求。随着LGR点数目增加，制导律平均解算时间也增加，这是因为制导律解算中主要耗时的计算是式(24)中矩阵Ve的求逆，在满足制导精度要求的前提下，选取少量数目的LGR点能够减少矩阵Ve的维数，从而减少制导律解算的耗时。

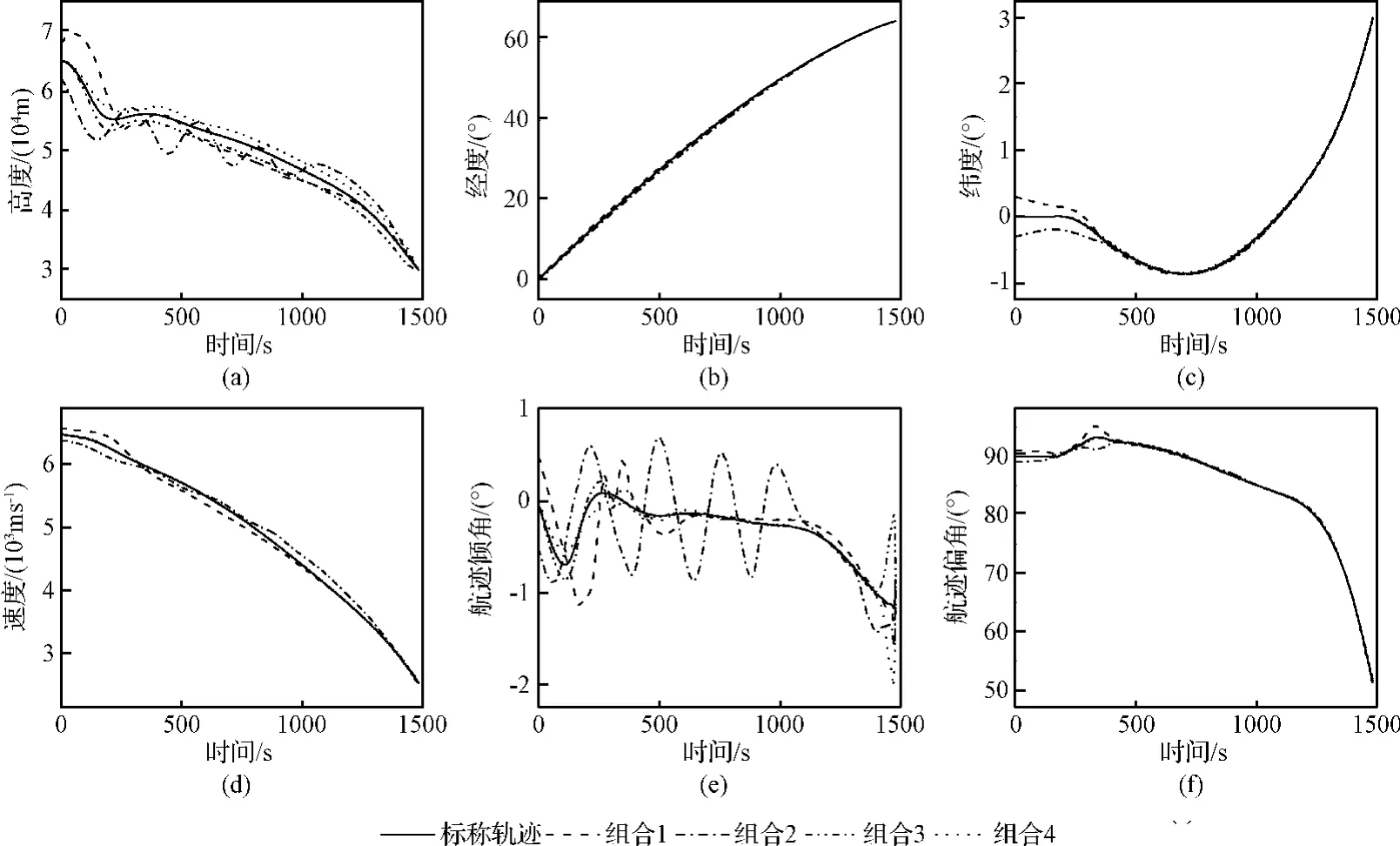
图2 状态量随飞行时间的变化过程Fig．2 Time histories of state variable

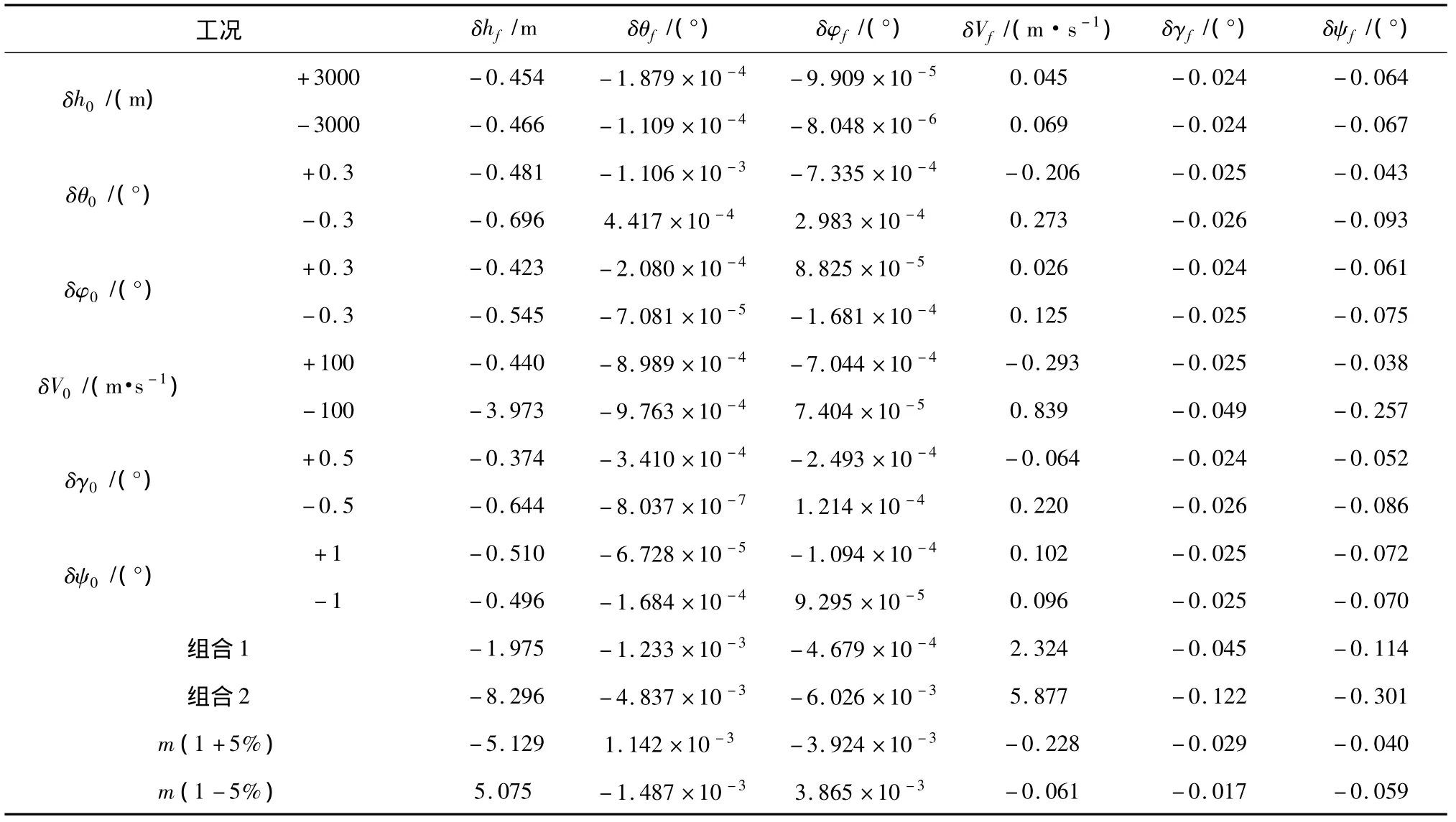
表3 初始状态量存在偏差和飞行环境参数有扰动情况下的终端状态量偏差Table 3 Terminal states deviations of biased initial states and disturbed flight environment parameters conditions

续表

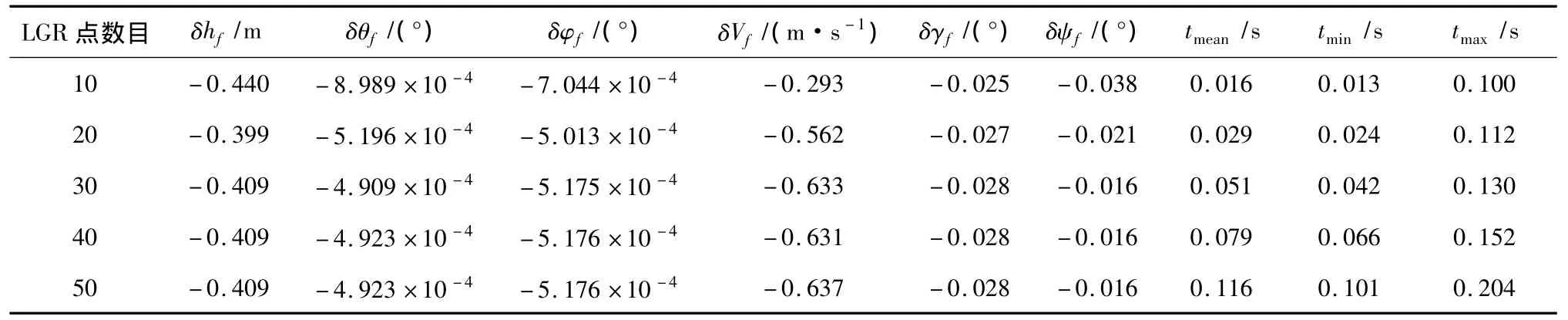
表4 LGR点数目不同时的终端状态量偏差和制导律解算时间Table 4 Terminal states deviations and calculation time of guidance law for different numbers of LGR points

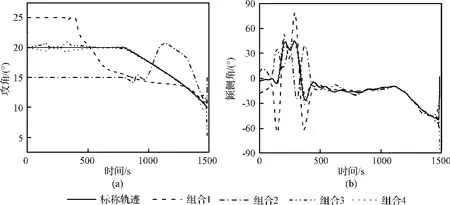
图3 控制量随飞行时间的变化过程Fig．3 Time history of control variable

图4 过程约束随飞行时间的变化过程Fig．4 Time histories of path constraints

5 结论

本文提出了一种新的最优反馈控制求解方法——间接Radau伪谱法，并基于此方法提出了一种高超声速飞行器滑翔段标称轨迹跟踪制导律。制导律解算不存在迭代、在线积分求解Riccati矩阵微分方程等复杂的数值计算，也不包含在线增益调参的过程，便于在线执行;对于不同情况，轨迹跟踪控制器的结构和参数不需要改变。数值仿真结果表明，制导律能满足实时性的要求，在初始状态量存在较大范围偏差和飞行环境参数存在有限扰动的情况下具有良好的鲁棒性;在保证制导精度的前提下，通过选择合适的离散点数目，能够减少制导律的解算时间。

［1］ 胡正东，郭才发，蔡洪．天基对地打击动能武器再入解析预测制导技术［J］．宇航学报，2009，30(3):1039－1044．［Hu Zheng-dong，Guo Cai-fa，Cai Hong．Analytical predictive guidance for space-to-ground kinetic weapon in reentry［J］．Journal of Astronautics，2009，30(3):1039－1044．］

［2］ 水尊师，周军，葛致磊．基于高斯伪谱方法的再入飞行器预测校正制导方法研究［J］．宇航学报，2011，32(6):1249－1255．［Shui Zun-shi，Zhou Jun，Ge Zhi-lei．On-line predictorcorrector reentry guidance law based on Gauss pseudospectral method［J］．Journal of Astronautics，2011，32(6):1249－1255．］

［3］Xue S B，Lu P．Constrained predictor-corrector entry guidance［J］．Journal of Guidance，Control，and Dynamics，2010，33(4):1273－1281．

［4］ 陈刚，康兴无，闫桂荣，等．基于伪谱方法的自适应鲁棒实时再入制导律研究［J］．系统仿真学报，2008，20(20):5623－5634．［Chen Gang，Kang Xing-wu，Yan Gui-rong，et al．Real time robust adaptive reentry guidance law based on pseudospectral method［J］．Journal of System Simulation，2008，20(20):5623－5634］．

［5］Roenneke A J，Cornwell P J．Trajectory control for a low-lift re-entry vehicle［J］．Journal of Guidance，Control，and Dynamics，1993，16(5):927－933．

［6］ 南英．航天飞机再入抗干扰轨道优化设计［D］．西安:西北工业 大 学，1990．［Nan Ying．Anti-disturbance reentry trajectory optimization design for the Space Shuttle［D］．Xi’an:Northwestern Polytechnical University，1990．］

［7］Lu P．Regulation about time-varying trajectories:precision entry guidance illustrated［J］．Journal of Guidance，Control，and Dynamics，1999，22(6):784－790．

［8］Tian B L，Zong Q．Optimal guidance for reentry vehicles based on indirect legendre pseudospectral method［J］．Acta Astronautica，2011，68(7):1176－1184．

［9］Zhou H，Tawfiqur R，Wang D W，et al．Onboard pseudospectral guidance for re-entry vehicle［J］．Proceedings of the Institution of Mechanical Engineers，Part G:Journal of Aerospace Engineering，2014，228(11):1925－1936．

［10］ 吴旭忠，唐胜景，郭杰，等．基于滚动时域控制的再入轨迹跟踪制导律［J］．系统工程与电子技术，2014，36(8):1602－1608．［Wu Xu-zhong，Tang Sheng-jing，Guo Jie，et al．Trajectory tracking guidance law for reentry based on receding horizon control［J］．Systems Engineering and Electronics，2014，36(8):1602－1608．］

［11］Yan H，Fahroo F，Ross I M．Optimal feedback control laws by legendre pseudospectral approximations［C］．The American Control Conference，Arlington，USA，June 25－27，2001．

［12］Phillips T H．A common aero vehicle(CAV)model description and employment guide［R］．Schafer Corporation for AFRL and AFSPC，2003．

［13］Garg D，Patterson M A，Darby C L，et al．Direct trajectory optimization and costate estimation of finite-horizon and infinitehorizon optimal control problems using a Radau Pseudospectral Method［J］．Computational Optimization and Applications，2011，49(2):335－358．

［14］Bryson A E，Ho Y C．Applied optimal control:optimization，estimation and control［M］．Washington DC:Hemisphere Publishing Company，1975．