高延性纤维混凝土抗压韧性试验研究
邓明科,刘海勃,秦 萌,2,梁兴文
(1.西安建筑科技大学土木工程学院,陕西 西安 710055;2.成都天华西南建筑设计有限公司,四川 成都 610016)
高延性水泥基复合材料[1](Engineered Cementitious Composites,简称ECC)是20世纪90年代美国Michigan大学Victor C. Li教授首先提出的一种具有高韧性、高抗裂性能和耐损伤能力的新型结构材料.ECC在拉伸和剪切荷载下表现出良好的多裂缝开展和应变硬化特征,可显著提高混凝土材料的韧性和耐损伤能力,在土木工程领域具有广泛的应用前景.Li等通过对纤维、基体和界面特性进行研究,提出了ECC的微观力学模型[2];公成旭等研究了PVA纤维直径对ECC抗拉性能的影响[3];张君等研究了基材强度(水胶比)对ECC抗弯性能的影响[4];庞超明等研究了粉煤灰掺量、胶砂比等对高延性水泥基复合材料力学性能的影响[5];李贺东等研究了超高韧性水泥基复合材料(UHTCC)的受弯性能及弯曲韧性评价方法[6].为便于ECC在混凝土结构中的推广应用,本课题组将其称为高延性纤维混凝土(High Ductile Fiber Reinforced Concrete,简称HDC),并系统开展了高延性纤维混凝土抗压性能、抗弯性能和尺寸效应的试验研究[7-8].
轴心抗压性能是混凝土材料的基本力学性能指标之一.普通混凝土受压破坏呈明显脆性,高延性纤维混凝土表现出良好的韧性和耐损伤能力,其抗压韧性也成为其重要的力学性能指标.韧性反映了材料吸收能量和抵抗断裂破坏的能力.当基体开裂后,纤维从基体中拔出时需要克服界面摩擦力而消耗较大的能量,使高延性纤维混凝土开裂以后仍具有良好的完整性.蔡向荣等进行了UHTCC单轴受压韧性的试验测定与评价[9];徐世烺等通过单轴受压试验,得到UHTCC的塑性变形能力和峰值后延性明显优于混凝土[10].
为进一步研究高延性纤维混凝土的抗压韧性和变形能力,本文选取100 mm×100 mm×300 mm的棱柱体试块,进行了9组不同配合比HDC的单轴受压试验,分别考虑纤维掺量、水胶比、粉煤灰掺量和砂胶比对其抗压韧性的影响,确定HDC的抗压韧性的评定方法,为高延性纤维混凝土的工程应用提供依据.
1 试验概况
1.1 试件设计和试验方法
试验采用的高延性纤维混凝土基本组成为:水泥(P·O 42.5R)、粉煤灰、精细河砂、PVA纤维、水和高效减水剂.PVA纤维的具体参数见表1,试验配合比设计见表2,其中配合比1为不含纤维的水泥砂浆基体对比试件.

表1 PVA纤维各项性能指标Tab.1 Properties of PVA fiber

表2 试验配合比Tab.2 Mix of test
每组试件包括3个尺寸为100 mm×100 mm×300 mm的棱柱体,试件均在同条件下制作、养护.试验时试件的龄期为10个月,采用500 t电液伺服压力试验机进行加载,加载速率为0.5 mm/min.试验加载装置如图1所示.

图1 试验加载装置Fig.1 Test loading device
1.2 试验现象
砂浆基体的受压破坏过程与普通混凝土类似,试件出现竖向裂缝以后,立即丧失承载力,发生明显的脆性破坏.
高延性纤维混凝土试件的受压破坏过程与砂浆基体差别较大.加载过程中,高延性纤维混凝土试件经历了无裂缝阶段、裂缝稳定发展、裂缝非稳定发展等过程,具体描述如下:
加载初期,试件横向变形较小,应力-应变曲线呈线性关系,试件处于弹性阶段;加载至峰值荷载的50%~60%时,试件横向变形增大,表面开始出现竖向微裂缝,纤维桥联作用使基体内部裂缝扩展受到一定约束,应力-应变曲线基本呈线性关系,试件基本还处于弹性阶段;当加载至峰值荷载的80%以上时,试件表面裂缝逐渐变宽,此时应变增长的速度大于应力增长的速度,应力-应变曲线发生弯曲,试件单轴受压的塑性变形逐渐增大,试件横向拉伸变形较大时形成一条主裂缝,试验过程中可听到主裂缝变宽时纤维拔出或拉断的“嘶嘶”声.试件达到峰值荷载以后,主裂缝突然变宽,承载力降低,试件变形继续增大.当荷载下降峰值荷载的10%~20%以后,主裂缝两侧试件发生明显错动,试件承载力下降缓慢.试件破坏以后始终保持一定的剩余承载力.各试件受压破坏后的裂缝形态如图2所示.

图2 试件破坏形态Fig.2 Failure mode of test specimens
2 试验结果及分析
2.1 单轴受压荷载-变形曲线
试验测得各组试件单轴受压的荷载-变形曲线如图3所示.表3给出了各组试件的峰值荷载和变形.
由图3和表3可以看出,砂浆基体(配合比1)对应峰值应变为0.002 2,与《混凝土结构设计规范》[11]相应混凝土的峰值应变接近.高延性纤维混凝土单轴受压的荷载-变形曲线为单峰曲线,其峰值变形较砂浆基体试件均有明显提高,9组不同配合比HDC的峰值变形可达砂浆基体的2.31~3.64倍,表明HDC达到峰值荷载以前的变形能力得到明显提高.另外,HDC试件受压破坏以后具有良好完整性,当试件产生较大的压缩变形时仍具有10%~20%的剩余承载力.

表3 试验结果Tab.3 Test results
2.2 韧性指数分析
我国《纤维混凝土试验方法标准》[12]关于等效弯曲强度ef的计算方法如下:

式中:ef为等效弯曲强度,MPa;kΩ为跨中挠度为/150L的荷载-挠度曲线下的面积,N mm⋅;kδ为跨中挠度为 /150L 时的挠度值.
本文参照等效弯曲强度的计算方法,根据HDC试件单轴受压的荷载-变形曲线,提出等效抗压强度(图4)的计算公式如下:
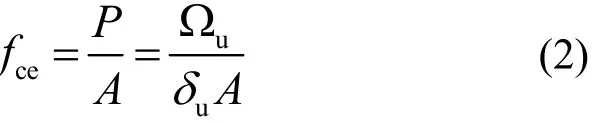
式中:P为轴向压力, N; fce为等效抗压强度, MPa;Ωu为竖向变形量为δu时荷载-变形曲线下的面积,N·mm;δu为荷载下降至极限荷载的u倍(可取0.85、0.50或0.20)所对应的竖向变形量, mm;A为试件单轴受压的面积.
抗压韧性反映了材料受压破坏过程中吸收能量和抵抗破坏的能力,与材料抗压强度和变形能力有关.按式(2)计算的等效抗压强度,反应了试件破坏过程中承载力下降至某一定值时对应的平均抗压强度,但未考虑试件破坏过程中压缩变形的影响,不能有效反映试件的抗压韧性.
为考虑试件变形对抗压韧性的影响,对式(2)采用无量纲比值δu/l(l为试件高度)进行修正如下:
定义cuW 为等效抗压韧性指数,由式(3)可知,其物理意义为试件单轴受压时单位体积的变形能,可作为试件的抗压韧性评价指标.
下面以a、b两个试件的单轴受压荷载-变形曲线(图5)为例进一步说明等效抗压韧性指数的物理意义.当u取0.85时,图4中为的1.60倍,说明试件b的抗压韧性明显高于试件a,按式(2)计算可得/=1 .06,按式(3)计算可得/=1 .66.可 见,等效抗压韧性指数 Wcu综合了反映试件的抗压强度和变形能力两个因素的影响,可有效反映试件单轴受压的抗压韧性.
根据以上试验结果,当u取0.85、0.50和0.20时,试件等效抗压韧性指数的计算结果见表4.

图4 等效抗压强度计算Fig.4 The calculation of equivalent compressive strength

图5 不同曲线对比分析Fig.5 Comparative analysis of the different curves

表4 等效抗压韧性指数计算结果Tab.4 Calculation results of equivalent compressive toughness
2.3 各因素对韧性指标的影响分析
根据表4的计算结果,本试验中纤维掺量、水胶比、粉煤灰掺量和砂胶比四种因素对HDC抗压韧性的影响趋势如图6.
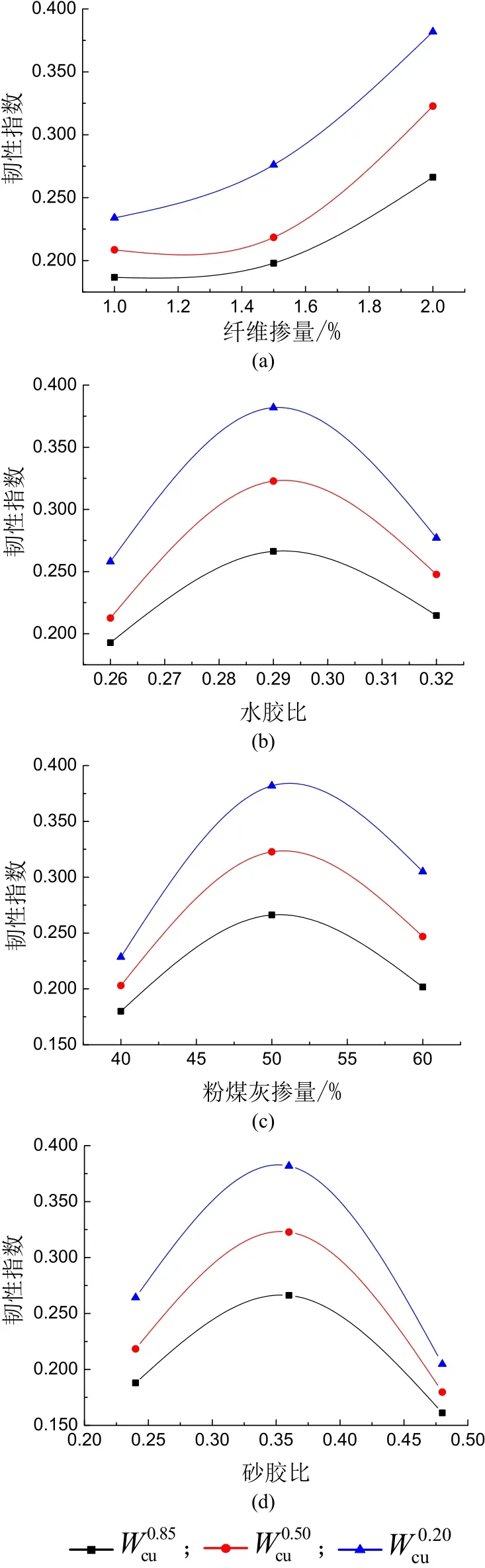
图6 各因素对抗压韧性指标的影响趋势Fig.6 The trend of Various factors for the Compressive toughness
各因素的影响分析如下:
(1) 纤维掺量
砂浆基体试件为典型的脆性材料,抗压韧性很小,其压缩变形和等效抗压韧性指数明显低于其余试件.高延性纤维混凝土基体内部乱向分布的短纤维能有效阻止内部微裂缝的产生和发展,提高了试件单轴受压的变形能力和抗压韧性.由图6(a)可见,随着纤维掺量增大,试件的等效抗压韧性指数明显提高.当纤维掺量由1%增加到2%时,、、分别提高了42.66%、54.78%和63.28%.
(2) 水胶比
随着水胶比减小,基体的抗压强度提高;但水胶比较低时,拌合物的和易性较差,基体内部纤维分散不均匀,使得纤维的增韧作用减弱.由图6(b)可以看出,本次试验中水胶比为0.29的试件单轴受压变形能力和抗压韧性指数达到最大值.
(3) 粉煤灰掺量
粉煤灰可以改善纤维与基体之间的界面特性,在一定程度上提高材料的延性.随着粉煤灰掺量增大,基体的抗压强度降低,但抗压韧性有所提高.从图6(c)中可以得出:当掺量小于50%时,其抗压韧性指数随粉煤灰掺量增加而增大;当掺量超过50%,由于试件龄期的影响,其抗压强度未得到充分发挥,导致抗压韧性指数降低.
(4) 砂胶比
砂胶比增大,高延性纤维混凝土的抗压强度有所提高,但在一定程度上抑制了材料的应变硬化特性,导致其抗压韧性降低.由图6(d)可以看出:当砂胶比由0.36增加至0.48时,其抗压韧性指数、、分别降低了39.5%,44.3%,46.3%.
2.4 抗压韧性指数与纤维掺量之间的关系
高延性纤维混凝土的受压破坏明显区别于砂浆基体,主要取决于基体内部乱向分布的PVA纤维,纤维的桥联作用使试件纵向压缩时受到一定的横向约束作用,改善了HDC的受力状态和开裂以后的变形能力,从而提高了材料的抗压韧性.
由表3和表4可得,改变纤维掺量时,纤维桥联作用对HDC单轴抗压强度的提高作用不明显,但对抗压韧性指数 Wc0u.85的提高可达砂浆基体的2.88~4.09倍,对受压变形能力的提高可达砂浆基体的3.41~3.64倍.因此,纤维掺量是影响试件抗压韧性指数的主要因素.为进一步分析纤维掺量与试件抗压韧性指数之间的定量关系,对表4中改变纤维掺量的试件抗压韧性指数进行线性回归分析,得到等效抗压韧性指数与纤维掺量φ之间的关系如图7所示,其表达式为:
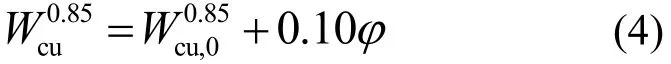

图7 与φ的关系Fig.7 Relationship between equivalent compressive toughness index and volume ratio of PVA fiber
2.5 试件受压变形能力分析
高延性纤维混凝土基体内部的纤维桥联作用,使试件纵向受压产生的竖向裂缝和横向拉伸变形受到均匀连续的约束力.因此,HDC单轴受压的受力状态相当于处于常规三轴受压的约束混凝土.
本文的试验结果表明,纤维桥联作用对HDC单轴抗压强度的提高作用不明显,但对抗压韧性指数的提高可达砂浆基体的2.88~4.09倍,对受压变形能力的提高可达砂浆基体的3.11~3.64倍.
为了定量描述纤维桥联作用对试件受压变形能力的提高,以下将HDC中纤维桥联作用对基体的产生的横向约束与箍筋约束作用进行等效分析.采用Mander等[13]提出的约束混凝土模型,对HDC中纤维桥联作用产生的横向约束作用进行等效分析,具体过程如下:
箍筋约束混凝土的受压峰值应变
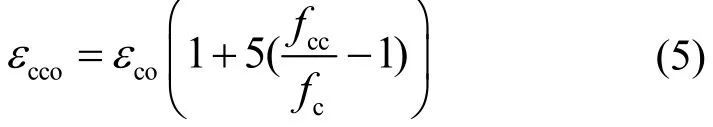
式中,coε为混凝土(基体)的峰值应变.ccf可按式(6)计算
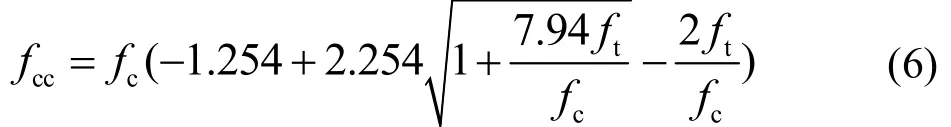
式中:tf为箍筋对混凝土(基体)提供的侧向约束应力;cf为混凝土(基体)的抗压强度.
混凝土的纵向受压破坏是由于其横向拉裂引起,高延性纤维混凝土试件受压破坏过程中,基体内部的纤维桥联作用,使试件纵向受压产生的竖向裂缝和横向拉伸变形受到约束.HDC的拉伸应变硬化效应,使试件横向拉裂以后还能继续受到持续稳定的横向约束力,其受力机理如图8.

图8 横向约束力Fig.8 Lateral binding force
假定HDC单轴受压时基体受到的横向约束应力(纤维桥联应力σt)不超过其抗拉强度ft.根据试验结果,取 εco= 0 .002 2.参考文献[14]中本课题组已有的试验数据,可得配合比4对应的HDC抗拉强度平均值 ft=5 .7 MPa ,本次试验测得砂浆基体的抗压强度平均值 fc=63.06 MPa .将ft、fc和εco带入公式(5)和(6),可得配合比4对应的HDC单轴受压的峰值应变为 εcco= 0 .007 9.
可见,按纤维桥联应力产生的横向约束力等效分析,求得HDC试块单轴受压的峰值应变可达砂浆基体的3.59倍,与本文配合比4的试验结果基本相符.
以下进一步分析纤维桥联应力tσ与约束混凝土体积配箍率之间的等效换算关系.

图9 纤维桥联应力与箍筋约束力等效Fig.9 The equivalence of fiber bridging force and stirrup binding force

由式(7)得

以截面尺寸为500 mm × 5 00 mm的钢筋混凝土柱为例,内配箍筋采用HRB400,直径为10 mm,保护层厚度为25 mm.则 b = 450 mm, Asv= 78.5 mm2,n=2,令σt=ft=5.7 MPa,fyv=360 N/mm2,代入式(8)可得s=23 mm.
我国《混凝土结构设计规范》[11]规定矩形截面柱的体积配箍率为

其中,l1= l2=4 50 mm ,Acor=2 02 500 mm2, As1As2=78.5 mm2, n1= n2=2 ,代入式(9)可求得HDC纤维桥联应力对应的等效体积配箍率为ρv= 3.03%,远远高于框架柱端加密区对体积配箍率的要求.
以上分析表明,HDC良好的拉伸应变硬化效应和基体内部的纤维桥联约束作用,可阻止基体内部微裂缝的产生与发展,相当于在试件内配置了大量约束箍筋,使试件单轴受压的变形能力明显提高,表现出良好的抗压韧性.因此,将HDC用于结构关键部位及构件塑性铰区,不仅可以显著提高塑性铰区的变形能力,还可减少约束箍筋的数量.
3 结论
本文通过对9组不同配比的高延性纤维混凝土试件的单轴受压试验研究,初步得出以下结论:
(1) 高延性纤维混凝土单轴受压的峰值应变较砂浆基体有明显提高,可达砂浆基体的2.31~3.59倍,且试件产生较大的压缩变形时仍具有10%~20%的剩余承载力.
(2) 采用等效抗压韧性指数cuW 反映了试件单轴受压时单位体积的变形能,可作为试件的抗压韧性评价指标;随着纤维掺量增大,HDC试件的等效抗压韧性指数明显提高.
(3) HDC纤维桥联作用对单轴抗压强度的提高作用不明显,但对等效抗压韧性指数和受压变形能力的提高可达砂浆基体的3倍以上.
(4) 纤维掺量是影响HDC抗压韧性指数的主要因素,根据试验结果建立了HDC等效抗压韧性指数与纤维掺量φ之间的关系.
(5) 通过HDC纤维桥联应力与箍筋约束作用等效分析表明,HDC基体内部的纤维桥联作用,相当于在试件内配置了大量约束箍筋,使试件的抗压韧性和受压变形能力明显提高.
References
[1] LI V C, LEUNG C K Y. Steady state and multiple cracking of short random fiber composites[J]. ASCE Journal of Engineering Mechanics, 1992, 118(11): 2246-2264.
[2] LI V C, MIHASHI H, WU H C, et al. Micromechanical Models of Mechanical Response of HPFRCC [C]// High Performance Fiber Reinforced Cementitious Composites,Rilem Proceedings 31, Eds. A. E. Naaman and H. W.Reinhardt, 1996: 43-100.
[3] 公成旭, 张君. 水灰比及粉煤灰掺量对高韧性纤维增强水泥基复合材料单轴抗拉性能的影响[J]. 水利学报,2008, 139(3): 361-366.GONG Chengxu, ZHANG Jun. Uniaxial tension behavior of high ductile fiber reinforced cementitious composite with focus on some influencing factors[J]. Journal of Hydraulic Engineering, 2008, 139(3): 361-366.
[4] 张君, 公成旭, 居贤春, 等. 延性纤维增强水泥基复合材料的抗弯性能[J]. 工程力学, 2010(3): 112-115.ZHANG Jun, GONG Chengxu, JU Xianchun, et al.Bending Performance Of Ductile Fiber Reinforced cementitious composite[J]. Engineering Mechanics,2010(3): 112-115.
[5] 庞超明, LEUNG C K Y, 孙伟. 高掺量粉煤灰高延性水泥基复合材料的制备和性能[J]. 硅酸盐学报, 2009(12):2071-2077.PANG Chaoming, LEUNG C K Y, SUN Wei. Preparation and properties of high ductility cementitious composites with high content of fly-ash[J]. Journal of the Chinese Ceramic Society, 2009(12): 2071-2077.
[6] 李贺东, 徐世烺. 超高韧性水泥基复合材料弯曲性能及韧性评价方法[J]. 土木工程学报, 2010(3): 32-39.LI Hedong, XU Shilang. High toughness cementitious composites bending properties and toughness evaluation method[J]. China Civil Engineering Journal, 2010(3):32-39.
[7] 邓明科, 常云涛, 梁兴文, 等. 高延性水泥基复合材料抗压强度尺寸效应的正交试验研究[J]. 工业建筑,2013(7): 80-85.DENG Mingke, CHANG Yuntao, LIANG Xingwen, et al. Orthogonal test research on compressive strength size effect of engineered Cementitious Composites[J]. Industrial Construction, 2013(7): 80-85.
[8] 邓明科, 孙宏哲, 梁兴文, 等. 延性纤维混凝土抗弯性能的试验研究[J]. 工业建筑, 2014(5): 85-90.DENG Mingke, SUN Hongzhe, LIANG Xingwen, et al.Experimental study of flexural behavior of ductile fiber reinforced concrete[J]. Industrial Construction, 2014, 05:85-90.
[9] 蔡向荣, 徐世烺. UHTCC单轴受压韧性的试验测定与评价指标[J]. 工程力学, 2010, 27(5): 218-239.CAI Xiangrong, XU Shilang. Experimental measurement and evaluation indexes of toughness properties for UHTCC under uniaxial compression[J]. Engineering Mechanics, 2010, 27(5): 218-239.
[10] 徐世烺, 蔡向荣, 张英华. 超高韧性纤维增强水泥基复合材料单轴受压应力-应变全曲线试验测定与分析[J].土木工程学报, 2009, 42(11): 79-85.XU Shilang, CAI Xiangrong, ZHANG Yinghua. Experimental measurement and analysis of the axial compressive stress-strain curve of Ultra High Toughness Cementitious Composites[J]. China Civil Engineering Journal, 2009, 42(11): 79-85.
[11] GB 50010-2010 混凝土结构设计规范[S]. 北京: 中国建筑工业出版社, 2011.GB 50010-2010 Code for design of concrete structures[S]. Beijing: China Architecture & Building Press,2011.
[12] CECS13: 2009 纤维混凝土试验方法标准[S]. 北京:中国计划出版社, 2010.CECS13: 2009 Standard test methods for fiber reinforced concrete[S]. Beijing: China Planning Press, 2010.
[13] MANDER J B, PRIESTLEY M J N, PARK R. Theoretical stress-strain model for confined concrete[J]. Journal of structural engineering, 1988, 114(8): 1804-1826.
[14] 邓明科, 卢化松, 杨开屏, 等. 型钢高延性混凝土短梁抗剪性能试验研究[J]. 建筑结构学报, 2015, 36(10):65-72.DENG Mingke, LU Huasong, YANG Kaiping, et al. Experimental study of shear behavior of steel high ductile concrete beams[J]. Journal of Building Structures, 2015,36(10): 65-72.

