基于神经网络的石墨烯弹性参量识别方法研究

华 军，武霞霞，李东波，张宇辉

(西安建筑科技大学理学院，陕西 西安 710055)

石墨烯(graphene)，又称为二维石墨片，是由单层碳原子通过共价键结合而成的具有规则六方对称的理想二维晶体[1-2]，是2004年由英国曼彻斯特大学的安德烈·盖姆(Andre Geim)和康斯坦丁·诺沃肖罗夫(Konstantin Novoselov)首先发现的，是继富勒烯(C60)和碳纳米管(CNTs)之后的又一种新型低维材料，其厚度仅为头发丝直径的20万分之一，约为0.335 nm，是目前发现的最薄的层状材料，具有超高的强度、刚度和韧性，被誉为是具有战略意义的新材料.

准确把握石墨烯基本弹性参量是了解石墨烯力学性能的重要指标.自从石墨烯问世以来，国内外学者针对其弹性参量进行了大量的研究工作.现研究方法主要有实验方法、分子动力学方法、量子力学方法等，但实验方法测定石墨烯弹性参量的成本较高，试验结果受到试验条件、操作熟练程度等的影响.分子动力学和量子力学等数值模拟方法受计算规模的限制，计算量大且计算尺度有限[3-4].因此，寻求快速、便捷的方法对石墨烯弹性参量进行预测具有重要意义.

石墨烯的力学性能的影响因素较多，各个因素之间形成为一个复杂的非线性关系，普通数学模型很难准确表达弹性参量与各因素之间的关系[5].经网络具有很强的非线性、自组织、自学习能力，能够很好地处理非线性信息，已应用于许多领域.Venkatesh[6]等人通过人工神经网络预测方法对氢功能化石墨烯的机械性能进行了研究，发现该种计算技术可以作为一个强大的工具来预测功能化氢石墨烯的抗拉强度.尹海莲[7]等人以碳/陶瓷复合材料性能与成分的关系为研究对象，利用BP 算法建立了复合材料性能预测模型.和试验值相比较表明, 所建立的网络能反映复合材料组分与其材料性能之间的关系，为实验设计提供了新的思路.白光辉[8]等人采用人工神经网络(ANN)对炭/炭复合材料烧蚀性能进行了预测.采用人工神经网络对炭/炭复合材料的烧蚀性能进行预测时误差小于11 %，满足工程实践的精度要求.关于石墨烯基础性能的研究是纳米材料的研究热点之一，但是对石墨烯弹性参量的预测还鲜有报道.因此，利用神经网络对石墨烯的弹性参量进行预测，旨在寻求一种快速、简捷的石墨烯弹性参量计算方法.

1 石墨烯弹性参量的BP预测模型

从现有文献中，搜集数据作为学习样本，建立人工神经网络的BP模型，通过网络的自组织、自学习获得足够的信息后，输入影响石墨烯弹性参量的参数，可获得石墨烯弹性参量的数值.模型的输入是石墨烯弹性参量的各影响因素，输出值是弹性模量和剪切模量.

1.1 预测模型的构建

1.1.1 输入层和输出层参数的确定

构建BP预测模型，其输入层的神经元节点数由影响石墨烯弹性参量的因素而定，根据以往的研究，主要考虑到的影响因素有：长度、宽度、长宽比、手性(扶手型和锯齿型)、层数及温度.输出层节点为石墨烯的弹性模量与剪切模量.因此，预测模型中的输入层 6=n ，输出层 2=m .

1.1.2 隐含层参数的确定

根据 Kolmogorov定理指出，给定任一个连续函数 f : U n→ R n,f ( X )=Y，这里U是闭单位区间[0，1]，f可以精确地用一个三层前向网络实现，此网络的第一层(即输入层)有n个处理单元，中间层有2 n + 1个处理单元，第三层(即输出层)有m个处理单元.因此，构建神经网络模型采用一个隐含层，隐含层选用13个节点[9-10].1.1.3 预测模型

根据所确定的隐含层层数及输入层、隐含层、输出层节点数，构建的预测模型为6-13-2的BP模型，如图1所示.

1.1.4 激发函数

BP神经网络传递函数常用的有 Sigmoid型对数、正切函数和线性函数，本模型采用有一定阈值特性的连续可微的Sigmoid函数之一的非对称性S型函数作为神经元的激发函数，同时网络采用梯度下降法进行学习[10-11].S型函数为

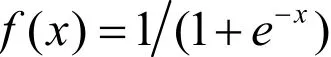
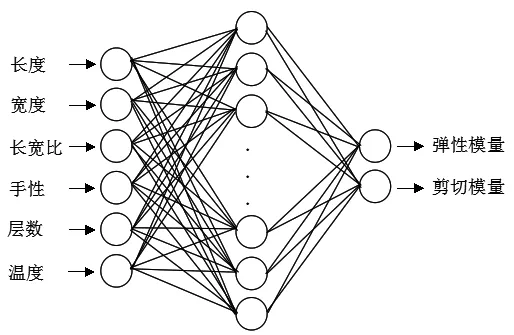
图1 石墨烯等效弹性参量的BP人工神经网络预测模型Fig.1 BP neural network prediction model of graphene equivalent elastic parameter

2 模型的训练及检验

2.1 训练及检验样本的选取

考虑BP神经网络样本的选取应具有代表性、普遍性及均衡性的原则，从现有文献中[12-16]选取了84组数据(为节省篇幅表1列出部分数据)，其中69组作为训练样本，15组为检验样本.

2.2 数据的归一化处理

归一化是使数据在0～1之间概率分布.当所有样本的输入信号都为正值时，与第一隐含层神经元相连的权值只能同时增加或减小，从而导致学习速度很慢，并可能引起网络无法收敛.为了避免出现这种情况，加快网络学习速度，降低网络结构的复杂性以及提高网络的精度，需要对输入信号进行归一化，使样本数据介于到[－1，1]之间[9,11].MATLAB提供的预处理方法有：归一化处理,所涉及的函数有premnmx、postmnmx、tramnmx.对于输入矩阵 p和输出矩阵t进行归一化处理的语句为：[pn, minp,maxp, tn, mint, maxt]=premnmx(p,t)；对目标矩阵p2进行归一化处理的语句为：[pn]=tramnmx(p, minp,maxp)；训练结束后，用postmnmx函数对预测值进行反归一化处理得到最终预测值：an=postmnmx(net, pn).表2为将表1数据归一化后的结果.

2.3 模型的训练及检验

根据 MATLAB神经网络工具箱所提供的函数[12]，利用归一化后的数据对构建的模型进行训练.其中，网络训练时训练函数选取带有动量项的梯度下降法traingdm，增加动量项目的是为了避免网络训练陷于较浅的局部极小点；权值和阈值的BP学习算法为 learngdm；网络的性能函数默认为mse.训练参数的设置如表3所示：

训练样本时间为12小时43分钟，经过2.5×105步学习收敛，精度达到 0.001，误差随训练次数的变化曲线如图2所示.训练结束后，对原样本数据进行预测，生成预测值，并对预测值进行反归一化处理得到最终预测值.

表1 训练及检验样本的部分数据Tab.1 Partial data of training and forecasting sample

表2 归一化后部分网络样本数据Tab.2 Partial data of the network sample after normalization

2.4 预测结果及误差分析

本文构建的预测模型通过网络的自学习，达到了指定的性能指标，神经网络中存储了样本包含的内在非线性映射关系，确定了各输入、输出层间的权值和阈值.

表4给出了预测值与实际值的误差，其中弹性模量E的平均相对误差为2.799 %，最大误差为5 %，最小误差为0.693 %.剪切弹性模量G的平均相对误差为2.222 %，最大误差为6.210 %，最小误差为0.105 %.表明BP神经网络预测在石墨烯等效弹性参量预测方面误差较小，满足预测精度要求.

表3 参数设置表Tab.3 Parameter setting

图2 误差随训练次数变化曲线图Fig.2 Graphene of error varying with training times

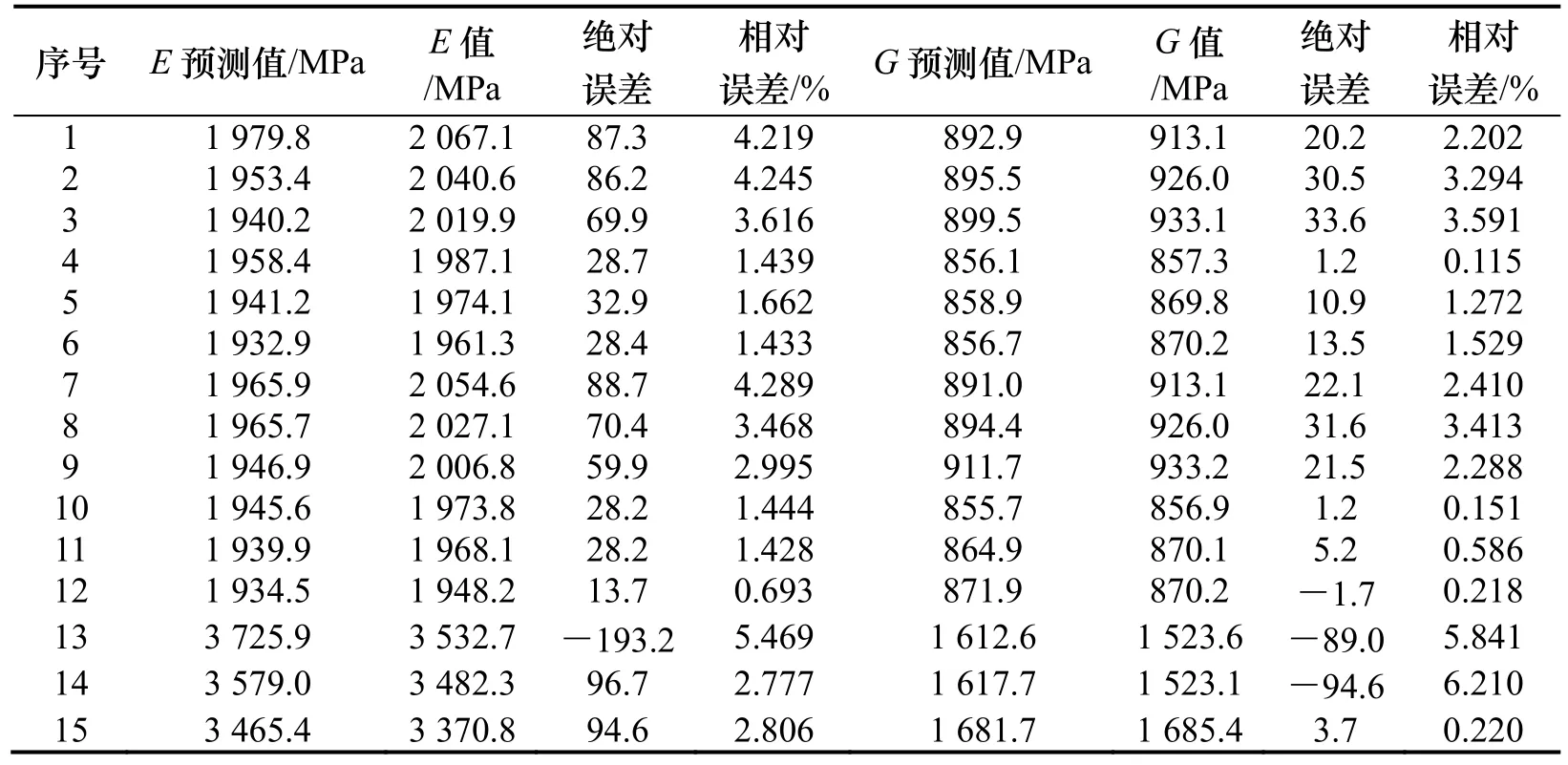
表4 预测结果及误差Tab.4 The prediction results and errors

3 等效弹性参量影响因素敏感性分析

3.1 正交表的选用

正交表，其符号是 Ln(mk)，其中L表示正交表；n表示正交表的横行数 (可安排的试验次数)；k表示正交表的纵列数，即能容纳的试验因素个数；m表示各试验因数的位级(水平)数.因素在试验中所处的状态、条件的变化可能会引起试验指标的变化，将因素变化的各种状态和条件称为因素的位级.根据行业标准《工艺参数优化方法正交实验法(JB/T 7510-1994)》，选用水平正交表，一般要求，因素数小于正交表列数，因素水平数与正交表对应的水平数一致，在满足上述条件的前提下，确定因素位级数为5，因素个数为6个，分别为影响石墨烯弹性参量的 6个影响因素[9]。因素位级见表 5，其中第3位级即为石墨烯弹性参量各影响因素的初始值.最后根据位级数和因素数选定L25(56)正交表.3.2 弹性参量对影响因素的灵敏性分析

通过构建的6-13-2石墨烯弹性参量预测BP模型的训练与检验，验证了该方法的可行性和适用性.因此，可用训练后的网络对同类问题进行预测.样本描述：石墨烯薄膜长度为21.839 nm，宽度为4.898 nm，长宽比为4.459，手性为锯齿型，层数为1，温度为500 K.

分析方法：由以上样本中石墨烯影响因素的具体数值，通过因素位级表计算得出样本位级变化表，然后将L25(56)正交表中位级数对应的各个因素值组合形成25个试验学习样本.用训练好的BP神经网络对上述学习样本分别进行预测.结果如表6所示，将每个因素相同水平的5次实验结果求平均，得到各因素在不同水平情况下各指标的平均值，对同一因素不同水平的指标求最大与最小值之差，得到该因素变化所对应的极差，如表7和表8.

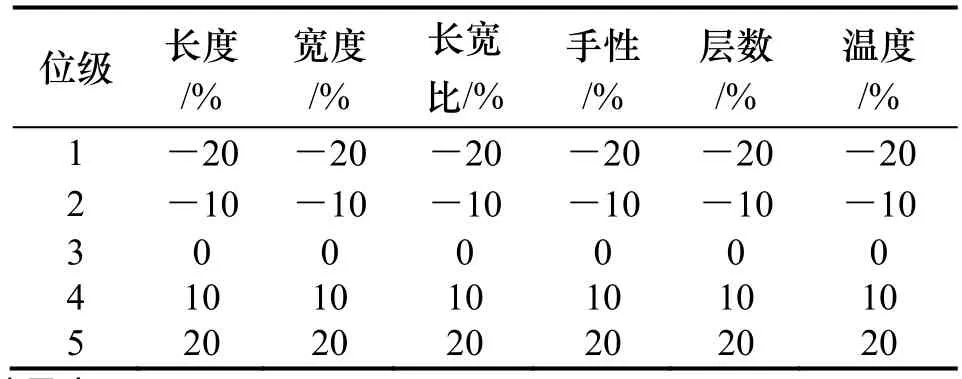
表5 因素位级表Tab.5 Factor level

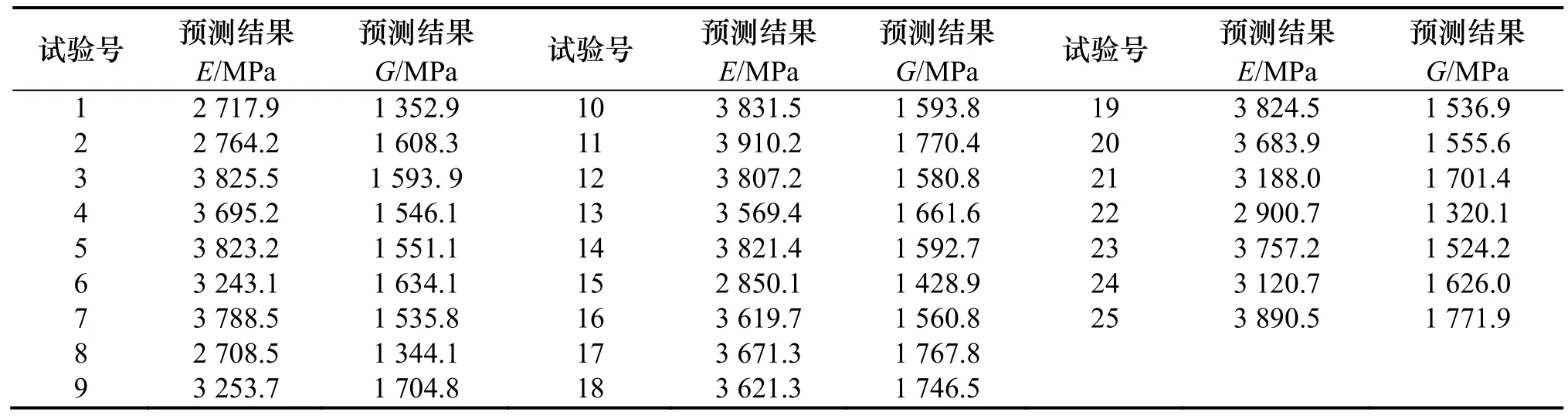
表6 预测结果表Tab.6 Prediction results

表7 正交试验结果表(E)Tab.7 The orthogonal experiment results (E)

位级 长度/nm 宽度/nm 长宽比 手性 层数 温度/K

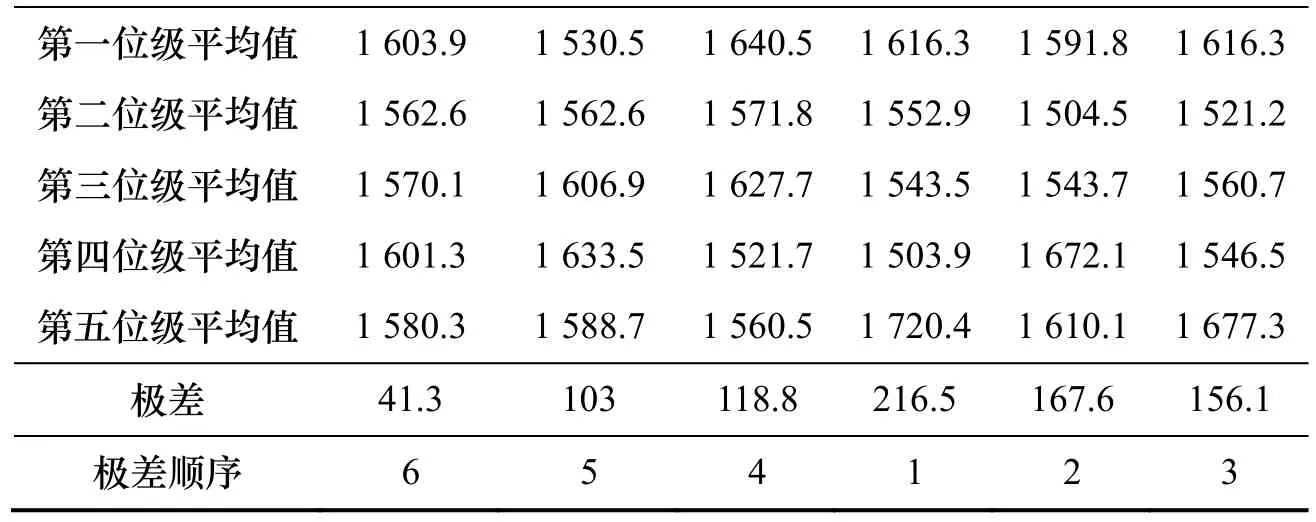
表8 正交试验结果表(G)Tab.8 The orthogonal experiment results (G)

由表7和表8可知：石墨烯薄膜弹性模量E的影响因素的灵敏性从大到小依次为手性、长度、长宽比、宽度、层数和温度.剪切弹性模量G的影响因素的灵敏性从大到小依次为手性、长宽比、温度、层数、长度和宽度.

4 结论

利用人工神经网络的BP算法对石墨烯弹性参量进行了研究.该方法有很强的函数逼近能力，应用MATLAB编程效率高，易学易懂，且计算过程迅速、方便.经研究，所建模型计算结果较准确，达到了精度要求.最后采用正交试验理论，分析了石墨烯弹性参量对各影响因素的敏感性.

(1) 人工神经网络具有大规模并行、分布式存储和良好的处理、自适应性、自组织性及很强的学习、容错和抗干扰能力等优点，将其引入到预测石墨烯薄膜的基本力学性能中，可以更全面地考虑影响石墨烯等效弹性参量的诸多因素，实现其预测的智能化.

(2) 人工神经网络建立影响石墨烯薄膜基本力学性能的各因素与其等效弹性参量之间的高度非线性映射关系，且计算过程简捷、方便，计算结果准确可靠，在较大程度上克服了实验和数值模拟方法的不足.

(3) 利用智能预测模型，验证了BP神经网络预测的 MATLAB实现是可行的，也说明该模型在石墨烯弹性参量预测方面具有适用性和可行性，为其他同类材料力学性能的预测提供了一种新的方法.

References

[1] NOVSELOW K. S., GEIM A. K., MOROZOW S. V., et al. Electric field effect in atomically thin carbon films[J].Science, 2004, (306):666-669.

[2] CORDELIA Sealy. Graphene goes from strength to strength[J]. Materials Today, 2008, 11(9):12-18.

[3] LI Peiyuan, XIE Zhijiang, LI Xinxia. Research into fault diagnosis of large rotating machinery on BP network and the data source of network[J]. Journal of Southwest University for Nationalities Natural Science Edition,2004, 30(3):386-390.

[4] SHOKRI S H M, SHOKRI E H, ROHAM Raffiee.Prediction of Young’s modulus of graphene sheets and carbon nanotubes using nanoscale continuum mechanics approach[J]. Materials and Design, 2010, 31(2):790-795.

[5] 余晓红.BP神经网络的MATLAB编程实现及讨论[J].浙江交通职业技术学院学报, 2007, 8(4):45-48.YU Xiaohong. Matlab implementation and discussion of BP neural network[J]. Journal of Zhejiang Institute of Communications, 2007, 8(4):45-48.

[6] Venkatesh. Predicting the mechanical characteristics of hydrogen functionalied graphene sheets using artificial netural network approach[J]. Journal Of Nanostructure in Chemistry, 2013, (3):83-87.

[7] 尹海莲，胡自力. 基于 BP 神经网络的复合材料性能预测[J].南京航空航天大学学报, 2006, 38(2):234-238.YI Hailian, HU Zili. Prediction of composite material properties basedon bp algorithm of artificial neutral etwork[J].Journal of Nanjing University of Aeronautics& Astronautics, 2006, 38(2):234-238.

[8] 白光辉，孟鹤松，杜善文，等.基于神经网络炭/炭复合材料烧蚀性能预测[J].复合材料学报, 2007, 26(4):83-88.BAI Guanghui, MENG HeSong, DU Shanwen, et al.Prediction on the ablative performance of carbon/carbon composites based on artificial neutral network[J]. Acta Materie Compositae Sinica, 2007, 26(4):83-88.

[9] 李东波.基于ANN的碳纤维楠竹锚杆锚固力预测研究[J].力学与实践, 2013, 35(2)：40-45.LI Dongbo. Anchorage force prediction for the cfrp-bamboo bolt based on artificial neural network[J].Mechanics in Engineering, 2013, 35(2):40-45.

[10] 王伟.人工神经网络入门与应用[M].北京：北京航空航天大学，1995.WANG wei. The introduction and application of artificial neural network[M]. Beijing: Beijing University of Aeronautics and Astronautics Press, 1995.

[11] Tho K. K., SWADDIWUDHIPONG S, LIU Z S, et al.Artificial neural network model for material characterization by indentation[J]. Modelling and Simul. Mater.Sci. Eng, 2004, 12(5):1055-1062.

[12] 朱熹育，王社良，朱军强.基于Sugeno型模糊神经网络的空间杆系结构的压电驱动器主动控制[J].工程力学, 2013, 30(8):272-277.ZHU Xiyu, WANG Sheliang, ZHU Junqiang. Sugeno type fuzzy neural network active cortrol of space frame structure based on piezoelectric actuator[J]. Engineering Mechanics, 2013, 30(8):272-277.

[13] 沈乐.石墨烯薄膜的等效弹性参数和力学行为研究[D].上海:上海交通大学大学,2010.SHEN Le. Effective elastic properties and mechanical behavior of single layer graphene sheets[D].Shanghai:Shanghai Jiao Tong University, 2010.

[14] XU Yumou, SHEN Huishen, ZHANG Chenli. Nonlocal plate model for nonlinear bending of bilayer graphene sheets subjected to transverse loads in thermal environments[J]. Composite Structures, 2013, 98(9)：294-302.

[15] 韩同伟，贺同飞，王健，等.石墨烯拉伸力学性能温度相关性的数值模拟[J].同济大学学报, 2009, 37(12)：1638-1641.HAN Tongwei, HE Pengfei, WANG Jian, et al.Numerical simulation of temperature dependence of tensile mechanical properties for single graphene sheet[J].Journal of Tongji University, 2009, 37(12)：1638-1641.

[16] 韩同伟，贺鹏飞，王健，等.单层石墨烯薄膜拉伸变形的分子动力学模拟[J].新型炭材料, 2010,25(4):261-266.HAN Tongwei, HE Pengfei, WANG Jian,et al. Molecular dynamics simulation of a single graphene sheet under tension[J]. New Carbon Materials, 2010, 25(4):261-266.