高强钢焊接薄腹矩形管截面压弯构件平面内的极限承载力

申红侠

（西安建筑科技大学土木工程学院，陕西 西安 710055）

目前建筑钢结构的发展趋势是高强度钢材的应用日益广泛，且强度水平不断提高.随着国民经济和社会的快速发展，钢结构中采用Q235和Q345级钢已不能满足实际工程的需要.高强钢不仅表现在强度上，同时具有良好的塑性、韧性、可焊性，以及其他方面的优良性能.这使得它的推广应用成为可能.屈服强度为460 MPa的Q460E钢已经成功地用于国家体育场主体结构和中央电视台新址主楼[1].高楼的转换梁和底层柱荷载很大，是高强度钢材极好的用武之地[2].澳大利亚悉尼的星城饭店柱子采用S690高强钢；日本横滨的Landmark Tower大厦采用了屈服强度为600 MPa的钢材[1].

和普通钢材相比，高强度钢构件板件宽厚比限值更小，更容易失稳，因此更易表现出局部屈曲和整体屈曲的相关性.然而，国内外对此相关屈曲的研究主要集中在高强钢轴心受压构件[3-9]，对工程中常见的压弯构件研究极少，仅文献[3]和[4]分别对11个名义屈服强度为460 MPa和3个名义屈服强度为690 MPa焊接箱形截面偏压杆进行了试验，研究其局部-整体相关屈曲，并提出强度计算公式.但该公式是一个经验性公式；文中的试件设计也不尽合理，其截面高宽比为定值0.75，翼缘的宽度大于腹板的高度，在偏心压力的作用下，翼缘先于腹板失稳，不利于充分发挥材料的性能.对单向受弯的压弯构件，为增强弯矩作用平面内的抗弯能力，常采用高而薄的腹板；为使翼缘对腹板提供约束作用，翼缘设计相对厚实.也就是说，通常放宽腹板高厚比限值，允许腹板先于构件屈曲，而不允许翼缘先屈曲.有鉴于此，本文采用ANSYS有限元软件，对名义屈服强度为460 MPa的高强钢焊接薄腹矩形管截面偏压构件的局部和整体相关屈曲性能进行研究，并研究各因素对相关屈曲极限承载力的影响，提出承载力计算公式，为高强钢的进一步推广和应用提供科学指导.

1 有限元模型及程序验证

研究对象为两端铰接等偏压构件，截面为焊接矩形管截面，弯曲轴为x轴(图1).分析中考虑了初弯曲和残余应力的影响，考虑了材料非线性和几何非线性.

图1 焊接矩形管截面和残余应力分布Fig.1 Welded rectangle tube section and residual stress distribution

初弯曲既考虑构件的整体缺陷，又考虑腹板的局部缺陷.按照钢结构设计规范GB 50017-2003[10](简称03规范)，整体初弯曲取一个正弦半波，矢高取l/1 000，l为构件长度.腹板初始几何缺陷假定为双重三角函数：

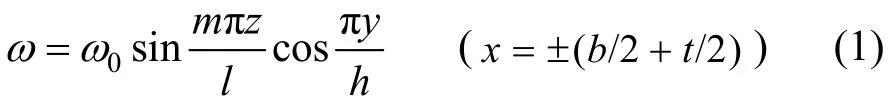
式中：ω0=h1000[5,7-9]，h为腹板高度；m=l h，为沿构件长度方向屈曲的半波数.坐标轴z沿构件长度方向；y为截面竖轴；x为截面水平轴(图1).

文献[3]测量了SM58钢(名义屈服强度460 MPa，实测屈服强度568 MPa)宽厚比b/t = 29、44、58三种试件的残余应力，得到残余拉应力峰值σrt= 0 .8fy(fy为实测屈服强度)；残余压应力均匀分布，其值σrc分别为0.32fy、0.22fy、0.15fy，其平均值为0.23fy.残余应力的分布模式如图1.图中应力拉为正，压为负.有限元分析中保持残余拉应力及其分布长度不变，残余压应力的大小及分布长度随板件宽度而变化，可按平衡条件来确定.

文献[3]实测SM58钢材料性能和普通钢材类似，故假定材料为理想的弹塑性体.材性均取实测值：fy= 568 N/mm2，E =213 000 N/mm2，ν = 0.225.

文献[8]建立有限元模型研究了高强钢方形管截面轴心受压构件的局部和整体相关屈曲性能，对该有限元模型进行修正，改变端部所施加的荷载，用于本文模拟.为了验证修正后有限元模型的正确性，先计算了文献[3]中的11个偏心受压试件.计算结果见表1.表1中试件编号E代表偏压；R和S分别代表矩形和方形管截面；其后的数字代表试件长细比；最后一个数字代表受压翼缘的宽厚比；e1和e2为偏心距.Pt是试验测得的极限承载力，Pu是有限元计算的极限承载力.经比较知，Pu/Pt最大值为1.084，最小值0.988，平均值1.039，标准差3.4%.除试件ER-65-44e2和ES-40-44e1误差稍大外，其余试件吻合较好，故文中有限元模型能够较好地模拟高强钢焊接箱形截面偏心受压构件的局部-整体相关屈曲.

表1 有限元结果和试验结果[3]比较Tab.1 Comparison of numerical and experimental results[3]

2 参数分析

采用上述有限元模型对高强钢薄腹矩形管截面偏压构件局部和整体相关屈曲进行了大量参数模拟，并分析了其相关屈曲性能以及各参数对极限承载力的影响.计算中板件厚度t=4mm保持不变.材料和残余应力分布同上.根据03规范[10]，箱形截面翼缘宽厚比限值=28.6；腹板高厚比限值与应力梯度和长细比有关，是一个变量.本文在计算中翼缘宽厚比不超限，仅腹板高厚比超限，故取翼缘宽厚比b/t = 20、24、28，腹板高厚比h/t = 40、50、60、70.构件长细比λ = 20、40、60、80、100、120，偏心率ε = e/(W/A) = 0.2、0.4、0.6、0.8、1.0、1.5、2.0、2.5、3.0、4.0(e为偏心距，W为毛截面模量，A为毛截面面积).下文是对有限元模拟结果分析.

2.1 荷载-位移曲线

图2给出b/t = 24、h/t = 50，ε = 0.4、0.8、1.0、2.0、3.0和4.0时在不同长细比情况下的轴向压力P和压缩变形Uz曲线.试验[3-5]中往往是试件先发生局部屈曲，随后发生整体屈曲.和试验现象不同，有限元分析中由于存在初始几何缺陷，从一开始加载整体弯曲变形和局部弯曲变形同时发生.随着荷载增加，两种弯曲变形不断增加，彼此互相影响.

由图2可知，荷载-变形曲线由两部分组成：上升段和下降段(有些曲线由于人为终止计算或发生屈曲而突然破坏使得下降段不明显).有时在极值点之后会出现下降段向原点方向“漂移”的现象，如图2(b)中λ=60和80、图2(c)中λ=60和图2(e)中λ=100等.这可能是由于不适当的弧长半径引起的，但它不会影响构件的极限承载力.和高强钢方形管截面轴心受压构件局部和整体相关屈曲的荷载-位移曲线[8]不同，高强钢薄腹矩形管截面压弯构件的荷载-变形曲线往往有相对较陡的下降段，有时甚至在有限元模拟中由于发生屈曲导致较大位移而破坏.由图2还可以发现，随着长细比的增大，高强钢薄腹矩形管截面压弯构件的极限承载力和起始刚度均降低了，但腹板屈曲后强度保持能力和构件的延性却提高了.

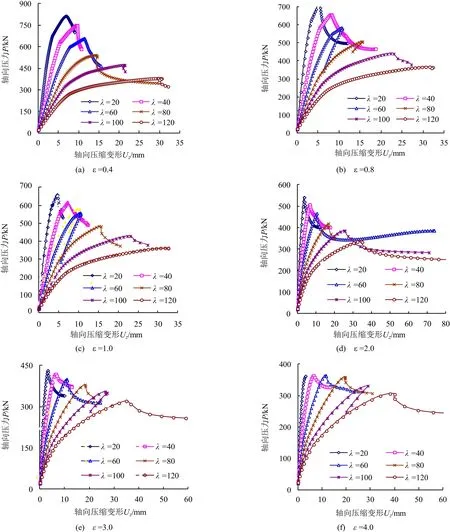
图2 轴向压力-轴向压缩变形曲线(b/t=24, h/t=50)Fig.2 Axial compressive force versus compressive deformation curves (b/t=24, h/t=50)

2.2 各参数对极限承载力的影响

2.2.1 长细比

图3是b/t =28，h/t = 40和70时高强钢压弯构件无量纲极限承载力Pu/(Afy)随长细比λ的变化曲线.fy取实测屈服强度568 MPa，以下相同.需要说明的是由于腹板初始几何缺陷沿构件长度方向屈曲的半波数必须为整数，有限元分析中构件长度取值并非计算长度，而是在保证屈曲半波数为整数的条件下和计算长度最接近的一个数值，故文中长细比λ = 20、40、60、80、100和120只是名义长细比，实际长细比并非这些整数.图3中采用实际长细比.同腹板高厚比未超限者不同，Pu/(Afy)和λ近似为直线关系.随着λ增大，Pu/(Afy)不断减小，并且随着偏心率ε增大，这种变化趋势逐渐变缓，当ε = 4.0时甚至接近水平线.这些均和文献[11]中腹板高厚比超限的普通钢工字形偏压构件的曲线变化趋势类似，再次证明了有限元模型的正确性.

图3 Pu/(Afy) -λ曲线(b/t=28)Fig.3 Pu/(Afy) -λ curves(b/t=28)

2.2.2 高厚比

图4为长细比λ=60，b/t=20和28时极限承载力Pu/(Afy)随腹板高厚比h/t的变化关系.由图4知，h/t和Pu/(Afy)之间为曲线关系，但非线性并不是很明显，为简单起见，可近似为线性关系；随着h/t增大，Pu/(Afy)逐渐降低.原因是随着高厚比增大，即截面高度增大，导致局部几何缺陷增大；另一方面，截面高度增大使得回转半径增大，而长细比不变，构件长度会增大，导致整体几何缺陷增大.几何缺陷和构件长度的增大使得构件极限承载力Pu/(Afy)下降.

图4 Pu/(Afy) -h/t曲线(λ = 60)Fig.4 Pu/(Afy) -h/t curves(λ = 60)

2.2.3 宽厚比

图5给出长细比λ=60，h/t=50和60时极限承载力Pu/(Afy)随翼缘宽厚比b/t的变化情况.图5(a)中b/t=24构件计算长度应大于b/t=20构件，但为使腹板屈曲半波数为整数，在计算中取相同长度，故使构件b/t=24极限承载力略为大于b/t=20的极限承载力.略去这些，总体变化趋势是：随着b/t增大，Pu/(Afy)缓慢降低；b/t和Pu/(Afy)之间也近似为线性关系.可能的原因是随着b/t增大，即截面宽度增大，翼缘对腹板的约束作用减弱，进而导致极限承载力Pu/(Afy)下降.对比图4和图5还可看出，翼缘宽厚比的变化对高厚比超限的高强钢压弯构件极限承载力Pu/(Afy)的影响远不如腹板高厚比变化影响大.

图5 Pu/(Afy) -b/t曲线(λ = 60)Fig.5 Pu/(Afy) -b/t curves (λ = 60)

2.2.4 偏心率

偏心率ε反映了弯矩和轴力之间的比例关系，偏心率小意味着弯矩较小，轴力起主导作用，相反，偏心率大则弯矩起主导作用.由图3知，长细比λ对轴力起控制作用的压弯构件影响较大，而对弯矩起控制作用的构件则影响不大.图4和图5中偏心率变化对曲线的变化趋势几乎无影响，这说明腹板和翼缘对构件的承载力轴力项和弯矩项均有贡献.

2.3 弯矩-轴力相关曲线

弯矩与轴力的相关关系式是反映压弯构件在弯矩与轴力共同作用下受力性能的重要表达式.三种不同宽厚比薄腹矩形管截面压弯构件的Pu/Py和Mu/My相关曲线的变化趋势基本相同.图6给出了b/t=28，h/t=50和70时Pu/Py和Mu/My相关曲线.图6中Mu=Pue，Py=Afy，My=Wfy.由图6可知，高强钢薄腹矩形管截面压弯构件的Pu/Py和Mu/My相关曲线总体变化趋势为直线关系.当λ=20时，Pu/Py和Mu/My曲线(h/t=50)略为向上凸或近似为直线(h/t=70)；其余相关曲线(λ = 40、60、80、100、120)则略为下凸.但这种变化趋势远小于腹板高厚比未超限的普通钢压弯构件.

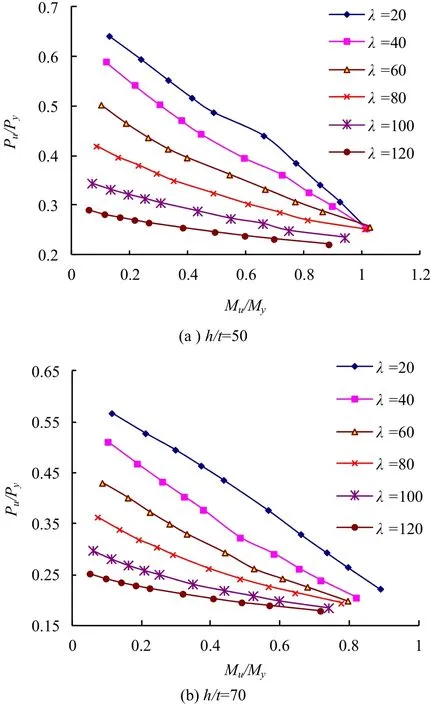
图6 薄腹矩形管截面压弯构件的Pu/Py和Mu/My相关曲线(b/t=28)Fig.6 Interactive curves between Pu/Py and Mu/My of thin-webbed rectangular tube section beam-columns (b/t=28)

3 高强钢薄腹矩形管截面压弯构件平面内稳定计算公式

弯矩与轴力的相关关系式是推导压弯构件稳定计算公式的重要依据.高强钢薄腹矩形管截面压弯构件的Pu/Py和Mu/My相关关系近似为直线关系；文献[12]研究表明，线性的相关关系能很好地预测名义屈服强度为240 MPa中等长细比双向受弯薄腹工字形截面压弯构件的极限承载力.因此，按边缘纤维屈服准则推导的公式(即式(2))来确定本文计算公式.

式中：N为构件轴向压力；Mx为弯矩；βmx为等效弯矩系数，对两端等弯矩作用，βmx=1.0；φx为轴心受压构件绕强轴失稳的稳定系数； W1x为对受压纤维的截面模量； NE′x=π2EA/ ( 1.1λx2)，本文中λx= λ；fy为钢材实测屈服强度.

式(2)用于计算腹板高厚比未超限普通钢压弯构件.若将其用于计算高强钢薄腹矩形管截面压弯构件，还需进一步修正.修正后的公式为式(3).

式中：φx由λ按b类截面查表[10]；α为屈服强度修正系数.

令N = Nu=Pu，Mx= Mu= Pue ，将有限元计算结果Pu代入式(3)，由左端项比屈服强度 fy得修正系数α.由前述分析知，腹板高厚比超限高强钢压弯构件极限承载力与构件长细比λ、腹板高厚比h/t、翼缘宽厚比b/t和相对偏心率ε有关；无量纲极限承载力Pu/(Afy)与λ、h/t和b/t中的每一个量近似为线性关系；偏心率ε的影响虽然在式(3)第二项中有所反映，但从α值变化来看一般是ε越大α值越大.因此，为方便应用，屈服强度修正系数α可看作这四个变量的一个线性函数.考虑到短柱(λ=20)以局部屈曲为主导变形，长柱(λ=120)以整体屈曲为主导变形，去掉这两组数据，对其余480个计算结果进行拟合，得：

在翼缘宽厚比未超限时，其对极限承载力的影响很小，可忽略不计.重新对数据进行拟合，得：

经比较，式（4）和式（5）计算结果基本相同.考虑到式(5)只有50%的保证率，将其值减去两倍标准差，得：

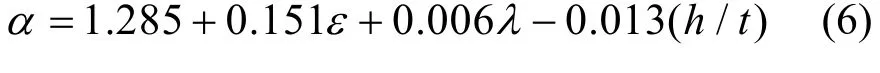
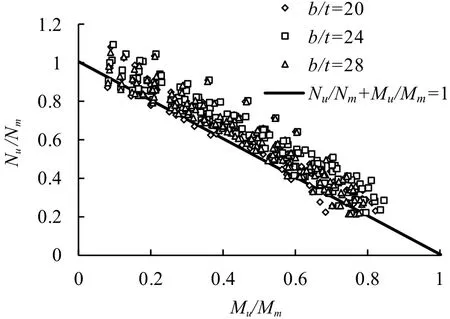
um图7 式(3)与有限元结果对比Fig.7 Comparison of formula (3) with numerical results

4 结论

(1) 考虑初弯曲和残余应力影响的双重非线性有限元模型能够很好地模拟高强钢焊接箱形截面偏心受压构件的局部-整体弯曲相关屈曲.

(2) 高强钢薄腹矩形管截面压弯构件平面内无量纲化极限承载力Pu/(Afy)与构件长细比、腹板高厚比和翼缘宽厚比近似为线性关系.偏心率较小时，长细比增大，Pu/(Afy)值下降较快，而偏心率较大时，Pu/(Afy)随长细比增大下降变缓.随着高厚比的增大，Pu/(Afy)值下降较快，而随宽厚比增大，却下降缓慢，且这种变化趋势不随偏心率的变化而变化.在翼缘宽厚比未超限的情况下，可忽略其对承载力的影响.

(3) 高强钢薄腹矩形管截面单向压弯构件的轴力和弯矩相关曲线近似为直线.

(4) 按边缘纤维屈服准则推导的公式经过修正之后可用于计算名义屈服强度为460 MPa高强钢压弯构件局部-整体弯曲屈曲的极限承载力.修正公式的计算值与有限元模拟结果吻合良好.公式适用的范围为翼缘宽厚比未超限的薄腹矩形管截面.

References

[1] 石永久. 高强度和高性能钢材在建筑结构中的应用和发展[C]//第三届结构工程新进展国际论坛文集. 北京:中国建筑工业出版社, 2009: 397-407.SHI Yongjiu. Development and application of high strength and high performance steel in buildings[C]//the 3rd International Forum on Advances in Structural Engineering. Beijing: China Architecture & Building Press,2009: 397-407.

[2] 陈绍蕃, 申红侠. 热轧高强度钢压杆的承载能力分析[J]. 建筑钢结构进展, 2011, 13(4): 1-5.CHEN Shaofan, SHEN Hongxia. Analysis of the load-carrying capacity of hot-rolled high-strength steel struts[J]. Progress in Steel Building Structures, 2011,13(4): 1-5.

[3] USAMI T, FUKUMOTO Y. Welded box compression members[J]. Journal of the Structural Engineering, 1984,110(10): 2457-2470.

[4] USAMI T, FUKUMOTO Y. Local and overall buckling of welded box columns[J]. Journal of the Structural Division, 1982, 108(ST3): 525-542.

[5] DEGÉE H, DETZEL A, KUHLMANN U. Interaction of global and local buckling in welded RHS compression members[J]. Journal of Constructional Steel Research,2008, 64(7-8): 755-765.

[6] 陈绍蕃. 焊接薄壁箱形截面轴心压杆的承载力计算[J].建筑钢结构进展, 2009, 11(6): 1-7.CHEN Shaofan. Capacity calculation of welded axially compressed members with thin-walled box section[J].Progress in Steel Building Structures, 2009, 11(6): 1-7.

[7] SHEN Hongxia. Ultimate capacity of welded box section columns with slender plate elements[J]. Steel and Composite Structures, 2012, 13(1): 15-33.

[8] 申红侠. 高强度钢焊接方形截面轴心受压构件的局部和整体相关屈曲[J]. 工程力学, 2012, 29(7): 221-227.SHEN Hongxia. Local-overall interaction buckling of high strength steel welded square box columns[J]. Engineering Mechanics, 2012, 29(7): 221-227.

[9] 申红侠. 宽厚比超限的高强钢方形截面轴心受压构件的极限承载力[J]. 建筑结构, 2012, 42(11): 119-122.SHEN Hongxia. Ultimate capacity of high-strength steel square box columns with large plate width-to-thickness ratio[J]. Building Structure, 2012, 42(11): 119-122.

[10] GB 50017-2003 钢结构设计规范[S]. 北京: 中国计划出版社, 2003.GB 50017-2003 Code for design of steel structures[S].Beijing: China Planning Press, 2003.

[11] 顾强. 腹板宽厚比超限时I形截面偏压杆平面内的承载力[D]. 西安: 西安冶金建筑学院, 1988.GU Qiang. In-plane ultimate capacity of I-section columns with slender web subjected to eccentric compression[D]. Xi'an: Xi'an Institute of Metallurgy and Construction Engineering, 1988.

[12] SALEM A H, EL AGHOURY M, EL DIB F F, et al.Strength of bi-axially loaded slender I-section beam-columns[J]. Canadian Journal of Civil Engineering,2007, 34(2): 219-227.