单轴对称圆孔蜂窝梁弯扭屈曲承载力的简化计算

陈向荣，陈 星

（西安建筑科技大学土木工程学院，陕西 西安710055）

蜂窝梁在整体失稳时表现为弯扭屈曲，截面的不对称性势必会加剧蜂窝梁的侧倾程度；初始缺陷的存在，又将降低无足够侧向支撑蜂窝梁的弯扭屈曲承载力，其中残余应力的影响尤为显著，因此在分析计算整体稳定承载力时，须考虑初始缺陷的影响[1-3]. 国内学者未曾研究过存在初始缺陷的单轴对称蜂窝梁的弯扭屈曲性能，对今后蜂窝梁的发展及推广使用不利，故有必要进行研究.

采用ANSYS建立文献[9]中的试验模型，对考虑材料非线性和几何非线性的有限元模型进行验证，在两者结果相差不大的情况下，探寻残余应力对不同孔高比、距高比及跨高比的单轴对称圆孔蜂窝梁（以下未加说明的“蜂窝梁”均为“单轴对称圆孔蜂窝梁”）弯扭屈曲性能的影响，同时将有限元算得的弯扭屈曲载与我国规范公式算出的当量单轴对称实腹梁的弯扭屈曲荷载比较，发现二者具有相关性，经非线性回归分析，提出单轴对称圆孔蜂窝梁弯扭屈曲荷载的简化计算公式.

1 试件设计

单轴对称圆孔蜂窝梁所用的钢材为 Q345，弹性模量 E = 2.06×105N / mm2，泊松比 υ = 0.3. 业内较为广泛使用的蜂窝梁设计参数是孔高比、距高比和跨高比，其中孔高比是指孔洞与蜂窝梁梁高之比，距高比是指孔间距与蜂窝梁梁高之比，跨高比即是跨度与蜂窝梁梁高之比. 由于这三个参数即可全面确定一根蜂窝梁的尺寸，故下文将以这三个研究参数展开对跨中承受集中荷载的蜂窝梁整体稳定性的探究.

1.1 研究参数的取值范围

蜂窝梁开孔过小对原型梁的承载力提高较少，开孔过大将过分削弱截面；距高比过小会导致应力集中现象较为显著，过大会降低材料利用率；跨高比会随着实际工程中梁的跨度不同而变化. 因此设定蜂窝梁的孔高比的选取范围：0.4～0.8，梯度为0.05；距高比的选取范围：0.2～0.8，梯度为0.1；跨高比的选取范围：12～28，梯度为2.

1.2 试件尺寸设计

单轴对称工字钢圆孔蜂窝梁的原型梁采用国产热轧型钢梁HM150×100，其中上翼缘宽度由100 mm改为150 mm，其他尺寸不变，分别选取三个参数的变化范围，制成的单轴对称圆孔蜂窝梁的尺寸如图1所示，由于试件较多，仅列出部分试件的尺寸，见表1.

1.3 残余应力模型

构件纵向残余应力的分布和大小与截面的形状和尺寸、轧制和焊接工艺及材料性能等诸多因素有关，许多国家曾采用锯割法测定了残余应力，通过统计分析拟定了典型的残余应力分布图[4]，但对于单轴对称截面残余应力分布模式的研究较少.Kitipornchai S曾用剑桥大学工作组提出的单轴对称钢梁残余应力模型（简称TF模型）做了试验研究，证明此分布模型与试验结果相吻合[5]. 哈工大的张壮南博士用截面法测定了单轴对称工字梁的残余应力，所得整体残余应力分布形式与剑桥大学工作组所提出的模型相近，但由于测点与切割面较远，残余应力峰值较小[6]，故本文中残余应力分布采用TF模型，其分布如图2所示.

其中，拉应力区残余应力分布长度Cf=F/(σy+σfc)(2tf+tw),压应力区残余应力峰值 σfc= F /bf(tf+0.5tw),腹板内残余压应力峰值 σwc=2 Cfσy/HwCf；构件内由于焊接过程引起的约束力 F= BAw,焊接常数B=8kN/mm2,A是焊接区域的面积.

w

表1 部分单轴对称圆孔蜂窝梁尺寸表 /mmTab.1 Size table of partial monosymmetric cellular beams /mm

图1 单轴对称圆孔蜂窝梁的构件截面示意图Fig.1 Section diagram of monosymmetric cellular beams

2 有限元模型的建立与验证

2.1 有限元模型简介

钢材本构关系采用理想弹塑性模型，遵从Von.Mises屈服准则. 采用SHELL181壳体单元，忽略厚度方向的变形和应力. 考虑到孔洞边缘应力集中引起的复杂应力状态，腹板采用三角形单元，翼缘采用四边形单元，单元边长均为10 mm.

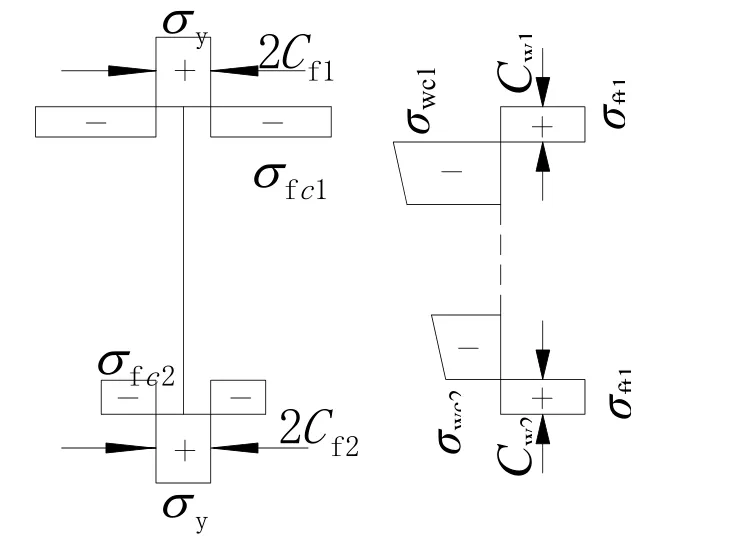
图2 单轴对称圆孔蜂窝梁残余应力分布及大小Fig.2 Residual stress distribution and magnitude of monosymmetric cellular beams

构件端部使用夹支型支座，端部仅可自由翘曲、绕x轴和y轴转动，不能绕z轴转动，也不能侧向移动.建模时，约束梁一端下翼缘三个方向线位移和另一端下翼缘的侧向及竖向位移，禁止梁两端上翼缘发生侧向位移[7].

2.2 在模型中加入初始缺陷

初始缺陷的存在会降低梁的稳定承载力，在整体稳定分析时需要考虑几何缺陷和残余应力的影响.先建立无初始缺陷的模型，在跨中截面上翼缘处施加单位集中力，进行特征值屈曲，得到一阶屈曲模态，见图 3；加入几何缺陷，编写 FORTUNE语句对模型施加残余应力，求解模型得到初应力文件；最后用 ISFILE命令读入初应力文件，用弧长法进行大变形计算，得出整体稳定承载力[8].

2.3 有限元模型正确性验证

目前单轴对称蜂窝梁的弯扭屈曲承载力没有相关解析公式进行计算和参考，也没有学者研究过相关性能，试验资料匮乏，故有限元的分析部分将成为文章的重要支撑，必须保证有限元模型的精确性.为验证所建双重非线性ANSYS模型的仿真程度，建立文献[9]中选出的三根考虑双重非线性的双轴对称圆孔蜂窝梁，并与文献[9]中所得弯扭屈曲荷载对比，结果见表2.可见与其弯扭屈曲荷载相近，误差在5 %以内，且比原文的有限元模型所得结果

更贴近试验值，从而证明此模型的有效性和正确性.

图3 蜂窝梁的一阶屈曲模态Fig.3 First yield mode of cellular beams

表2 有限元模型验证试件表Tab.2 The specimen sizes table of finite element model validation

3 残余应力对弯扭承载力的影响

图4为采用TF残余应力分布的梁纵向应力云图，蜂窝梁板件交接处残余应力为拉应力，翼缘及腹板中部为压应力. 因存在残余应力，梁产生结构变形，但最大挠度很小，量级仅为10-15mm.

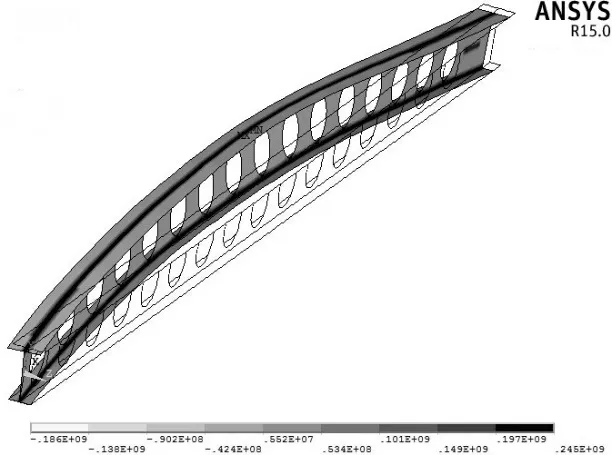
图4 施加残余应力后的梁纵向应力云图及变形Fig.4 Stress map and deformed shape of cellular beam with residual stress

图5 -图7为孔高比、距高比、跨高比不同的情况下，同时加入几何缺陷、残余应力与仅加入几何缺陷的弯扭屈曲承载力对比. 在考虑一个因素的影响时变化另两个因素，以查看不同情况下单一因素影响变化趋势是否唯一. 从图中可以看出，三个因素对残余应力影响的变化趋势均基本不变，证明三个因素对有残余应力的梁具有一致的变化规律，可进一步分析.取部分具有代表性的数值点列于表3.

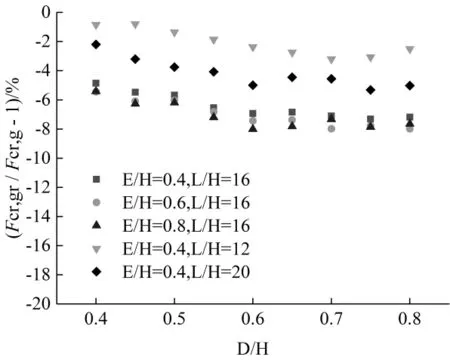
图5 残余应力对不同孔高比蜂窝梁的影响Fig.5 Influence of residual stress on cellular beams with varied Opening-Height Ratio

图5 中，孔高比从0.4不断增加时，腹板削弱程度增大，残余应力的影响逐渐增加，但影响的变化幅度仅在2 %之内. 图6可见，距高比增加，对残余应力影响的幅度保持在1 %之内因此对于另两个参数确定、孔高比或距高比不同的单轴对称圆孔蜂窝梁，残余应力对弯扭承载力影响的变化不大.

图7表明跨高比增加时，残余应力对蜂窝梁弯扭屈曲承载力影响的变化较为显著，两者呈现接近正比的关系，由此可判定跨高比是确定残余应力对蜂窝梁弯扭屈曲承载力影响变化幅度的主要因素.

综上，在设计较大跨高比单轴对称圆孔蜂窝梁时，须考虑残余应力影响，否则设计值偏大，使蜂窝梁未达强度极限就发生整体失稳不能继续服役.

图6 残余应力对不同距高比蜂窝梁的影响Fig.6 Influence of residual stress on cellular beams with varied Pitch-Height Ratio

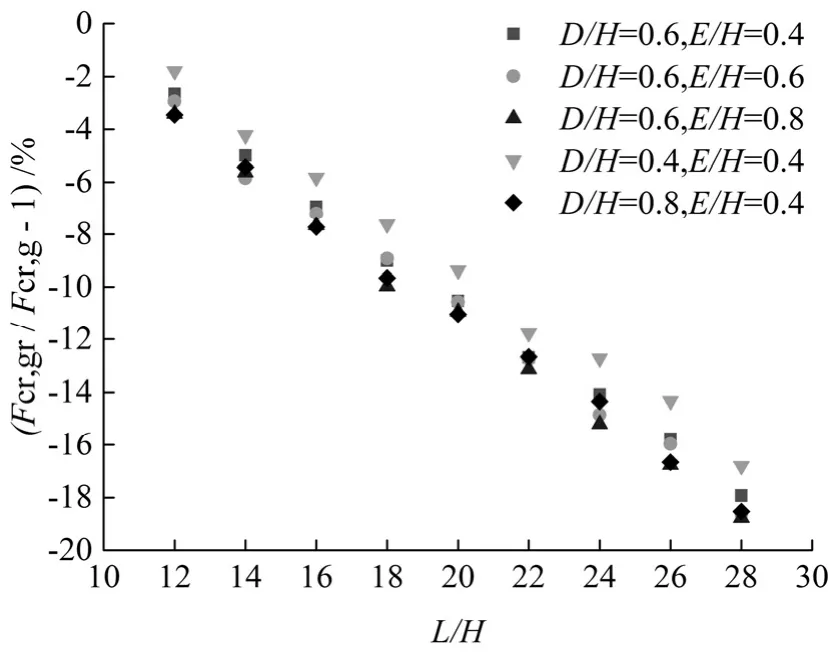
图7 残余应力对不同跨高比蜂窝梁的影响Fig.7 Influence of residual stress on cellular beams with varied Length-Height Ratio

表3 有限元结果及规范公式计算结果的对比Tab.3 Comparison between FEM results and calculated results with standard calculation

4 考虑双重非线性的弯扭屈曲承载力简化算法

基于第三节的结论，利用ANSYS建立双重非线性有限元模型，对不同孔高比、距高比和跨高比的单轴对称圆孔蜂窝梁进行弯扭屈曲分析，经过对结果的观察，发现所有试件都是弯扭屈曲破坏，未发现腹板有局部屈曲的现象，屈曲形式如图8所示.

4.1 弯扭屈曲承载力折减系数ψ

图8 单轴对称圆孔蜂窝梁的截面弯扭形式Fig.8 Lateral buckling shape of monosymmetric cellular beams’ section

通过有限元分析，发现单轴对称圆孔蜂窝梁与当量单轴对称实腹梁的弯扭屈曲承载力存在某种特定的联系.为此笔者提出单轴对称圆孔蜂窝梁弯扭屈曲承载力的折减系数 ψ =Fcr,cell/Fcr,solid，其中Fcr,cell为有限元分析所得单轴对称圆孔蜂窝梁的弯扭屈曲承载力， Fcr,solid为使用陈骥前辈的《钢结构稳定理论》[5]与GB50017-2003[10]中单轴对称工字梁公式算得的当量单轴对称实腹梁弯扭屈曲承载力.

4.2 孔高比、距高比和跨高比与ψ的关系

将 Fcr,cell和 Fcr,solid用ψ表示，通过参数分析，得出图9-图11中孔高比、距高比和跨高比与ψ的关系.研究单一因素与ψ的关系时，为排除其他两个因素的干扰，验证所得规律的正确性，分别改变另两个参数，观察变化趋势的一致性.从图中所得结果可以看出，在另两个参数改变的情况下，ψ的变化趋势没有大的浮动，其他因素的改变并没有干扰到单一因素与ψ关系曲线的形状，因素之间的相关性可以忽略.表3为抽取出具有代表性模型的计算结果、规范所得结果及两者差值百分比.

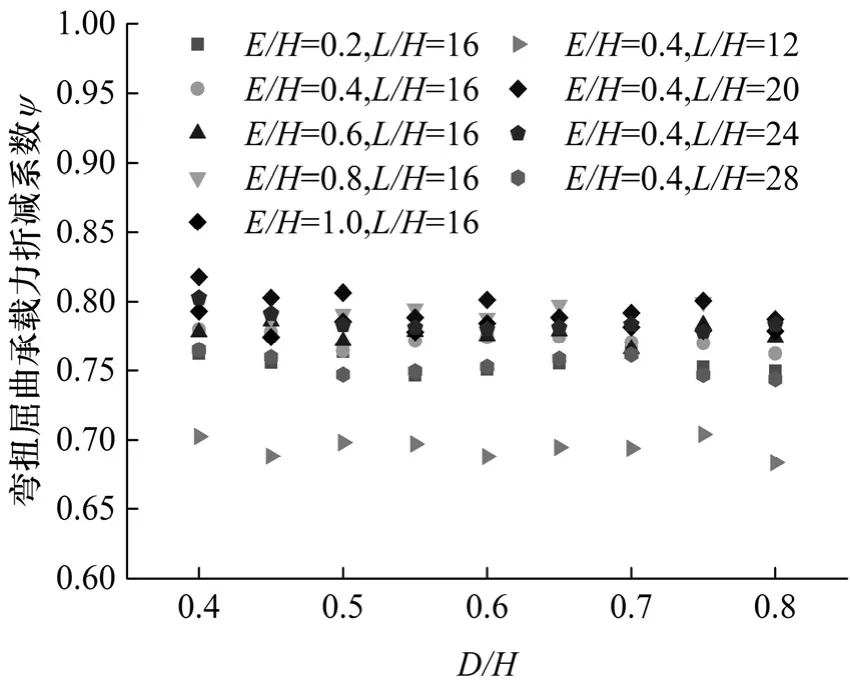
图9 孔高比与弯扭屈曲承载力折减系数ψ的关系Fig.9 Relations between Opening-Height Ratio and lateral buckling resistance reduction factor ψ

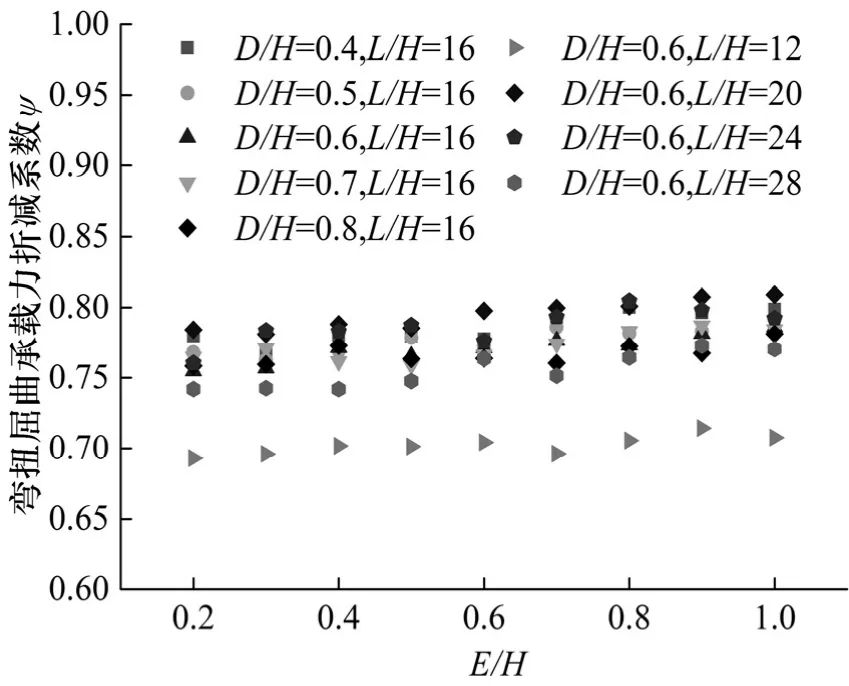
图10 距高比与弯扭屈曲承载力折减系数ψ的关系Fig.10 Relations between Pitch-Height Ratio and lateral buckling resistance reduction factor ψ

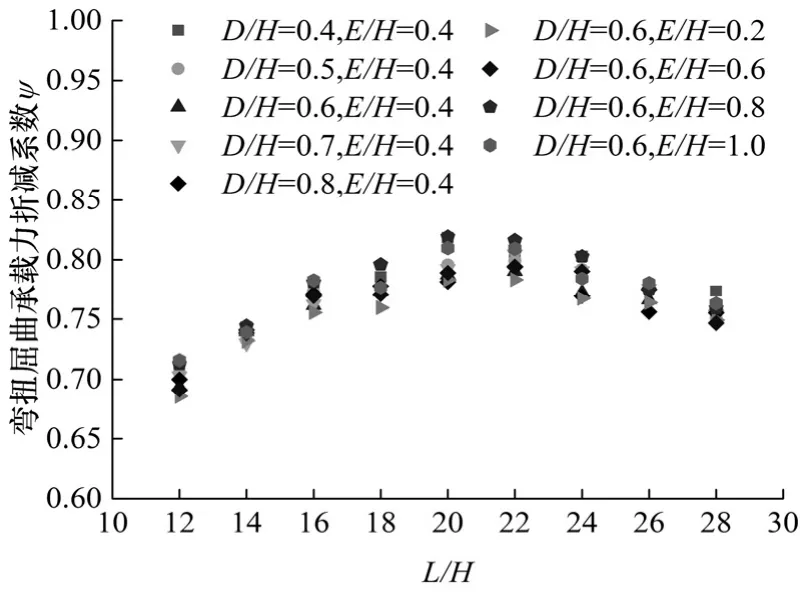
图11 跨高比与弯扭屈曲承载力折减系数ψ的关系Fig.11 Relations between Length-Height Ratio and lateral buckling resistance reduction factor ψ

表3及图9表明当孔高比变化时，ψ的变化较波折，但浮动不大，在未要求精确计算的情况下，可以忽略不计.

表3及图10中，改变距高比将使ψ有轻微上扬的趋势，因此距高比增大对稳定性能有贡献，但ψ的变化并不显著，计算时可稍加考虑.

表3及图11中，跨高比与ψ的关系很明朗，ψ在 0.65～0.85之间变化，关系曲线呈倒开口形态的二次抛物曲线；跨高比小于16时ψ较小，说明跨高比较小的蜂窝梁比当量实腹梁的弯扭屈曲荷载小很多；跨高比在18～24之间时ψ较大，说明跨高比在此范围内的蜂窝梁有较高的弯扭屈曲荷载；跨高比大于24时，ψ有所降低，表明跨高比较大的蜂窝梁无法获得足够的弯扭屈曲承载力提高. 因此，在设计蜂窝梁时，可尽量选取跨高比在18～24之间的蜂窝梁，用较少的材料获得较高的弯扭承载力.

4.2 弯扭屈曲承载力简化计算式

为简化计算，不使用高阶计算式，拟采用二次多项式作为ψ的计算公式模型.

ψ随着跨高比增大的变化最显著，随着距高比增加有较为规律的变化，因此可利用Origin 8.5先对其中一种距高比蜂窝梁的L/H-ψ关系曲线进行非线性回归分析得出初步计算式，再充分考虑距高比对ψ的影响修正计算式，即可得到较为精确的计算式，最终通过ψ的定义式可得单轴对称圆孔蜂窝梁弯扭屈曲承载力cell,crF 的简化计算公式：

4.3 弯扭屈曲承载力简化计算式的验证与评价

为验证所得计算式的正确性，随机指定五根单轴对称圆孔蜂窝梁的尺寸参数，用有限元软件模拟得到有限元解，用上式简化计算这五根梁弯扭屈曲承载力的解析解，结果对比见表4.

从表4中可以看出，用上式算得的弯扭屈曲承载力与有限元所得弯扭屈曲承载力十分接近，两者相差在3 %左右，且用上式计算的结果均低于有限元结果，在一定程度上保守地计算弯扭屈曲承载力.因此可以将上式作为单轴对称圆孔蜂窝梁的弯扭屈曲承载力简化计算公式，此简化设计方法可为设计提供方便，减少设计周期，具有较高的安全度.

表4 单轴对称圆孔蜂窝梁弯扭屈曲承载力简化计算式的验证结果Tab.4 Identified results of simplified lateral buckling resistance calculation of monosymmetric cellular beam

5 结论

在大量参数研究的基础上，通过数据处理和非线性回归分析，得出以下结论：

（1）通过 ANSYS模拟文献[9]中的双轴对称圆孔蜂窝梁，采用本文所建加入几何缺陷和残余应力的双重非线性有限元模型计算得到的蜂窝梁弯扭屈曲荷载比原文中的模型更接近试验结果.

（2）残余应力对孔高比、距高比变化的单轴对称圆孔蜂窝梁弯扭屈曲承载力影响较小，变化幅度在2 %之内；残余应力对跨高比变化的构件影响较大，随着跨高比增加，其影响趋近于正比增大.在设计单轴对称圆孔蜂窝梁时必须考虑残余应力的影响，否则会使计算结果偏大，结构可靠度降低.

（3）为量化单轴对称圆孔蜂窝梁与当量单轴对称实腹梁的弯扭屈曲荷载的关系，同时利用此关系简化设计计算过程，提出单轴对称圆孔蜂窝梁弯扭屈曲承载力折减系数ψ.研究孔高比、距高比及跨高比变化对ψ的影响，发现孔高比的变化对ψ的影响不大；距高比增大时，ψ值有小幅上升；跨高比增加时，ψ值呈现倒开口二次抛物曲线的形态，对数值点进行非线性回归分析，得出ψ关于跨高比的关系式，在此基础上引入距高比对ψ的影响对上述计算式进行修正，得出单轴对称圆孔蜂窝梁弯扭屈曲承载力的简化计算公式.

（4）验证结果表明提出的单轴对称圆孔蜂窝梁弯扭屈曲承载力的简化计算公式具有足够的精确性和可靠性，在设计中可以参考和应用.

References

[1] LIU T CH, CHUNG K F.Steel beams with large web openings of various shapes and sizes finite element investigation[J].Journal of Constructional Steel Research, 2001,57(1): 1159 -1176.

[2] 陈绍蕃.单轴对称工形截面无支撑简支梁的稳定承载能力[J]. 钢结构, 2008, 23(08): 14-19.CHEN Shaofan. Buckling capacity of unbraced simplysupported beams with monosymmetric I-section[J]. Steel Structure, 2008, 23(08): 14-19.

[3] SRITAWAT KITIPORNCHAI, ALAIN D. Wong Chung.Inelastic buckling of welded monosymmetric I-beams[J].Journal of Structural Engineering, 1987, 113(4): 740-756.

[4] SWEEDAN, AMR M I. Elastic lateral stability of I-shaped cellular steel beams[J]. Journal of Constructional Steel Research, 2011, 67(2): 151-163.

[5] 陈骥.钢结构稳定理论与设计[M].第5版.北京: 科学出版社, 2011.CHEN Ji. Stability theory and design of steel construction[M]. 5th. ed. Beijing: Science Press, 2011.

[6] 张壮南, 张耀春.残余应力对单轴对称工字梁稳定承载力的影响[J].哈尔滨工业大学学报, 2007, 39(12):1864-1868.ZHANG Zhuangnan, ZHANG Yaochun. Effects of welding residual stresses on the stability capacity of the monosymmetric I-beams[J]. Journal of Harbin Institute of Technology, 2007, 39(12): 1864-1868.

[7] 张利若, 陈绍蕃, 顾强.工形截面纯弯曲梁翼缘腹板的相关屈曲[J].西安建筑科技大学学报:自然科学版,1996,28(4):86-91.ZHANG Liruo, CHEN Shaofan, GU Qiang. Interaction of local buckling in welded I-section steel beams[J]. J. Xi'an Univ. of Arch. & Tech. (Natural Science Edition), 1996,28(4): 86-91.

[8] FU dingfa, ZHOU changqing, LI can. Effect of welding sequence on residual stress in thin-walled octagonal pipe-plate structure[J]. Transactions of Nonferrous Metals Society of China, 2014, 24(3): 657-664.

[9] DELPHINE S, JAN B. Lateral-torsional buckling resistance of cellular beams[J]. Journal of Constructional Steel Research, 2015, 105(10): 119-128.

[10] 中华人民共和国建设部. GB50017-2003钢结构设计规范[S]. 北京: 中国计划出版社, 2003.Ministry of Development of the People’s Republic of China.GB50017-2003 Code for design of steel structures[S]. Beijing: China Planning Press, 2003.