基于模糊语言算子的工程项目施工可靠性评价研究

史玉芳，王秀芬，康 珅

（西安科技大学管理学院， 陕西 西安 710054）

可靠性理论是近年来管理科学领域的研究热点，它是一门涉及众多领域的交叉性学科，广泛应用于生产制造、机械、航空、航天、土木建筑等领域.在建筑领域，关于可靠性方面的研究主要限于结构工程方面，在施工管理领域仍处于探索阶段[1].工程项目施工系统与上述传统可靠性应用领域如航天、航空及制造业生产系统等具有一定的相似性，施工流程与其他生产制造系统中的生产工艺流程一样都具有错综复杂的逻辑关系.因此，也可以用可靠性来研究施工管理问题.

尽管施工可靠性并没有作为一个专门的工程项目管理研究问题被提出，但实际上很早以前与之有关的很多施工管理工作早已被重视和研究，如工艺技术可靠性研究、工程项目施工方法可靠性研究等，都属于技术层面的可靠性分析，但未体现工程项目的施工目标管理要求.上个世纪八十年代，前苏联学者 C·A·乌沙茨基提出了反映流水施工质量的可靠性指标，对流水施工系统可靠度进行了计算[2].截止目前，广泛运用于工程项目进度管理的网络计划，如GERT、PERT、VERT、QGERT等这些网络计划技术，均运用了概率方法进行施工进度可靠性分析.如 GERT，是在 1962年埃斯的广义网络计划技术基础上经过埃尔玛格拉比等人不断完善发展而来，它运用随机型解决不受限制的工作流向，按随机变量的方法对符合概率分布的工作时间进行分析和判别其时间可靠性[3].

国内相关研究方面，邓铁军教授对工程结构可靠性进行了定义，指出结构可靠性的研究重点为如何在施工期内确保工程结构达到原设计结构方案的可靠性[4].陆宁等对国内外施工项目工期、成本和质量三大目标管理进行了分析，提出以施工工序为基本组件对施工项目三大目标的可靠性进行衡量和分析[5].

综上所述，引入施工可靠性思想研究工程项目管理问题具有理论研究基础和实践应用空间，基于该视角研究工程项目管理具有一定的可行性.然而，受研究领域技术基础、管理体制等各方面条件的限制，可靠性理论和方法在不同领域的应用模式并不相同，可靠性技术、可靠性管理的应用程度和范围基本上都是结合具体行业和不同项目的特点以独自的形式发展.具体到建筑施工领域而言，其施工可靠性更具有自身的特点，需要一套与自身相适应的工程项目施工可靠性理论与方法体系.

1 工程项目施工可靠性理论体系

1.1 工程项目施工可靠性内涵界定

根据国家相关标准规定，可靠性是指产品在规定的时期内，在规定条件下，在规定的时间内完成规定功能的能力[6].工程项目这类特殊的产品，同样也可以用可靠性指标来衡量.工程项目管理是一种多目标管理，不仅仅涉及产品质量问题，它更具有多个目标形成的目标体系.H. Kerzner认为成功的项目管理可以定义为在下列条件下实现了项目目标[7]：（1）在一定的时间内；（2）在一定的费用内；（3）在要求的性能或技术水平下；（4）高效有力地运用分配的资源；（5）被顾客认可.可以理解为，前三个目标是项目管理的基本目标，第四个目标是实现前三个目标的手段，第五个目标是项目的总体和最终的目标.

借鉴可靠性理论及管理思想，并结合 Harold Kerzner对成功项目管理的描述，此处界定施工可靠性的含义如下：施工可靠性是指在工程项目施工生产过程中，在限定的工期内，在规定的成本目标范围内，能使规定的工程质量安全有效地实现的能力.这一指标在此具有特定的内涵，也即实现将实际成本控制在目标成本内的经济性，达到工期要求可信性，确保施工过程的安全性以及达到质量标准所规定的实用性，即成本经济性、工期可信性、施工安全性和质量可达性.

1.2 工程项目施工可靠性理论体系研究内容

工程项目施工可靠性理论与方法体系，属于较新的一个研究课题.该课题的研究内容大致分以下几个方面[8]：

（1）工程项目施工可靠性的概念设定；

（2）工程项目施工生产流程分解及施工网络系统构建；

（3）预测工程项目施工系统各工作单元的时间可靠性、成本可靠性、质量可靠性和安全可靠性；

(4) 根据网络系统可靠性计算的不交化最小路集原理，计算工程项目施工系统可靠性；

(5) 确定工程项目施工可靠性的评价标准；

(6) 在施工可靠性约束条件下，对工程项目多目标协同优化进行研究.

本文主要涉及（1）、（5）两个方面，也即在对各工作单元施工可靠性科学预测及整个系统施工可靠性计算完成的前提下，为工程项目施工管理水平确定评价标准，对施工系统可靠性进行评价研究，其余相关研究见文献[9-11].

2 基于模糊数学理论划分施工可靠性的评价区间

长期以来，在对工程项目管理进行评价时，项目管理者通常采用定性评价方法来衡量施工管理工作的好与坏.定性评价容易导致主观性太强，因而对工程项目管理工作有效的评估需要一个能综合反映各管理目标的量化指标和标准，引入工程项目施工可靠性这一综合指标可有效解决这个问题.文献[8-11]已经为施工可靠性的进一步研究提供了理论基础，但迫切需要建立一个“度”的衡量标准，从量化的角度出发对工程项目施工管理工作进行科学的评价.合理划分工程项目施工可靠性的评价区间，有利于对工程项目施工状况做出更具体、更科学地评价.

目前，各个学科领域定量化、数学化已是当代科技发展的趋势之一，将评价区间这些模糊概念定量化的数学方法已成为迫切需求.模糊数学理论为该问题提供了很多有价值的思想和方法.模糊数学在经济管理、科学管理、社会科学等方面被广泛应用.如，研究者经常用贫困型、温饱型、小康型、富裕型等模糊的概念对某个领域的经济发展水平进行评价，必须通过模糊数学模型方能得到符合实际的评价.同理，工程项目施工可靠性的概念也是模糊的，如可靠，较可靠，很可靠，很不可靠等，故可以采用模糊数学的方法对其进行界定和评价.

2.1 模糊语言算子与隶属函数

模糊数学是一种研究不确定性或模糊性问题的理论方法，美国著名的计算机与控制论专家扎德（L.A.Zadeh）教授于1965年提出了模糊集的概念，模糊数学从此诞生，如今模糊数学已成为一个较为完善的数学分支.运用模糊数学研究工程项目施工可靠性的评价标准，主要思路是基于模糊数学中的模糊语言变量和语气算子，确定其隶属函数，根据隶属函数运算规则合理划分评价区间.

2.1.1 模糊语言变量与语言算子

语言变量的概念是模糊数学理论中模糊逻辑与近似推理的一个基本工具，也称高阶变量.一个语言变量用一个五元组[12]（X,U,W（x）,G,M）表示.其中：X为变量名；U是论域；W（x）（简记为W）为x的术语集合，即U上x的模糊集名称的词或术语的集合， )(xWX∈ 也被称作x的语言值，是一个模糊变量；G是用于产生x的语言值的一个语法规则；M为一个语义规则.

自然语言中，一些词语如“略”、“稍许”、“很”、“比较”、“非常”等，把这些表示程度的词语缀在一个单词前面，如以“好”这一单词为主体形成“比较好”、“很好”[8]等，便改变了该词词义的肯定程度，使原来的单词变成一个新词.因此，可以分别把这些词当做一种算子，也即前述的语气算子.严格定义如下：

设 X为 论 域 ， 对 λ ∈ R+， 定 义 映 射Δ λH (λ)A→(A),(A)(x)=(A(x))，称 为语气算子；当λ＞1时，H(λ)称为集中化算子；当λ＜1时， H(λ)称为弱化算子.

设[极]= H(4)，[很]= H(2)，[相当]= H(1.25)，[比较]= H(0.75)，[有点]= H(0.5)（=[略]），[稍微有点]= H(0.25).

2.1.2 隶属函数

在模糊数学理论中，其基本思想就是隶属程度的思想.在研究中需要建立实际问题与模糊集之间的纽带，这是研究的核心，而这一纽带就是隶属函数.因此，建立符合实际的隶属函数是应用模糊数学方法的关键所在.运用模糊变量和模糊算子对工程项目施工可靠性评价标准进行划分，需要确定合理的隶属函数，这是研究的前提所在.

加强相关工作人员的责任心。档案工作目前还存在着，资料归档、整理不及时，工程施工、检查记录与工程施工不同步、资料与实际情况不相符及记录不规范的现象。我们采取了一是项目部设有专人负责工程资料的收集；二是编制了统一的表格，尽量使记录表格化，并细化相关填写标准；三是公司本部及项目部技术人员，分别经常性地组织检查，按检查结果进行奖惩等措施，努力提高管理工作水平。

2.2 工程项目施工可靠性评价区间的划分

2.2.1 运用模糊语言算子界定评价区间

对工程项目施工可靠性的评价标准进行制定时，语言变量为施工可靠性，在论域[0，1]也即可靠性取值范围内，运用模糊数学中的语气算子，可将其划分为七个基本模糊子集，分别是：很可靠A1、可靠 A2、略可靠 A3、临界可靠 A4、略不可靠A5、不可靠A6、很不可靠A7.

2.2.2 确定隶属函数

根据扎德（L.A.Zadeh）1973年提出的“真”和“假”的隶属函数[13]，“可靠”的隶属函数A2(x)

根据扎德（L.A.Zadeh）1973年提出的“真”和“假”的隶属函数[13]，“可靠”的隶属函数A2(x)为

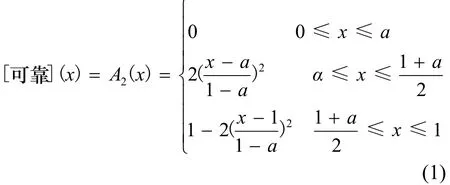
其中：x=(1+a)/2称为交叉点，]1,0[∈a是一个参数，它表示关于x的最小值的主观判断.

用 A1（x）、A2（x）…A7（x）分别表示界定的七个模糊子集的隶属函数，根据前述对模糊语气算子的定义，可得到七个模糊子集之间的隶属函数关系式为

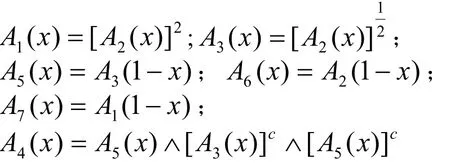
这七个基本模糊自己之间存在模糊包含关系，有

通过下列一些关系式，可根据“挖掘”的办法，推导出不具备模糊包含关系的相互独立的七个新的隶属函数：

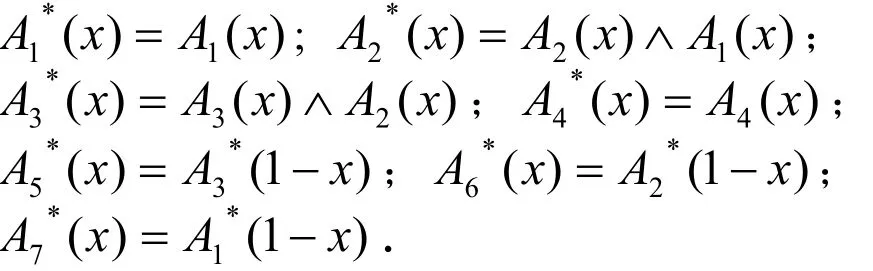
根据以上运算规则，计算出它们的隶属函数分别如下所示：

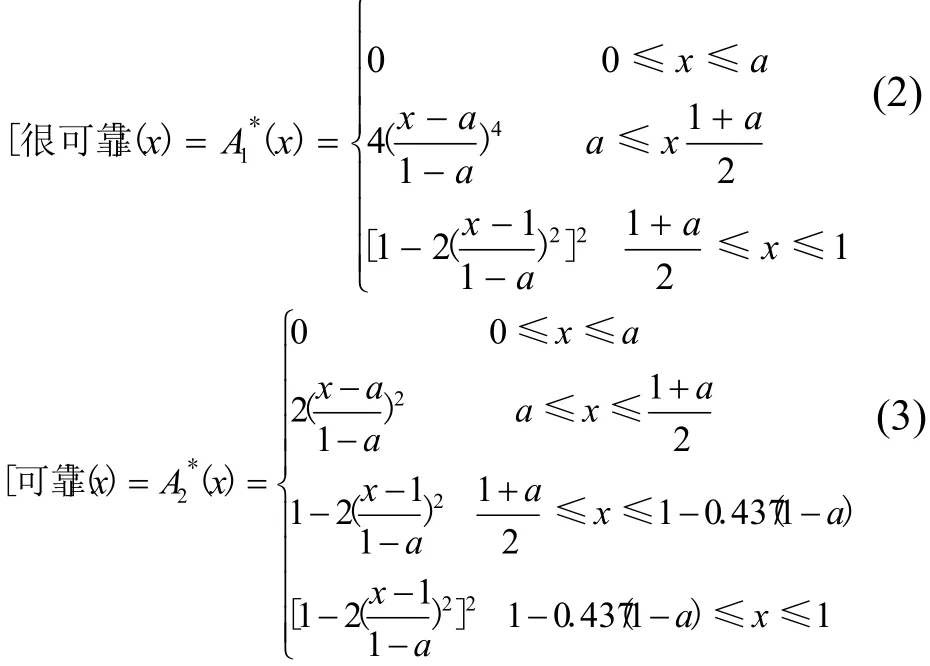
2.2.3 评价区间求解

根据以上求得的七个隶属函数，画出其曲线图，如图1所示.

由图1可看出，可靠性的取值空间[0,1]被七条曲线的六个交点分成七个互不包容的区间，由最大隶属度原则可判断出各区间对应的模糊语言值.

对各交点对应的可靠度值分别进行计算，结果为

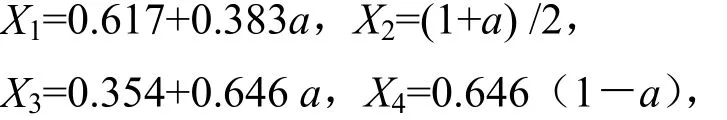
X5=0.5（1－a），X6=0.383（1－a）.

图1 隶属函数曲线及交点Fig.1 Membership function curve and intersections

则概率区间[X1，1]对应的语言值为“很可靠”，[X2，X1]对应“可靠”，[X3，X2]对应“略可靠”，[X4，X3]对应“临界可靠”，[X5，X4]对应“略不可靠”，[X6，X5]对应“不可靠”，[0，X6]对应“很不可靠”.

2.2.4 评价区间中参数a的确定

由上述分析结果可见，隶属函数中的参数a的取值直接影响评价区间的划分.a的取值因不同地域、不同类型的工程项目的判别标准不同而发生变化，由此来体现评价标准的差别性和动态性.实际应用中，应选取各地区典型工程，对其往年历史资料进行统计分析，对其隶属函数及参数a合理取值，这是对施工可靠性评价区间合理确定的关键.

假定a=0.6，则各评价区间如表1所示.

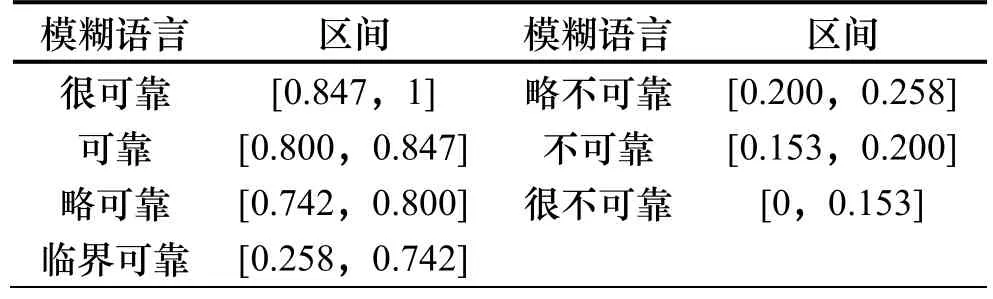
表1 工程项目施工网络系统可靠性评价区间Tab.1 Evaluation interval of construction reliability for engineering project

3 结 论

基于系统可靠性理论，将施工可靠性引入工程项目管理中，对工程项目施工可靠性及评价标准开展了探索性研究，主要取得以下几点结论：

（1）界定了工程项目施工可靠性的概念，其含义是指工程项目的工期可信性、成本经济性、质量可达性和施工安全性.

（2）基于模糊数学理论中的模糊语言算子对施工可靠性评价区间进行了合理划分.

可靠性取值空间可分为“很可靠”、“可靠”、“略可靠”、“临界可靠”、“略不可靠”、“不可靠”、“很不可靠”七个模糊子集，根据语气算子之间的运算关系得出各模糊子集的隶属函数，可靠性的取值空间[0,1]被七条函数曲线的六个交点分成七个相互独立的评价区间，由最大隶属度原则判断各区间对应的模糊语言值.由隶属函数所得的评价区间的划分受隶属函数中的参数 a的影响.a值因不同地域、不同类型的工程项目判别的不同而改变，由此来体现评价标准的差别性和动态性原则.

References

[1] AASHTO. American Association of State High Way and Transportation Officials [M]. New York: AASHTO Guide for Design of Pavement Structure,1986.

[2] C.A.乌沙茨基,刘统畏.城市建设组织计划与管理[M].北京:中国建筑工业出版社,1988.WUTZKI C A, LIU Tongwei. Urban construction plan ning and management[M]. Beijing: China Construction Industry Press, 1988.

[3] 中国建筑学会.工程网络计划技术规程教程[M].北京:中国建筑工业出版社,2000.Chinese Architectural Society . Course of network planning technique[M]. Beijing: China Construction Industry Press, 2000.

[4] 邓铁军. 结构工程施工系统可靠性理论方法及其应用的研究[D].长沙：湖南大学, 2007.DENG Tiejun. Research on theory and method of reliability in structural engineering construction system[D].Changsha: Hunan University,2007.

[5] 陆宁,廖向晖,王巍,等.大型施工项目管理可靠性综合控制的构架研究[J].重庆建筑大学学报, 2007, 29(2):132-134.LU Ning , LIAO Xianghui , WANG Wei, et al. Comprehensive control technique of reliability in large construction project management[J]. Journal of Chongqing Construction University, 2007,29(2):132-134.

[6] 梅启智, 廖炯生, 孙惠中. 系统可靠性工程基础[M].北京: 科学出版社, 1992.MEI Qizhi, LIAO Jiongsheng, SUN Huizhong. Engi neering foundation of system reliability[M]. Beijing:China Science Press, 1992.

[7] KERNER H. Project management: A systems approach to planning, scheduling and controlling[M].New York:John Wiley&Son,Inc.Press,2006.

[8] 史玉芳.建筑工程项目施工网络系统可靠性测定、评判与优化研究[D].西安：西安建筑科技大学，2011.SHI Yufang. Studies on construction network reliability determination, evaluation and optimization of engineering project[D].Xi’an: Xi’an Univ. of Arch. & Tech,2011.

[9] 史玉芳，解燕平，陆路. 矿业工程项目施工工期可靠性预测研究[J].西安科技大学学报:自然科学版，2011,31(5)：593-597.SHI Yufang, XIE Yanping, LU Lu. Construction time reliability forecasting of mining project[J]. J.Xi’an Univ. of Sci. & Tech.: Natural Science Edition, 2011,31(5)：593-597.

[10] 史玉芳，李慧民，陆宁.工程项目施工系统可靠性及计算方法研究[J].西安建筑科技大学学报:自然科学版，2011,43(1)：125-130.SHI Yufang, LI Huimin, LU Ning. Research on construction system reliability of engineering project and its calculation method[J]. J.Xi’an Univ. of Arch. & Tech.:Natural Science Edition, 2011,43(1):125-130.

[11] 史玉芳，李慧民，陆宁. 基于遗传算法的公路施工项目成本优化研究[J].建筑经济，2009,(7):66-70.SHI Yufang, LI Huimin, LU Ning. Study on project construction cost optimization based on Genetic Algorithm[J]. Architecture economy, 2009,(7):66-70.

[12] 彭祖赠, 孙韫玉. 模糊数学(Fuzzy)及其应用[M]2nd ed.武汉：武汉大学出版社, 2007.PENG Zuzeng, SUN Wenyu. Fuzzy and application [M]2nd ed. Wuhan: Wuhan University Press, 2007.

[13] 梁保松, 曹殿立. 模糊数学及其应用[M].北京：科学出版社,2007.LIANG Baosong, CAO Dian-li. Fuzzy and application[M]. Beijing: Science Press, 2007.