结构抗连续倒塌鲁棒性简化分析方法研究
杜永峰,包 超,宋 翔,张尚荣,谢 丽
(1. 兰州理工大学西部土木工程防灾减灾教育部工程研究中心,甘肃 兰州730050;2. 兰州理工大学防震减灾研究所,甘肃 兰州730050)
随着诸如英国伦敦 Ronan Point公寓,美国Alfred P. Murrah政府大楼,以及美国世贸大厦等一系列建筑连续倒塌事件的发生,如何增强建筑结构的鲁棒性(structural robustness)也成为全世界土木工程界探讨的热点问题.结构的鲁棒性是指建筑结构承受局部损伤并抵抗不相称破坏的能力[1].
为了保证建筑结构在极端条件下也能够具备一定的鲁棒性,国际上已有多个国家先后推出了相关的标准和规范.1994年英国结构安全标准委员会(SCOSS)将结构鲁棒性和易损性提升至与结构安全储备、设计和施工过程安全监督检查同等重要的地位,并将其看成是确保结构安全不可忽视的三个重要措施之一[2].国际结构安全联合委员会(JCSS)于2008年颁布“工程风险评估原理”指南[3],并将工程结构的鲁棒性纳入到整个风险评估框架之中,指出工程的风险评估包括危险性、易损性和鲁棒性三个基本组成部分,并给出了鲁棒性的定量指标和分析方法.2006年美国土木工程师学会(ASCE)在标准 ASCE 7-05[4]中要求结构应能够承受局部损伤,同时其整体保持稳定而不致造成与初始损伤不相称的破坏.
针对建筑结构鲁棒性问题,国内外学者已经做了大量深入研究.高扬和刘西拉[5]对结构鲁棒性评价中的构件重要性系数进行研究,以移除所分析构件前后的结构承载力变化为着眼点,给出一个结构鲁棒性评价中计算构件的重要性系数的新方法;吕大刚等[6]分别采用基于承载力、可靠度以及风险鲁棒性指标,对钢筋混凝土框架结构的抗震鲁棒性进行了定量评价;Starossek等人[7]分别基于损伤、能量和刚度矩阵提出了三个指标对鲁棒性进行定量分析;黄靓等[8]基于改进的构件重要性系数提出了一种新的结构鲁棒性指标,并实现了结构鲁棒性的量化;Maes[9]提出以完好结构承载力与损伤结构承载力的比值作为结构鲁棒性的评价指标;张卫喜等[10]基于拆除构件法,从理论上推导动力放大系数与失效时间的关系,得出框架柱失效过程中失效点处初始位移、最大静位移和最大动位移变化特点,以及动力放大系数随失效时间和失效位置的变化规律;郑山锁,田进等[11]分别将增量动力分析方法和静力非线性方法与蒙特卡洛抽样相结合,从而得到结构概率地震需求及概率抗震能力的统计,并提出了地震易损性模型;李晓文等[12]从力学机制和抗力分布规律出发,提出了基于塑性铰线理论的板柱结构抗连续倒塌设计方法.
已有的研究成果大多关于水平作用下结构的鲁棒性,结构水平向连续倒塌只是结构倒塌形态中的一种[13],对该倒塌模式结构鲁棒性的研究成果无法完全适用于其余倒塌模式,为此本文对意外荷载作用下结构抗竖向连续倒塌的鲁棒性进行研究,针对性地改进了构件易损性系数的计算方法,并对一钢筋混凝土框架结构的抗竖向连续倒塌鲁棒性进行评价和分析.
1 结构抗连续倒塌鲁棒性计算
1.1 构件易损性系数
现有研究主要围绕结构的易损性展开的,即整个结构在极端事件中可能受到伤害或造成损伤的程度,如果很小的初始破坏造成了不成比例的严重破坏后果,那么这个结构就是易损的.结构易损性不仅取决于结构的布置形式,建筑材料的性能,还与关键构件的设计和构造措施等有关.
相比于结构易损性,构件易损性主要针对于构件在外部荷载作用下发生破坏的概率.对于单个构件来说,如果某一荷载所引起的荷载效应远远小于构件抗力,则该构件在此荷载作用下损伤风险就相对较低,构件易损性系数也较小,反之,此荷载增大时该构件被破坏的风险则较大,所对应的易损性系数就较大.
黄靓等[14]基于构件承载力建立了多种相关荷载作用下构件易损性系数,从而能够定量地评价构件易损程度,但是该方法用于构件数目较多的复杂结构时,计算量将变得异常庞大.针对结构抗竖向连续倒塌鲁棒性展开研究,考虑的主要外部荷载为结构所受竖向荷载;由荷载传递路径可知,上部竖向荷载均由框架柱承担,而框架柱的失效与否直接关系着整体框架结构是否发生竖向连续倒塌.所以选取框架柱所受轴力作为构件易损性系数的评价指标,故在文献[14]基础上做了更进一步的简化.

式中:φi为构件i轴向荷载作用下的易损性系数;Ni和 Ni0分别为构件i的正截面所受轴力和正截面承载力.
由于
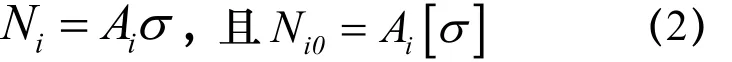
可有

式中:σ为构件i正截面压应力;[]σ为材料容许压应力.
由式(3)可知,0≤φi≤1,当φi=0时,表示构件i在该特定外部荷载作用下未分配到荷载,在该外部作用中没有提供任何抗力,易损性也就为零.当φi=1,则表示构件i在承受该特定荷载的过程中达到了其设计承载力,若荷载继续增大则该构件将受损失效.
1.2 构件重要性系数
评估构件重要性是研究结构鲁棒性的基础[15],通常采用构件重要性系数来衡量构件的重要程度.构件重要性系数用于反映结构在极端条件下个别构件破坏对整体结构性能的影响程度.高扬[16]综合考虑了结构的几何拓扑关系、构件的刚度和强度以及外荷载的影响,提出基于结构承载力系数的构件重要性系数,但在其所提公式中以结构承载力设计基准值为比较对象,物理意义不够清晰.为此,黄靓等[8]在文献[16]的基础上对其从形式上加以改进,计算公式表示:

式中:iγ为构件重要性系数;0R和iR分别为原结构极限承载力和构件i失效后剩余结构的极限承载力.
改进后的公式形式更加简洁明了,物理意义也更加明确了.基于文献[8]改进后的构件重要性系数对目标构件进行重要性评价.
1.3 结构鲁棒性系数
构件易损性系数反映了构件的易损程度,而构件重要性系数用于反映某构件失效可能引起的结构破坏程度,这两个概念从不同的侧重点表现了构件与结构之间的相互联系,将二者综合起来才能对结构的鲁棒性作出全面评价.
正是基于该思想提出了综合考虑了构件易损性系数和构件重要性系数的结构鲁棒性系数,但该鲁棒性系数对式中各变量的变化过于敏感[16],而区分度又不明显,所以本文对其表达式从形式上做了一定改进,即:

式中:R为结构鲁棒性系数;iφ和iγ分别为第i构件的构件易损性系数和重要性系数.结合上式分析可知,构件易损性系数和重要性系数越小,结构鲁棒性系数就越大,结构抗竖向连续倒塌的鲁棒性越好.这一点也符合工程中的实际情况:当结构中各构件的易损性系数较小,即构件不易被破坏,且相应构件的重要性系数也较小,即该构件的损伤对整个结构承载力影响又不大,那么整体结构抵御该特定荷载作用的能力就会增大.
2 分析模型
利用有限元软件SeismoStruct[17]建立一栋6层5跨钢筋混凝土框架结构并以此作为研究对象,梁和柱均采用 C30级混凝土,构件纵向钢筋采用HRB335级;柱距6 m,各层层高3.3 m;柱截面尺寸600 mm×600 mm,梁尺寸300 mm×600 mm,结构平面布置如图1所示.
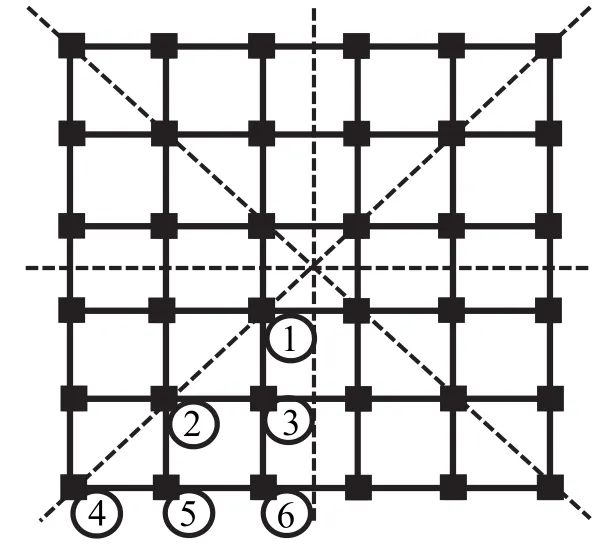
图1 结构平面布置图Fig.1 Plan-view of RC frame
由于本模型为平面双向对称模型,为避免重复运算并提高运算效率,将原结构用四条对称轴划分为8份结构参数相同的部分作为研究对象.将研究对象中的6根假设失效的底层框架柱分别对应6个不同工况.
3 分析方法和步骤
研究框架结构抗连续倒塌的鲁棒性,主要考虑框架柱所受轴向作用,所以针对框架柱轴向荷载及剩余结构的竖向位移展开分析.在确定构件易损性系数时,为了考察构件在不同大小的荷载条件下,构件易损性及其对鲁棒性的影响特征,选取了多个不同大小的荷载进行分析.在对构件重要性系数进行计算时,引入 Pushdown方法[18-19]来确定原结构和剩余结构的极限承载力.
进行结构 Pushdown分析时,对结构顶部各节点施加竖直向下的推覆力,而推覆力可以表示为推覆力增量步乘以荷载系数(Load factor)的形式,各工况中结构对应的极限承载力也可如此表示.荷载系数在零到目标值的区间内逐渐递增搜索,该目标值也就是推覆分析中提前设定的控制目标,当达到控制目标或结构在达到控制目标前倒塌,分析随即终止,此时推覆力增量步的放大倍数就是荷载系数.具体步骤如下:
首先,选取数个确定的荷载值并施加于结构上,根据各构件内力和极限承载力确定其相应的易损性系数iφ.
其次,对完成的无损伤的原结构进行Pushdown方法分析,确定原结构竖向极限承载力;然后依次拆除研究对象中底层各框架柱,并再次利用Pushdown方法对相应模型进行分析,确定各种不同工况所对应的剩余结构极限承载力;利用等式(4)计算各底层框架柱的重要性系数.需要补充的是,为了保证计算结果的准确性,整个分析过程中推覆力增量步取值较小为1 kN并保持不变,从而结构的极限承载力可以被简化为荷载系数来表示.
最后,将计算所得的构件易损性系数和构件重要性系数代入等式(5)从而确定相应工况中剩余结构抗竖向连续倒塌鲁棒性.
4 计算结果及分析
4.1 构件易损性系数
对结构各层楼板分别施加3 kN/m2,6 kN/m2,9 kN/m2,12 kN/m2和15 kN/m2共5个不同等级的竖向均布荷载,并依次记做L1,L2,L3,L4和L5.根据不同等级中分布荷载大小和框架柱分配承载面积的大小计算可得各底层框架柱轴力,见表 1.结构底层框架柱截面尺寸和所用材料均相同,因此各构件具有同样的极限承载力,由构件尺寸和材料强度可求得其所能承载的最大轴向压力为10.8×103kN.求得底层框架柱极限承载力后,根据表1中各构件轴力大小即可确定相应构件的易损性系数.
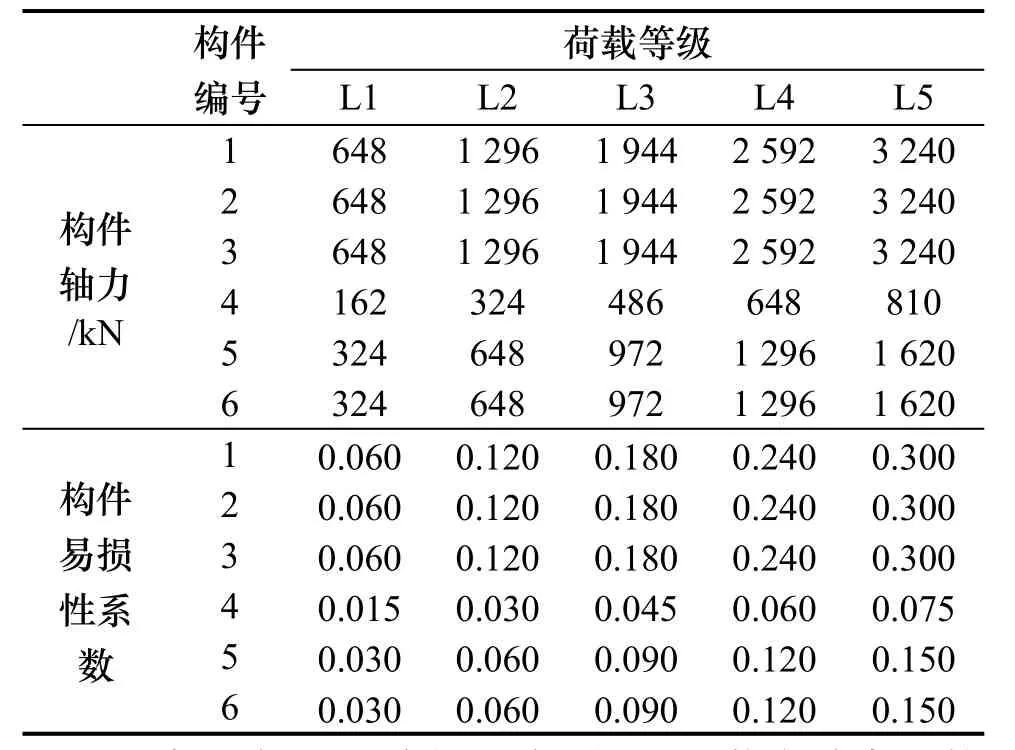
表1 构件易损性系数Tab.1 Member vulnerability coefficients
从表1中可以看出,对于极限承载力确定的构件,易损性系数随着所受外部荷载的不同而不同,且构件易损性系数与构件内力大小呈正相关关系,即构件易损性系数随着相应构件内力的增大而增大.这一特点有着清晰的物理意义:当内力增大时,构件被破坏的风险也会增大;而当内力较小的构件显然不容易发生破坏的情况.此外,构件易损性不仅与其内力有关,还取决于构件自身的极限承载力:在相同的外部荷载作用下,具有更高极限承载力的构件就会比极限承载力较低的构件更为安全.
4.2 构件重要性系数
对原结构和全部工况中剩余结构进行Pushdown分析,利用所得荷载系数求得各个工况中所拆除构件的重要性系数,见表2.

表2 构件重要性系数Tab.2 Member importance coefficients
构件重要性系数反映了某个构件失效对整个结构承载力的影响程度,从表2可以看出,工况4所对应框架柱的重要性系数相对较大,工况5和工况6次之,工况1、工况2和工况3最小.
结合结构的平面布置图可以得到构件重要性系数存在大小差别的原因[16],工况 4所对应的框架柱为角柱,当该构件失效后,与之相连接的框架梁仅能通过梁机制来分散和传递上部荷载,无法提供承载力更大的悬链线机制来承受外部荷载和抑制剩余结构变形的发展,该构件一旦失效就会造成结构承载力出现较大的损失,因此该构件也相对更为重要;工况5和工况6所对应的边柱失效后,该框架柱所在跨内各框架梁除了提供梁机制外,还能通过单向悬链线机制继续承载,因此该构件失效对结构承载力的影响相对较小,重要程度也随之有所减小;相比工况5和工况6,与工况1、工况2和工况3中的失效中柱相连接的各框架梁可以提供双向悬链线机制来承受荷载,结构承载力损失也最少,其重要程度也就最低.
此外,同样以中柱作为失效框架柱的三个工况对应的构件重要性系数中,构件重要性系数从大到小依次对应工况2、工况3和工况1,从图1可以看出,上述3种工况对应的框架柱依次接近结构平面几何形心,这主要因为框架柱越靠近结构平面几何形心,则在其失效后剩余结构约束侧向变形发展的能力越强,剩余结构竖向变形发展也会越困难且更加不容易倒塌失效,构件重要性系数也随之减小.与之类似,工况5对应的构件重要性系数略大于工况 6.由以上分析可知,靠近结构平面几何形心的构件其重要性系数相对较小,该构件失效对结构极限承载力造成的影响较小.
4.3 结构鲁棒性系数
由于仅针对原结构中1/8部分的底层框架柱轴向荷载进行了分析,因此所计算的结构鲁棒性是指底层框架柱失效时抵抗竖向连续倒塌能力,不同等级的竖向荷载作用下结构抗竖向连续倒塌的鲁棒性系数如图2所示.

图2 结构鲁棒性系数与荷载等级关系曲线Fig.2 Contrast between structural robustness and loadings
从图中可以看出,结构鲁棒性系数随着竖向荷载的增大而表现出减小趋势,即结构的抗竖向连续倒塌的鲁棒性随着竖向荷载的增大而变差,表明结构鲁棒性的优劣是一个相对概念.对于研究的荷载形式确定的结构,各工况所设定的初始失效框架柱在该荷载作用下的构件重要性系数也是确定值,在此特定条件下,结构鲁棒性系数就只取决于构件的易损性系数,而由式(3)可知,构件易损性系数高低与其内力大小呈正相关的关系,从而结构鲁棒性系数与所分析构件的易损性系数呈反相关的关系.
从以上分析可以看出,对于外部荷载确定的结构,结构中各构件内力也是确定的,提高重要构件的极限承载力或增设防护设施以降低其易损性风险;而如果对重要构件合理地设置“替补”构件,则能够降低该构件的重要程度,通过降低重要构件的重要性程度及其易损性风险就能够实现提高结构鲁棒性的目的.
5 结论
(1)结构鲁棒性的优劣是一个相对概念,取决于构件易损性和构件重要性.对于指定的荷载作用形式,构件重要性系数就能够被确定;荷载作用形式和大小均被指定,则构件的易损性系数也就得以确定.
(2)在同样荷载作用下,中柱重要性系数最小,边柱次之,角柱最大;与之相反,中柱易损风险最大,其次是边柱和角柱.增加备用荷载路径能够减轻个别构件失效对结构承载力造成的不利影响,并降低该失效构件的重要程度;在易损构件附近增设与之相似承载构件,可以分担易损构件所受荷载并降低其损伤风险.
(3)控制外部荷载作用形式,避开或减小对结构最为不利的荷载,可以降低某些构件重要性系数,减轻引起失效对结构造成的不利影响;降低荷载大小,则能够降低构件损伤风险,增强结构鲁棒性.
结构抗竖向连续倒塌鲁棒性是一个相对概念,能够对多种不同建筑造型和荷载布置的结构进行分析和评价,并从中确定鲁棒性相对优劣情况,然而,对于某个单一研究对象,利用本方法可以得到对应该结构特征的一个具体的鲁棒性系数,由于缺乏确定的参考标准而难以对其鲁棒性的优劣进行评价.在后续研究中还需要对该鲁棒性做进一步的深入研究,提出该鲁棒性评价的参考标准,使其可以被应用于更多结构的抗竖向连续倒塌鲁棒性评价中.
References
[1] ELLINGWOOD B R. Mitigating risk from abnormal loadsand progressive collapse[J]. Journal of Performance of Constructed Facilities, 2006, 20(4): 315- 323.
[2] The Standing Committee on Structural Safety (SCOSS).10th Report of SCOSS[R]. London: SETO Ltd, 1994.
[3] FABER M H. Principles of risk assessment in engineering[R]. Zurich: Joint Committee of Structural Safety Publication, 2008.
[4] ASCE 7-10. Minimum design loads for buildings and other structures[R]. New York: American Society of Civil Engineers, 2006.
[5] 高扬, 刘西拉. 结构鲁棒性评价中的构件重要性系数[J]. 岩石力学与工程学报, 2008, 27(12): 2575-2584.GAO Yang, LIU Xila. Importance coefficients of components in evaluation of structure robustness[J].Chinese Journal of Rock Mechanics and Engineering,2008, 27(12): 2575-2584.
[6] 吕大刚, 宋鹏彦, 崔双双, 等. 结构鲁棒性及其评价指标[J]. 建筑结构学报2011, 32(11): 44-54.LU Dagang, SONG Pengyan, CUI Shuangshuang, et al.Structural robustness and its assessment indicators[J].Journal of Building Structures, 2011, 32(11): 44-54.
[7] STAROSSEK U,HABERLAND M.Evaluating measures of structural robustness [C]. Structures Congress, ASCE,2009: 1758-1765.
[8] 黄靓, 李龙. 一种结构鲁棒性量化方法 [J]. 工程力学,2012, 29(8): 213-219.HUANG Liang, LI Long. A quantification method of structural robustness[J]. Engineering Mechanics, 2012,29(8): 213-219.
[9] MAES M A, FRITZSONS K E, GLOWIENKA S.Structural robustness in the light of risk and consequence analysis[J]. Structural Engineering International, 2006,16(2): 101-107.
[10] 张卫喜, 屠冰冰, 赵冬. 连续倒塌过程中构件失效动力效应分析[J]. 西安建筑科技大学学报: 自然科学版,2014, 46(1):84-89.ZHANG Weixi, TU Bingbing, ZHAO Dong. Analysis on dynamic effect of component failure during progressive collapse[J]. Journal of Xi'an Univ. of Arch. & Tech.:Natural Sciences Edition, 2014, 46(1):84-89.
[11] 郑山锁, 田进, 韩言召, 等. 考虑锈蚀的钢结构地震易损性分析[J]. 地震工程学报, 2014, 36(1): 1-6.ZHENG Shansuo, TIAN Jin, HAN Yanzhao, et al.Seismic fragility analysis of steel structure considering steel corrosion[J]. China Earthquake Engineering Journal,2014, 36(1): 1-6.
[12] 李晓文, 古腾达, 李健勋. 基于能量法的板柱结构抗连续倒塌设计[J]. 低温建筑技术, 2013, 35(9): 48-50.LI Xiaowen, GU Tengda, LI Jianxun. Analysis of PC resistance performance of RC structures based on the energy principle[J]. Journal of Low Temperature Architecture Technology, 2013, 35(9): 48-50.
[13] 崔双双. RC框架结构整体抗震性能系数与综合反应修正系数研究[D]. 哈尔滨: 哈尔滨工业大学, 2013.CUI Shuangshuang. Research on global seismic prehensive response modification factors of RC frames structures[D]. Ha’erbin: Harbin Institute of Technology,2013.
[14] 黄靓, 王蓥, 陈永亮, 等. 一种简化的结构鲁棒性量化方法[J]. 工程力学, 2013, 30(10): 46-53.HUANG Liang, WANG Ying, CHEN Yongliang, et al. A quantification method of structural robustness[J].Engineering Mechanics, 2013, 30(10): 46-53.
[15] 蔡建国, 王蜂岚, 韩运龙, 等. 大跨空间结构重要构件评估实用方法[J]. 湖南大学学报: 自然科学版, 2011,38(3): 7-11.CAI Jianguo, WANG Fenglan, HAN Yunlong, et al.Practical method for the evaluation of important structural components of long-span space structures[J].Journal of Hunan University: Natural Sciences Edition,2011, 38(3): 7-11.
[16] 高扬. 结构鲁棒性定量计算中的构件重要性系数[D].上海: 上海交通大学, 2009.GAO Yang. Importance coefficients of components in quantitative evaluation of structural robustness[D].Shanghai: Shanghai Jiao Tong University, 2009.
[17] SeismoStruct V6.5. SeismoStruct-A computer program for static and dynamic nonlinear analysis of framed tructures [OL]. SeismoSoft ,Ltd. http:// www. Seis mosoft.com, 2012.
[18] 李易, 陆新征, 叶列平, 等. 基于Pushdown分析的RC框架抗连续倒塌承载力研究[J]. 沈阳建筑大学学报:自然科学版, 2011, 27(1):10-18.LI Yi, LU Xinzheng, YE Lieping, et al. Study on progressive-collapse resistance capacity of RC frame structures based on pushdown analysis[J]. Journal of Shenyang Jianzhu University: Natural Sciences Edition,2011, 27(1):10-18.
[19] KHANDELWAL K, El-Tawil S. Pushdown resistance as a measure of robustness in progressive collapse analysis [J]. Engineering Structures, 2011, 33(9):2653-2661.

