RC伸臂梁钢纤维砂浆钢筋网抗剪加固带性能研究

卜良桃，刘裔彬

(湖南大学土木工程学院，湖南 长沙 410082)

据统计，我国大约有三分之一的住宅安全储备不足，由于部分建筑结构老龄化、生产规模及工艺更新、抗震设防标准提高、老建筑的保护利用等，需要加固补强的结构越来越多．混凝土结构传统的加固方法很多，主要有加大截面法、增补钢筋法、体外预应力法、改变传力途径法、改变受力体系法、粘钢法、包钢法、粘贴碳纤维法等[1]．这些方法虽然有它们的适用性，但缺陷和不足也很突出．

RC梁钢纤维砂浆钢筋网抗剪加固带施工工艺简单方便．只需先对混凝土表面进行凿毛处理，然后对表面进行清洗，涂抹界面剂，再在RC梁表面每隔一定间距植入剪切销钉，铺设钢筋网，最后粉抹或喷射钢纤维水鸟砂浆即可．钢纤维砂浆和混凝土材性相近，钢纤维砂浆钢筋网薄层能和原构件协同工作．与传统加固方法相比，基本不增加构件几何尺寸和重量，试用性较强，易于推广．

目前，对RC梁钢纤维砂浆钢筋网抗剪加固带的抗剪性能研究较少，理论分析模型主要为传统的桁架—拱模型[2]．为此，本文在借鉴和总结国内外相关课题研究成果的基础上[3-6]通过RC伸臂梁钢纤维砂浆钢筋网抗剪加固带剪切破坏试验，采用塑性分析方法，提出RC伸臂梁钢纤维砂浆钢筋网抗剪加固带抗剪极限承载力计算公式，具有一定的理论意义．

1 试验方案

1.1 试验梁设计

本次试验共制作4根RC梁，试件截面设计尺寸为b×h=150 mm×300 mm ，构件长度取为L=3 200 mm，试验梁设计参数见表1、试验梁材料参数见表2．原梁混凝土强度等级为 C30，加固层厚度为 25 mm，加固砂浆采用M40的钢纤维砂浆，由p.o.42.5普通硅酸盐水泥、中砂、钢纤维和水组成，配合比为水泥：砂：水为 1：1.9：0.45，钢纤维参量体积分数为2%．试件分为两组，第一组（B1、B2）的剪跨长度为650 mm，第二组（B3、B4）的剪跨长度为 750 mm，抗剪加固带采用通长四面环包．具体见图1．

表1 试验梁设计参数Tab.1 Designing detail of test beam

图1 试验梁受力简图、原梁及加固梁配筋示意图Fig.1 Details of test-beams

表2 试验梁材料参数参数Tab.2 Detail of material

1.2 加载方案与测试内容

试验梁通过放大系数为5.2的杠杆加载，在吊篮中按顺序堆放有质量标记混凝土试块,加载装置见图 2．参照《混凝土结构试验方法标准》[7]，首先对试验梁进行预加载，预加载值不大于理论开裂荷载计算值的70%，本试验取30 kN；试验梁采用分级加载，每级按短期试验荷载值的 10%进行加载；当加载到理论开裂荷载计算值的90%时，以后每级按短期试验荷载值的 5%加载；每级加载持荷时间为15 min，待各仪器数值稳定后读数．试验使用裂缝宽度仪测量裂缝在各荷载下的宽度，使用百分表测量集中荷载作用点、支座处挠度，运用电阻应变仪和应变片测量混凝土、砂浆、箍筋、环包钢筋网应变值，箍筋应变测试部位如图3所示．

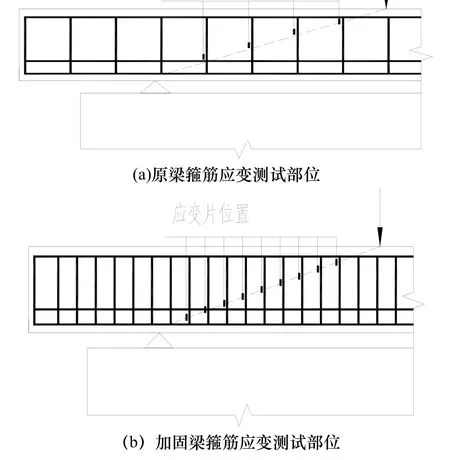
图3 箍筋应变测试部位Fig.3 Stirrup strain test site

2 试验结果与分析

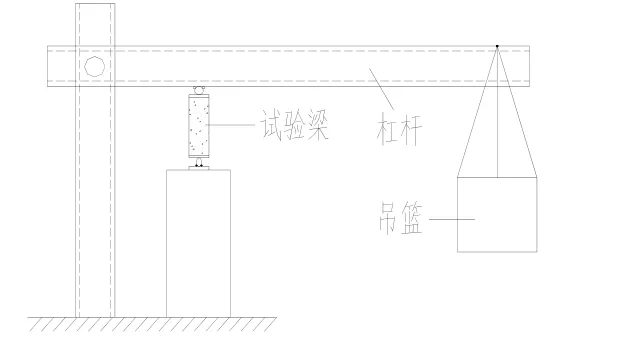
图2 加载装置Fig.2 Loading device

2.1 试验结果

本次试验所有试验梁均发生斜截面剪切破坏，试验结果如表3所示．试验结果表明，加固梁的开裂荷载和极限荷载均有一定程度的提高，加固梁受剪极限荷载提高幅度大于开裂荷载提高幅度， 加固梁剪跨比变化，加固梁受剪极限荷载值相近．

表3 试验结果Tab.3 Experimentational Results

2.2 典型破坏形态

原梁和加固梁均呈现典型剪压破坏形态．试验梁最先在弯矩较大的区段出现竖向裂缝，随着荷载的增加，裂缝斜向延伸，裂缝倾角减小．在剪跨段某截面腹部出现腹剪型裂缝，腹剪裂缝由中部沿集中荷载作用点和支座处双向延伸，离集中荷载作用点越近，裂缝越平缓，形成一条临界斜裂缝，见图4．临界斜裂缝形成后，荷载作用点附近的混凝土受压区出现水平状混凝土受压裂缝，随着临界斜裂缝宽度增加和受压区缩小，受压区混凝土被压碎．试验梁伸臂段出现反向斜裂缝，最终破坏发生在简支段．

图4 临界斜裂缝Fig.4 Critical diagonal crack

2.3 裂缝分析

在试验过程中，描绘了对比梁和加固梁裂缝宽度变化规律，试验结果见图 5．试验结果表明，对比梁斜裂缝出现后，开展迅速，斜裂缝宽度和间距较大，相反，加固梁裂缝开展缓慢，斜裂缝宽度和间距较小．在相同的荷载作用下，加固梁裂缝宽度小于对比梁．加载到原梁箍筋和加固箍筋屈服后，斜裂缝发展速度加大．试验梁破坏时，加固梁裂缝数量细而密，少量钢纤维被拔出．试验结果表明，钢纤维沙浆钢筋网能有效地延缓构件开裂，限制裂缝发展，增加构件抗裂性．

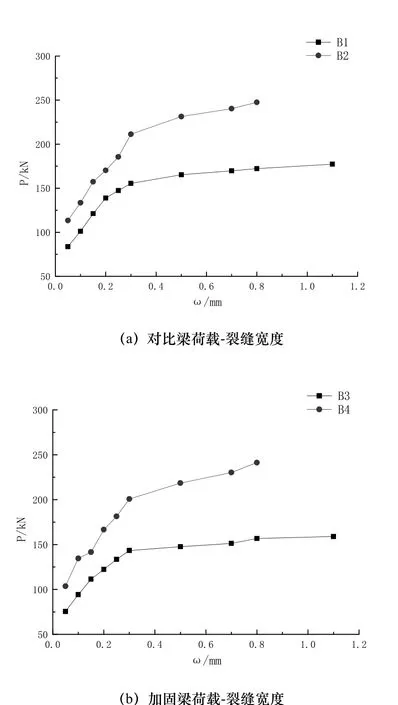
图5 荷载-裂缝宽度曲线Fig.5 Load-crack width curves of beams

2.4 挠度分析

在试验过程中，记录并描绘了试验梁的荷载—挠度曲线，试验结果见图6．试验结果表明，对比梁挠度变化较快，挠度相同时，每组对比梁荷载均小于加固梁，破坏时，加固梁挠度小于对比梁，说明钢纤维砂浆钢筋网使构件刚度增加．由试验结果分析，加固梁开裂前，钢纤维砂浆钢筋网薄层与原梁工作协同，砂浆层使构件截面尺寸增大，从而增加了构件抗弯刚度．加固梁开裂后，裂缝削弱截面抗弯刚度，而钢纤维砂浆钢筋网能有效限制斜裂缝发展，使加固梁抗弯刚度削弱程度小于对比梁，所以加固梁抗弯刚度较对比梁大．

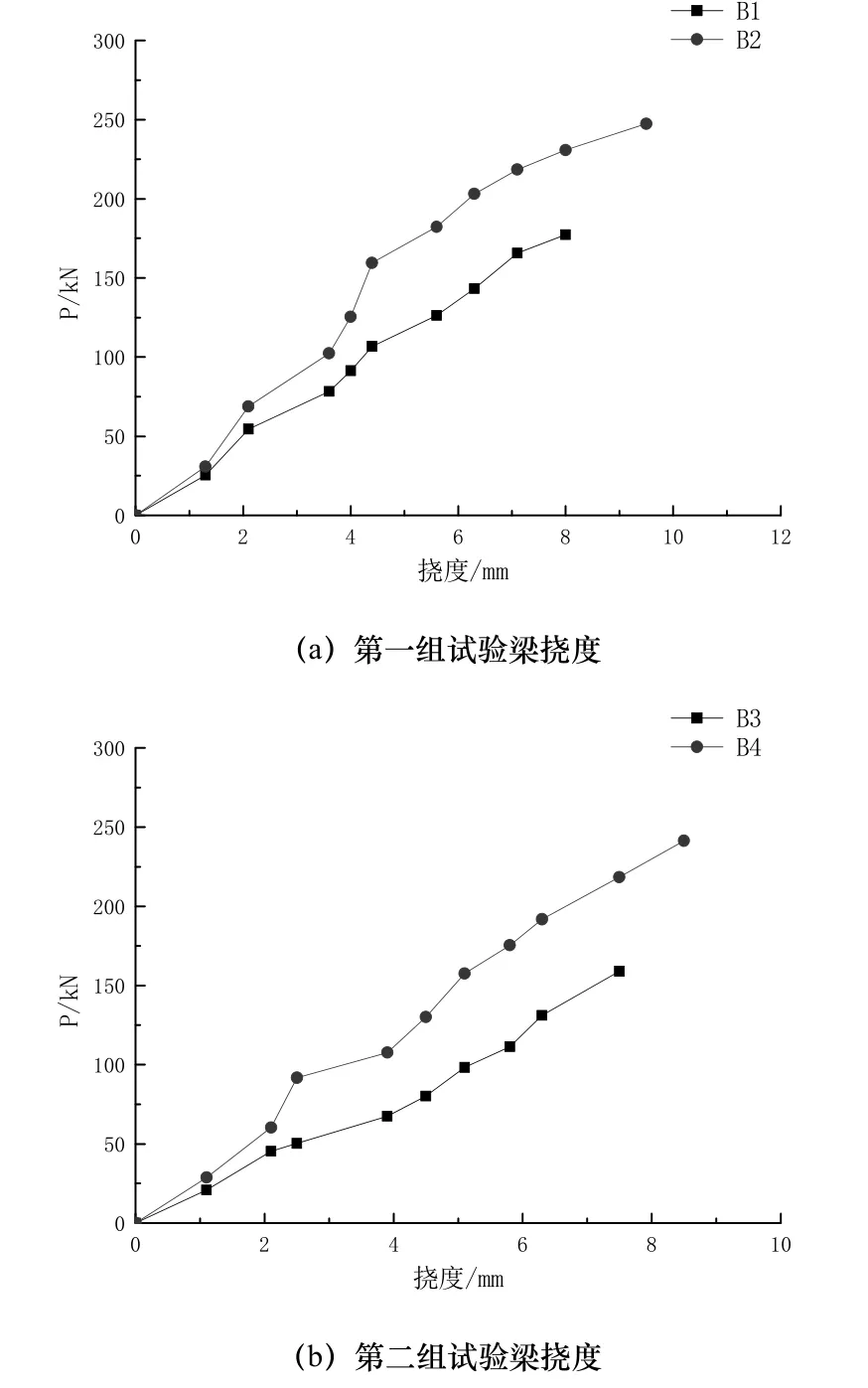
图6 荷载-挠度曲线Fig.6 Load-Deflection Curves of Beams

2.5 应变分析

根据试验过程中测得的对比梁和加固梁箍筋应变数据，描绘对比梁和加固梁箍筋荷载—应变曲线，应变取值为每根箍筋所测应变平均值，试验结果如图7所示．试验结果表明，试验梁开裂后，箍筋应变显著增大，主要因为试验梁开裂后，混凝土和砂浆层退出工作，箍筋受荷贡献突增，从而箍筋应变显著增加．在相同荷载作用下，每组加固梁箍筋应变均小于对比梁，这是因为钢纤维砂浆钢筋网薄层中横向箍筋承担了一部分荷载，使加固梁箍筋应力减小，即加固梁箍筋应变较对比梁箍筋应变小．对比梁箍筋屈服后，构件将很快破坏，加固梁箍筋屈服后，由于钢纤维砂浆钢筋网薄层中横向箍筋还未屈服，能够继续承担荷载，延性增加，所以破坏时加固层箍筋应变更大，加固梁原箍筋与加固层箍筋应变步调基本一致，说明加固层与原构件能协同工作、整体受力．

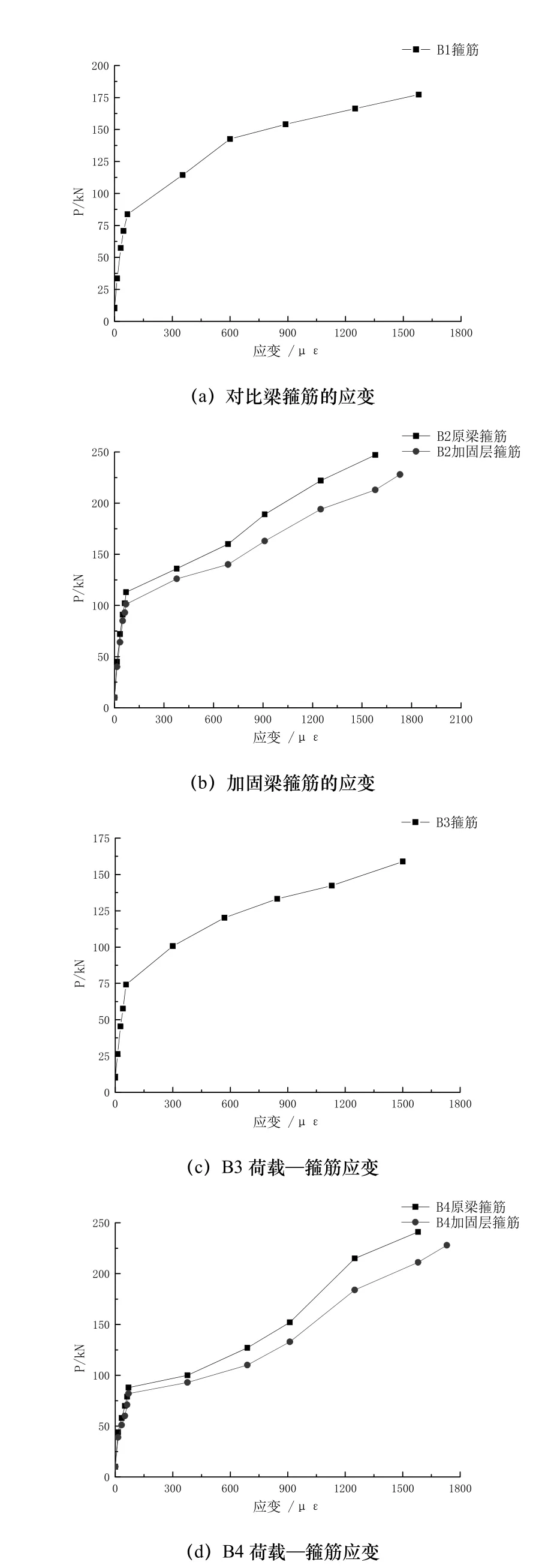
图7 荷载-箍筋应变曲线Fig.7 Load-Stirrup Strain Curves of Beams

3 抗剪加固带受剪极限承载力计算

本文根据混凝土和钢筋的本构关系及试验梁的试验结果，采用塑性分析方法，提出RC伸臂梁钢纤维砂浆钢筋网抗剪加固带斜截面抗剪强度计算公式．

3.1 基本假定

假设混凝土、钢纤维砂浆、钢筋为完全刚塑性材料[8]，钢筋只承受轴向拉应力，忽略混凝土和钢纤维砂浆的拉应力，由于钢纤维砂浆与混凝土协同变形，受压变形模量相近，可将钢纤维砂浆和混凝土视作同种材料，共同受压．钢筋单轴受拉，屈服条件为

由修正的莫尔—库伦准则，并考虑混凝土的塑性软化现象，处于平面应力状态下的混凝土和钢纤维砂浆的屈服条件为：

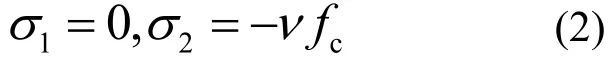
式中：sσ为钢筋应力，yf为钢筋的屈服强度，1σ、2σ为平面应力下混凝土与钢纤维砂浆主应力，cf为混凝土轴心抗压强度，ν为混凝土塑性软化系数，此处采用Nielsen经验系数[9]，取

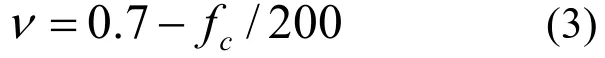
3.2 理论推导

根据塑性分析原理，抗剪加固带选用如图8所示塑性破坏机构，屈服截面将梁分为Ⅰ、Ⅱ两部分刚体，Ⅰ部分刚体仅发生相对转动，相对转角为θ，Ⅱ部分刚体仅发生相对竖直向下位移ω，屈服截面宽度值对计算结果未有影响，可取单位宽度，屈服截面与水平轴线夹角为α．利用虚功原理可求出塑性上限解，由于塑性下限解求解复杂，此处仅将上限解作为计算结果．图8中mb、mh分别为加固带截面宽度和截面高度，l为塑性铰线长度．

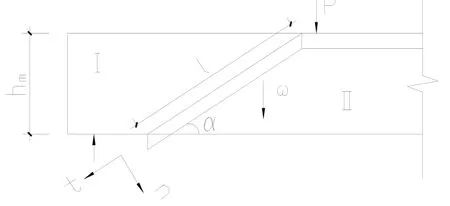
图8 塑性破坏机构Fig.8 The Plastic Failure Model

由几何关系有

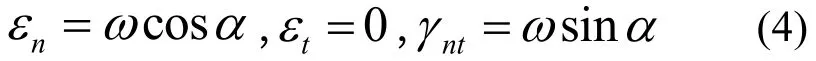
抗剪加固带屈服时，

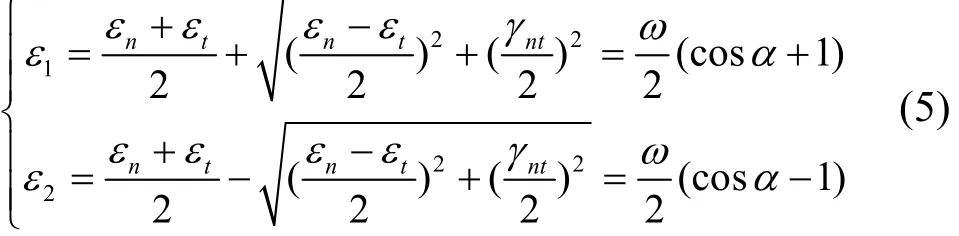
混凝土与钢纤维砂浆所做内功为：

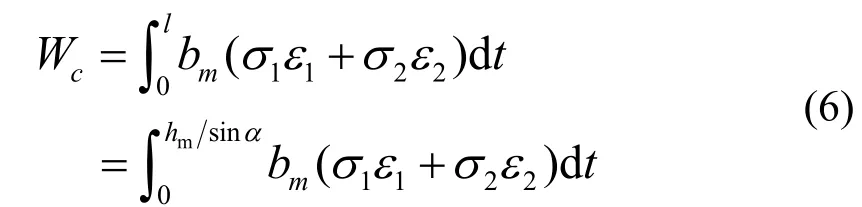
箍筋所做内功为:

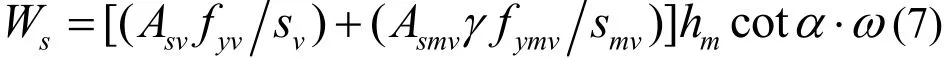
外荷载所做功为：

由虚功原理知：

式中：svA 、smvA 分别为原梁箍筋面积、加固横向钢筋面积，yvf为原梁箍筋屈服强度，ymvf 为加固横向钢筋屈服强度，γ为考虑加固薄层横向钢筋应力发挥不均匀性的抗剪系数[10]，为安全起见，此处γ=0.9，vs、mvs 分别为原梁箍筋和加固横向钢筋间距．联立(2)～(3)、(5)～(9)式有：

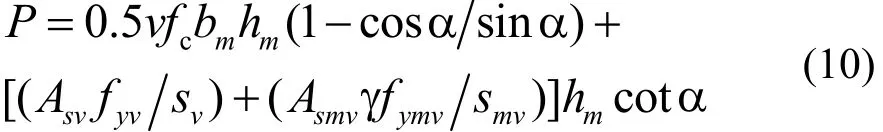
P的极值即为结构上限解，求P极值，对(10)求导，

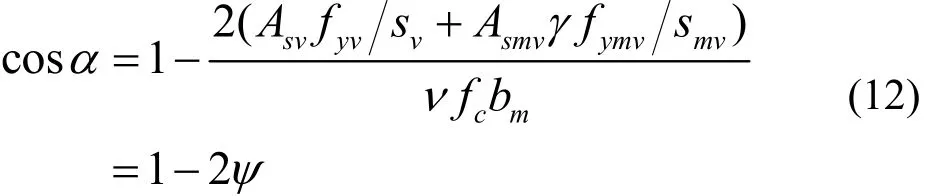
其中：

将P的塑性上限作为抗剪极限承载力计算公式，故钢纤维砂浆钢筋网抗剪加固带抗剪极限承载力为：

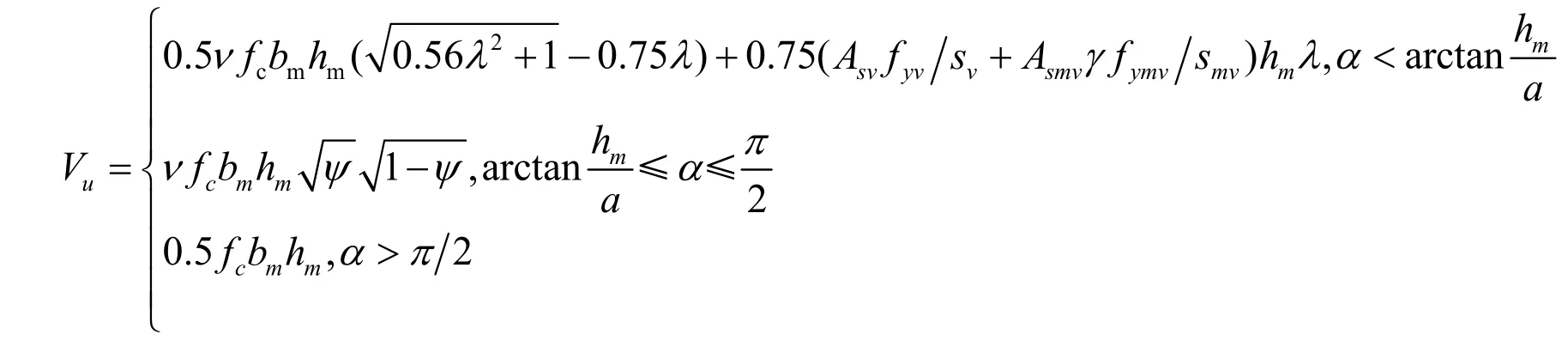
其中： α =arccos(1 -2ψ)、

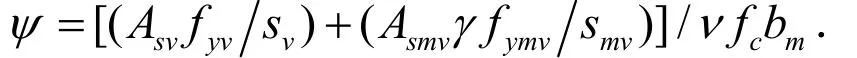
3.3 抗剪承载力试验值与理论计算值

采用塑性分析所得抗剪加固带抗剪极限承载力比传统桁架-拱模型计算承载力高，但均小于试验值．抗剪加固带抗剪承载力试验值与计算值见表4．结果表明，计算值与试验值吻合较好，由于未对结构塑性下限分析，计算公式有待进一步研究．

表4 理论计算值与试验值比较Tab.4 Comparison between calculated and testing value

4 结论

(1)钢纤维砂浆钢筋网抗剪加固带中加固横向钢筋和原箍筋的应变基本同步变化，加固层和原构件协同工作良好，可一定程度上提高伸臂梁的抗剪极限承载力，但剪跨比的不同，加固梁抗剪极限承载力提高幅度差异不大；

(2)钢纤维砂浆钢筋网抗剪加固带可阻滞裂缝发展，提高开裂荷载，使裂缝细而密，增加构件抗裂性能；

(3)钢纤维砂浆钢筋网抗剪加固带可增加梁刚度、延性；

(4)塑性法所得RC伸臂梁钢纤维砂浆钢筋网抗剪加固带抗剪极限承载力计算公式具有一定的安全储备，承载力计算值与试验值差异不大，值得科研工作者更深层次研究．

References

[1] 曹双寅, 邱洪兴, 王恒华. 结构可靠性鉴定与加固技术[M].北京:中国水利水电出版社, 2002: 1-3.CAO Shuangyan, QIU Hongxing, WANG Henghua. The evaluation of structural reliability and reinforcement technique[M].Beijing: China's Water Conservancy And Hydropower Press,2002:1-3.

[2] 史庆轩, 王鹏, 王秋维. 桁架-拱模型用于钢筋混凝土梁的受剪承载力计算分析[J].土木建筑与环境工程.2013(04): 7-12.SHI Qingxuan, WANG Peng, WANG Qiuwei. The truss arch model for calculation and analysis of reinforced concrete beams shear capacity [J]. civil engineering and environmental engineering.2013 (04): 7-12.

[3] 卜良桃, 曾坚, 李为.钢纤维水泥砂浆钢筋网加固 RC梁抗剪试验研究[J].湖南大学学报, 2012, 39(02): 7-11.BU Liangtao, ZENG Jian, LI Wei. Shear behavior of RC beams strengthened by steel fiber ferrocement mortar [J].Journal of Hunan University, 2012,39(02):7-11.

[4] 卜良桃、汪文渊.RC伸臂梁采用PVA-ECC加固抗剪试验研究[J].湖南大学学报. 2014(06): 52-56.BU Liangtao, WANG Wenyuan. Shear behavior of RC overhanging beams strengthened with PVA-ECC [J].Journal of Hunan University.2014(06):52-56.

[5] 易治民、陈升平.钢丝网钢纤维砂浆加固钢筋混凝土梁试验研究[J].湖北工业大学学报. 2013(04): 45-48.YI Zhimin, Chen Shengping. Wire mesh-Steel fiber mortar reinforced concrete beams in bending test research[J]. Journal of Hubei University of Technology,2013(04):45-48.

[6] 张宏战,黄承逵,张瑞瑾.钢纤维高强混凝土箍筋梁抗剪性能试验[J].哈尔滨工业大学, 2006,38 (10) :1782-1785.ZHANG Hongzhan, HUANG Chengkui, ZHANG Ruijin. Experimental study on shear resistance of steel fiber reinforced high strength concrete beams[J]. Journal of Harbin Institute of Technology, 2006, 38(10) :1782-1785.

[7] GB/T50152-2012. 混凝土结构试验方法标准[S].北京:中国建筑工业出版社,2012.GB/T50152-2012. Code for test of concrete structures[S].Beijing: China Architecture and Building Press,2012.

[8] 米海珍,胡燕妮.塑性力学[M].清华大学: 清华大学出版社,2014:10-55.MI Haizhen, HU Yanni. Plastic Mechanics[M]. Tsinghua University: Tsinghua University Press, 2014:10-55.

[9] 刘立新. 钢筋混凝土深梁、短梁和浅梁受剪承载力的统一计算方法[J]. 建筑结构学报. 1995, 16(4):13-21.LIU Lixin. An unified calculation method for shear capacity of R. C. deep beams, short beams and shallow beams[J]. Journal of Building Structures, 1995,16(4):13-21.

[10] 曾令宏,尚守平,万剑平,等.复合砂浆钢筋网加固约束梁抗剪性能试验[J].桂林工学院学报,2008,28(01):34-38.ZENG Linghong, SHANG Shouping,WAN Jianping, et al. Reinforced concrete beams shearthened with high-performance ferrocement[J]. Journal of Guilin University of Technology,2008,28(01):34-38.

[11] 蒋大骅. 钢筋混凝土梁抗剪强度的塑性解[J]. 同济大学学报. 1979,(5):29-43.JIANG Dahua. Plastic solution of reinforced concrete beams in shear [J]. Journal of Tongji University, 1979 (5):29-43.