基于Fluent新型饲料粉碎机结构优化分析
■ 曹 媛 汪建新 曹丽英
(1.内蒙古科技大学机械工程学院,内蒙古包头014010;2.包头轻工职业技术学校,内蒙古包头014010)
在锤片式饲料机的粉碎过程中,工作效率受到多方面的影响,其中粉碎室内风力的大小是影响粉碎速度的主要因素之一,针对这个问题,本文提出了一种加肋板的饲料粉碎机结构。为了验证优化后的饲料机的粉碎效果,本文采用FLUENT数值仿真模拟的方式对饲料机不同入口速度下的流场进行了数值仿真模拟分析,分析过程采用三维计算的形式,保证了计算的精度,并使用UDF动网格的形式控制锤片的运动,使数值计算结果和实际情况更加接近,为饲料粉碎机结构形式的优化设计提供了技术参考。
1 饲料粉碎机优化三维模型设计
本文设计的饲料粉碎机属于较为复杂的几何模型,如图1所示是饲料粉碎机三维结构示意图。饲料粉碎机主要有五部分构成,包括锤片、粉碎室、进料口、出料口和回料口,为了提高饲料粉碎机的粉碎效率,增加粉碎室内部的风力,因此在粉碎室的锥片上添加了肋板。
1.1 饲料粉碎机三维模型
为了提高饲料粉碎机的粉碎效率,增加粉碎室内部的风力,因此在粉碎室的锥片上添加了肋板,如图2所示。该结构是在锥片上增加肋板后将增加粉碎室的粉碎室内的风力,从而提高粉碎效率。
1.2 饲料粉碎机的网格模型
将建立的几何模型导入到Gambit软件中,对模型进行网格划分,得到的网格如图3所示。采用UDF动网格的方法对饲料粉碎机的锤片运动以及粉碎室内的流场进行仿真模拟,动网格采用可以更新的网格,因此采用四面体网格形式,如图3所示,网格划分总数为80万。
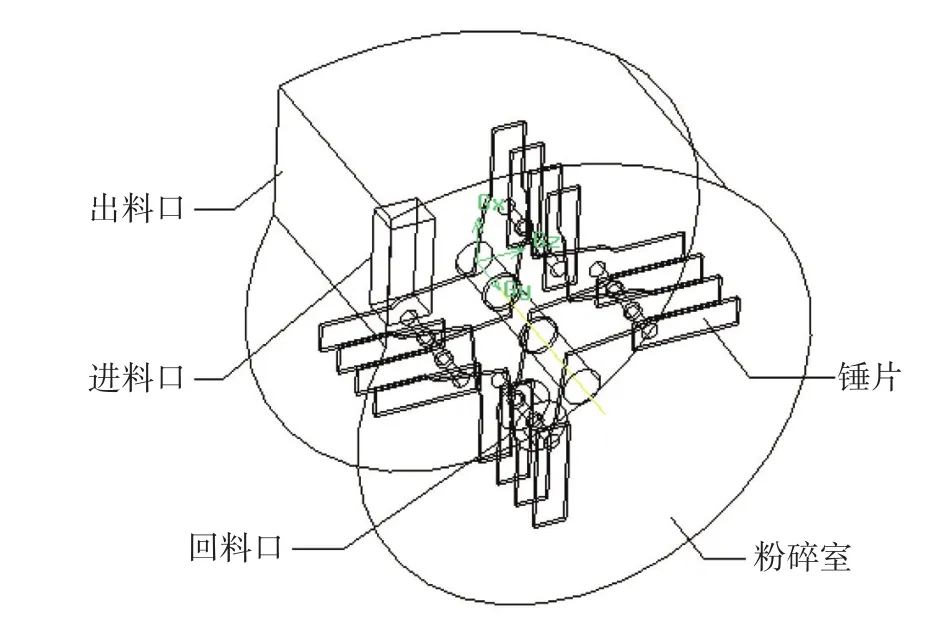
图1 饲料粉碎机结构

图2 无肋板和有肋板粉碎机锥片

图3 饲料粉碎机网格
2 饲料粉碎机计算
2.1 流场计算
在FLUENT计算过程中涉及的主要物理方程包括质量守恒和动量守恒方程,当系统中涉及到能量传递时,还需要使用能量守恒方程。本文在饲料粉碎机粉碎室的流场计算中主要使用了质量守恒方程和动量守恒方程,其中质量守恒如公式(1)所示。

该方程是质量守恒的总的形式,可以适合可压和不可压流动。源项Sm是稀疏相增加到连续相中的质量,或者用户自定义的质量源项。惯性坐标系下,i方向的动量守恒方程为:
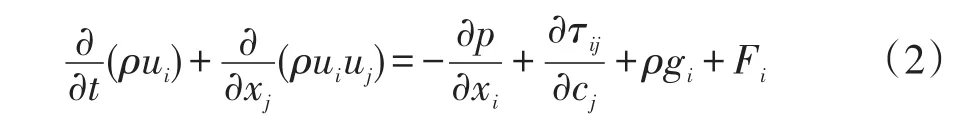
式中:p是静压;τij是应力张量,其表达式如公式(3)所示。
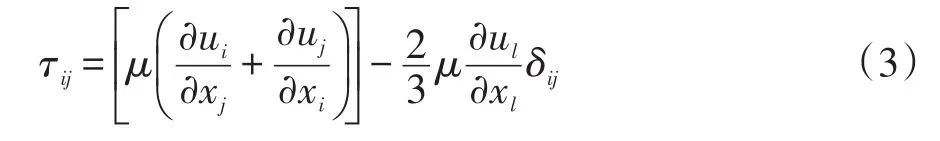
式中:ρgi,Fi是重力体积力和其它体积力,如源于两相之间的作用,Fi还可以包括其它模型源项或者用户自定义源项。
2.2 UDF动网格模型算法及程序设计
本文使用的动网格方法主要是弹性光顺法,该方法将网格系统看作由节点之间用弹簧相互连接的网络系统,初始网格就是系统保持平衡的弹簧网络系统。任意一个网格节点的位移都会导致与之相连接的弹簧中产生弹性力,进而导致临近网格点上的力平衡被打破。由此波及出去,经过反复迭代最终整个网格系统达到新的平衡时,就可以得到一个变形后的、新的网格系统。
在弹性光顺法的参数中,弹性因子(Spring Constant Factor)是介于0到1之间的一个常数,其中0表示弹簧没有阻尼作用。边界节点松弛(Boundary Node Relaxation)则是一个类似于亚松弛因子的参数,每次迭代后新的网格坐标值都等于原坐标加上边界节点松弛与坐标增量的积,缺省设置为1。其余两个参数则是网格迭代计算的控制参数,一个是容差(Convergence Tolerance),另一个是迭代次数(Number of Iterations)。其中锤片的运动采用UDF编程的方式进行控制,运动后的网格采用自动更新的形式,UDF主要编程如下:

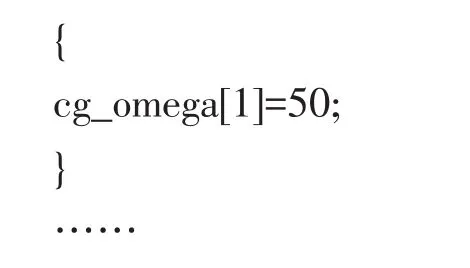
3 饲料粉碎机粉碎室三维数值仿真模拟研究
为了验证第二节设计的数学模型算法和UDF编程的有效性和可靠性,本节以粉碎室速度场的仿真模拟为例,对加肋板和不加肋板两种结构形式的粉碎室进行数值计算,其具体步骤如下。
图4表示FLUENT三维仿真模拟的主流程图,计算过程主要包括前处理、迭代计算和后处理三部分。其中前处理主要包括三模模型的建立和网格的划分,迭代计算包括边界条件的设置和迭代计算,后处理部分包括计算处理和结果处理,通过对计算结果的分析,将其作为反馈信息反馈给计算处理部分,利用边界条件的调整和时间步长的调整,重新迭代计算,提高计算的精度。计算过程中主要使用的边界条件的设置如表1所示。

图4 FLUENT三维仿真模拟流程

表1 边界条件设置参数
表1表示主要的边界条件参数设置,包括入口、出口、回料口和湍流模型的设置,多相流模型采用Mixture模型,其他边界条件设置保持默认边界条件,通过计算得到的速度场云图如图5所示。
图5表示在Z=0.2 m截面处,当入口速度为10 m/s时两种结构的速度场分布云图,由图5可以看出,在转轴中心处和粉碎室的最外侧存在最大速度,这与饲料粉碎机实际工作的情况相符合,从而验证了数值仿真模拟的准确性和可靠性。
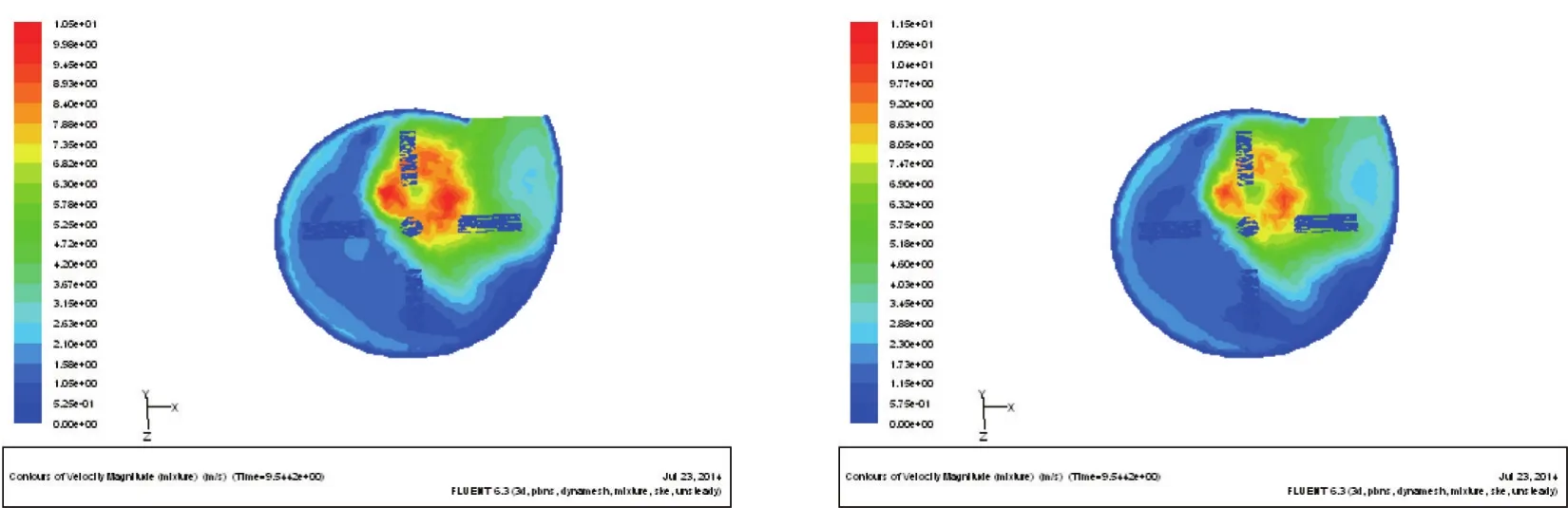
图5 10 m/s时速度分布云图
图6表示在Z=0.2 m截面处,当入口速度为15 m/s时两种结构的速度场分布云图,由图6可以看出,随着速度的增大,两种结构的最大速度都有所增大,并且增加肋片结构速度的增大幅度要明显大于不加肋片结构。
图7表示在在Z=0.2 m截面处,当入口速度为20 m/s时两种结构的速度场分布云图,由图7可以看出,随着速度的增大,两种结构的最大速度依然都有所增大,并且增加肋片结构速度的增大幅度也要明显大于不加肋片结构。

图6 15 m/s时速度分布云图
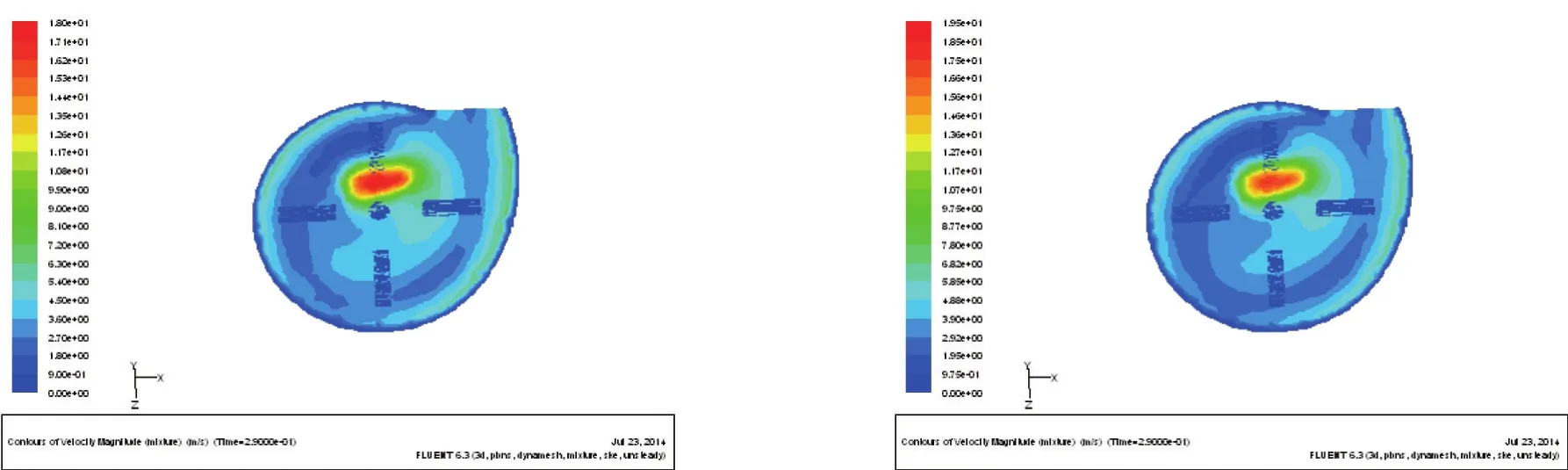
图7 20 m/s时速度分布云图
将不同速度条件下的速度计算数值统计成表2的形式,表2显示在不同入口速度条件下饲料粉碎机粉碎室的最大速度值结果表,由表2可以看出,随着入口速度的增大,两种结构形式的最大速度数值都有所增大,其中有肋板结构的最大速度值明显大于无肋板结构,从而提高了粉碎的机械效率。

表2 不同入口速度条件下流场速度最大值(m/s)
4 结论
通过计算得到了不同速度条件下的速度场分布云图,并且对最大速度值进行统计发现,增加肋片后的结构最大速度数值明显大于不加肋片的结构,从而提高了饲料粉碎机工作的机械效率,为饲料粉碎机结构的优化设计提供了技术参考。

