蜗壳座环与固定导叶焊接过渡圆角处有限元子模型法仿真

张 敏，赵 斌

（1. 河南机电高等专科学校 机电工程系，河南 新乡 453003 2. 河南机电高等专科学校 电气工程系，河南 新乡 453003）

0 引言

蜗壳座环是水轮机主要的引水部件之一，也是埋入混凝土中的大型隐蔽设施之一，其结构型式不仅要考虑它的导水性能，还要有足够的强度和刚度以保证机组安全稳定运行。这样对蜗壳和固定导叶的刚强度就提出了严格的要求，那么如何精确计算出部件的应力水平就成为发展水电技术的一个不可缺少的重要环节。通常我们在进行有限元结构分析时，某些细节部分在实体造型过程中往往不予考虑，这是受到计算机容量、分析软件精度及计算时间等因素的限制。但是这样处理往往会造成计算结果中出现局部高应力区

域。在进行蜗壳座环有限元分析时，就遇到这样的情况，座环环板与固定导叶连接处的焊接过渡圆角相对于整个结构尺寸来说很小，因此，在建立有限元计算模型中时往往不考虑该处的焊接过渡圆角，这样造成该处的应力水平较高，出现了由于几何不连续产生的峰值应力。而由于实际结构中存在焊接过渡圆角，实际结构的应力水平要低于没有考虑焊接过渡圆角的有限元分析计算结果。 结构分析软件ANSYS中的子模型功能很好地解决了这个问题，本文为获得蜗壳座环与固定导叶焊接过渡圆角处的真实应力水平，结合蜗壳座环装配结构，利用ANSYS软件的子模型分析模块对焊接过渡圆角处应力水平进行计算研究，并与原始计算结果进行比较。

1 子模型原理

子模型法是有限元法的一项高级分析技术，在解决复杂应力应变问题时有其无可比拟的优点。我们在用有限元法进行结构分析时往往会遇到这种情况，即对于某些关心的区域，如尺寸相对较小区域，如果网格划分得太稀疏就无法得到满意的结果，体现不出小尺寸位置的真实应力水平，而这“稀疏”的网格对于其他区域来讲密度已经足够了。

针对上面提到的问题，有两种解决方法：第一采用更密一些的网格划分整个模型并进行计算，第二只在关心的区域采用细密网格划分并对关心区域进行分析。显而易见，第一种方法影响计算速度，耗费时间，无法提高工作效率，第二种方法描述的即为子模型技术。

子模型法也可称为切割边界法，是一种基于圣维南原理精确计算结构中的细部构件的方法。ANSYS提供的子模型技术首先需要在原有整体模型上进行计算，在整体分析结果的基础上，截取关心区域模型，在截取模型上倒出过渡圆角，然后采用合适的尺寸划分出更精细的网格。把原有模型的位移强制施加到局部模型的在切割边界上，接下来就可以进行分析求解，这样就获取了关心区域上精确的应力计算结果。需要注意的是在子模型与原模型的分析计算中要始终保证切割边界上的位移一致，即原有模型切割边界的计算位移是子模型的边界条件。

子模型分析主要有以下5个步骤：

（1）生成较稀疏的网格并进行分析。不考虑局部区域，也就是对整体结构进行建模并分析，模型网格相对于后面提到的子模型来说是较粗糙的。

（2）生成子模型。截取部分整体模型提取出子模型，使用与整体模型相同的单元类型划分网格。

（3）提供切割边界插值。这是子模型的关键步骤，对于子模型切割边界上的结点，程序用整体模型网格中相应的单元确定自由度数值，然后插值到切割边界上。

（4）进行子模型分析。选择分析类型、选项并施加载荷，然后求解子模型。

（5）验证切割边界选取是否正确。用比较切割边界上的结果与整体模型相应位置的结果是否符合来验证。如果结果符合得很好，证明选取的切割边界是正确的。如果符合不好的话，就要重新定义离关心区域更远一些的切割边界重新生成子模型和重新计算。

对于结构子模型，还需要注意的是它只对实体单元和壳单元有效。

ANSYS子模型方法已经成功应用到很多领域，水轮机部件强度计算中也涉及到了子模型技术，例如转轮和球阀刚强度计算中，子模型技术已经得到了验证。

2 蜗壳座环有限元计算

2.1 单元选择

建模时全部采用三维实体块体单元，为保证计算精度，对于一些简单的结构区域采用20节点六面体单元，而对于几何形状复杂区域，采用10节点四面体单元；其中，六面体单元和四面体单元采用五面体塔形单元过渡，如图1所示。

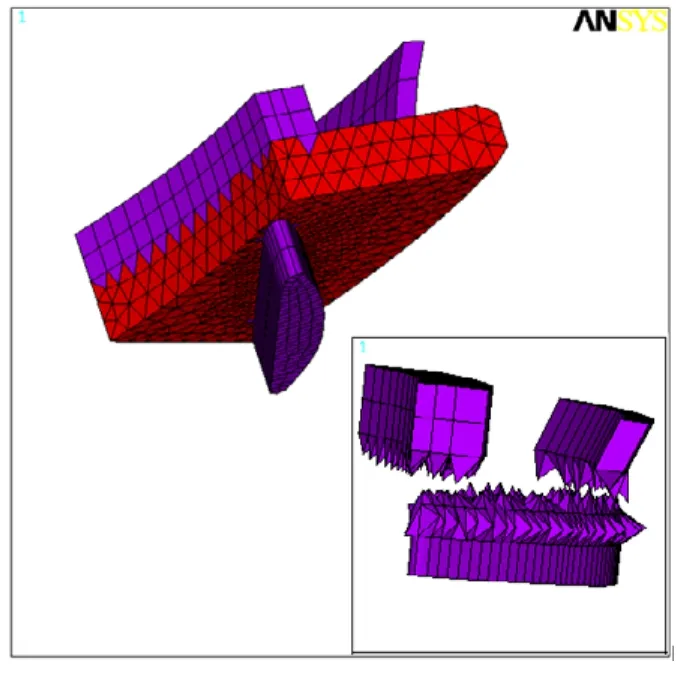
图1 单元转变后的结果显示

2.2 计算模型

以某电站蜗壳座环作为算例，对于蜗壳座环来说，金属蜗壳部分是由进水口端到尾端各个断面逐渐缩小的蜗形状。一般情况下，高应力出现在进水口端，因此分析时把蜗壳看作以第一断面（进水口断面）为基础的等断面环壳，假定为周期对称结构；座环是一个周期对称结构。所以在建模时取以蜗壳进水口段为基础的包含一个固定导叶在内的2π/n（n为固定导叶个数）的扇形区域作为分析模型，包括：上下环板、一个固定导叶、蜗壳，此时没有考虑上下环板与固守导叶间的焊接过渡圆角，不考虑混凝土对蜗壳的影响。有限元计算模型如图2所示。

图2 有限元计算模型

边界条件：在蜗壳座环切开断面处施加周期对称边界条件，使相应节点保持位移协调一致；约束蜗壳座环与混凝土基础把合螺栓分布圆处相应节点的Z向自由度，此外在上下环板处各取一节点约束 θ向自由度，来防止产生刚体位移。

有限元计算最大应力值及应力出现位置见表1。

表1 有限元计算结果

有限元分析应力分布如图3所示，从图中可以看出：座环上环板与固定导叶焊接处为最大应力出现位置，因该处没考虑焊接过渡圆角，所以产生了由于几何不连续而生成的峰值应力；在实际结构中该处是存在焊接过渡圆角的，所以需要采用子模型技术对此处进行不同焊接过渡圆角下有限元分析，进而得到该处的真实应力水平，并凭计算结果确定可能施加的最小焊接过渡圆角，以保证结构的应力水平满足设计要求。

图3 整体模型应力分布图

3 峰值应力区域的子模型分析

根据子模型分析原理和计算步骤，选取作为子模型的局部区域一定要远离焊接过渡圆角，如图4所示。有限元网格采用SOLID92四面体单元。在过渡圆角处采用合适尺寸的单元长度，使网格由密到疏，以保证计算精度和确保过渡圆角的真实性，有限元网格剖分图如图 5所示。作为对比计算和指导焊接量，本次计算对三种不同的焊接过渡圆角进行了子模型法分析，计算结果见表2。

图4 截取的子模型区域

图5 子模型有限元计算图

表2 不同过渡圆角子模型计算结果

从表2我们看出，运用子模型法考虑过渡圆角后计算出的最大应力值比原来降低了，得到了过渡圆角处的真实应力值；随着固定导叶与上环板之间焊接过渡圆角的增加，固定导叶与环板之间的应力呈下降趋势，说明适当增加固定导叶和环板之间的过渡圆角，可以降低该区域的应力水平。但是，固座环板与固定导叶处的过渡圆角是通过焊接堆焊而成，过大的过渡圆角会增加焊接量易产生过高的焊接残余应力，反而会加大局部应力水平。因此，对于该处过渡圆角的确定，除要考虑该处的应力水平外，还应考虑焊接因素的影响以及结构的可行性等因素，从而确定一个合理过渡圆角尺寸。图6为子模型分析应力分布图。

4 结论

（1）运用ANSYS软件的子模型模块能计算出复杂结构局部区域的真实应力水平，很好地满足了实际工程的需要。

（2）座环环板与固守导叶连接处适当的过渡圆角，可以有效降低该区域的应力水平。在考虑焊接因素情况下，采用子模型分析方法，可以确定合理的过渡圆角尺寸。

[1]吕桂萍, 唐任远. 混流式转轮子模型方法研究[J].大电机技术, 2003,(5).

[2]阳芳, 伍鹤皋. 大型水轮机蜗壳结构动静力分析[J]. 武汉大学学报, 2004,(5).

[3]王燕. 子模型方法在活门有限元分析中的应用[J].大电机技术, 2010,(4).

[4]叶先磊, 史亚杰. ANSYS工程分析软件应用实例[M]. 清华大学出版社, 2003.