一种主客观结合的属性权重确定方法

□ 陈燕云 季 丹 邱建林

一、引言

权重确定在决策过程中非常重要，它体现了各个属性在评价过程中的地位，直接关系到最后的决策结果。目前已有许多专家学者对权重确定进行了研究，比较常用的权重确定方法有模糊统计法、主观赋值法如Delphi法、二元对比排序、模糊判断矩阵法等等。单一的权重确定法或者偏主观，或者又过于依赖于数据，因此都无法全面反映属性的重要程度。本文提出一种将偏主观经验的灰色关联度法和“凭数据说话”的粗集权重确定法相结合的主客观集成权重确定方法，在一定程度上改善了单一权重确定法的不足。

二、基于粗糙集理论的权重确定方法

常见的基于粗集理论的权重确定方法是通过计算决策属性对条件属性的依赖度来确定属性的重要度，进而确定属性权重的。具体步骤如下:

决策系统S=(U，A，V，f)，A=CYD 是属性集合，C是条件属性，D是决策属性，则C与D之间的依赖度γc(C，D)为:

γc(D)表示了由条件属性C的取值能准确判定出属于某个决策属性D的等价类的对象所占系统的比例。任意cj∈C对D的重要性定义为:sigDC-{cj}=γ(C，D)-γ(C-{cj}，D)。

这说明属性cj∈C的重要程度可由去掉c后所引起的决策属性依赖度变化的大小来度量。

第j个属性cj的权重

目前已有不少算法对该经典算法作出了改进。文献综合考虑了属性集中条件属性的整体重要度和个体重要度，改善了常见冗余属性为0引起的矛盾。文献在考虑冗余属性权重的同时通过设置高级优先队和低级优先队来避免出现冗余权重大于非冗余权重的情况，确保权重的合理性。

然而有时候我们求信息系统的权重，即数据表中没有决策属性，需要单从条件属性出发解决权重的分配问题。

本文采用基于条件信息熵的权重确定方法，具体步骤如下:

设信息系统 S=(U，A)，A={A1，A2，Λ，An}，令 X=U/IND(Aj)={X1，X2，Λ，Xm}表示等价关系 IND(Aj)在 U 上的划分，

定义属性Aj的信息熵H(Aj)为:

H(Aj)=-∑mi=1P(Xi)log2(P(Xi))

进而，属性Aj的权重定义为:

总之，基于粗糙集理论的权重确定方法完全是由数据决定的，比较客观，但粗糙集理论对样本数据的要求比较高，如果样本数据不具有代表性，其决定的权重也会偏离实际。

三、灰色关联度权重确定方法

经典的灰色关联度权重确定步骤如下:

(一)构建评价矩阵A，并无量纲化处理得矩阵C。

A=(aij)n×m;

Cij(k任意确定，且aik≠0)

(二)求取属性两两之间的关联度并构建关联度矩阵R。

εij(一般 =0．5)

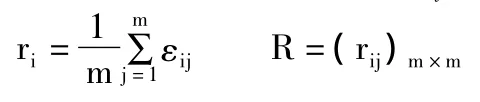
(三)计算各属性的权重。

该算法中分辨系数ρ的取值具有主观不确定性，使得灰色关联度算法受专家决策的影响较大。

四、综合权重的确定

综合权重wj=αφj+(1-α)φj;α为经验因子。

可以通过设置经验因子，调整主观权重和客观权重的比重。

五、应用

我们以属性约简后的玉米样本集为例，将上述提出的主客观集成权重确定算法应用到玉米良种选育当中，如表1所示，共有7个属性，51个对象。

表1 玉米样本集

(一)求粗糙集权重。七个属性的信息熵分别求得为:1．3325、1．5736、1．5833、1．5699、1．5427、1．5801、1．397。

求得结果见表2。

表2 粗糙集权重

(二)灰色关联度权重。

1．求取标准化矩阵。因为各属性的量化值所在的区间不完全相同，因此首先要进行无量纲化处理，这里令第一行属性值为1，其余行属性值，结果见表3。

表3 标准化矩阵

2．构建关联度矩阵。如表4所示。

表4 关联度矩阵

全生育期 1 0．53814 0．6303 0．6439 0．548 0．6435 0．6138穗高 0．5381 1 0．5761 0．5293 0．6584 0．516 0．651穗粗 0．6303 0．5761 1 0．587 0．5783 0．6276 0．6141行粒数 0．6439 0．5293 0．587 1 0．5408 0．6801 0．5839千粒重 0．548 0．6584 0．5783 0．5408 1 0．5385 0．6115出籽率 0．6435 0．516 0．6276 0．6801 0．5385 1 0．599小区产量 0．6138 0．651 0．6141 0．5839 0．6115 0．599 1

3．各属性的灰色关联度权重。如表5所示。

表5 灰色关联度权重

(三)综合权重。令 α =0．5，则 ω =0．5φ +0．5φ，因而综合权重为:

表6 综合权重

三个权重对比见表7。

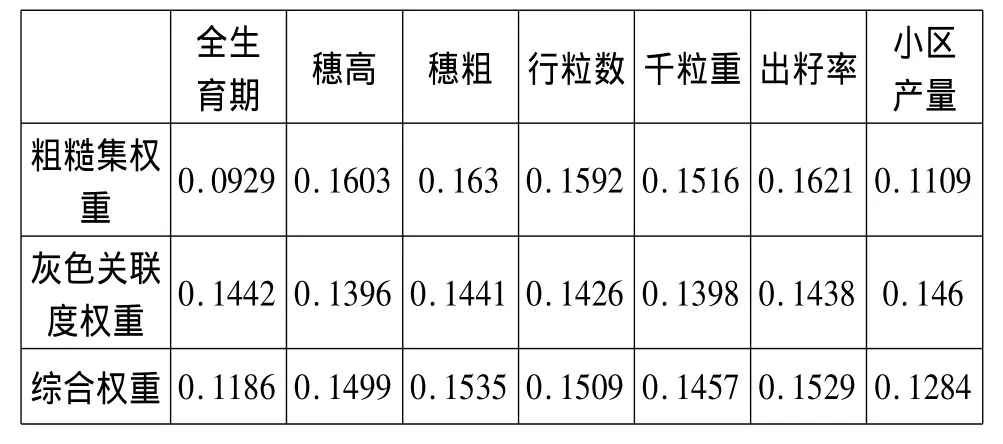
表7 权重对比

可以看出粗糙集权重和灰色关联度权重的侧重点并不相同，具有互补性，将它们结合起来得出的综合权重更具合理性和实用价值。

六、结语

单一的赋值法在效果上或者偏主观或者偏客观，本文选取偏主观的灰色关联度权重确定法和偏客观的粗糙集权重确定法，将两者有效结合从而确定信息系统的综合权重，在一定程度上改善了单一赋值法的不足，提高权重的合理程度，从而使最终决策更加准确。但文中经验因子的设置不够科学，需要进一步研究。

［1］Mareschal B．Weight stability intervals in multi-criteria decision［J］．European Journal of Operational Research，1998

［2］周宇峰，魏法杰．基于模糊判断矩阵信息确定专家权重的方法［J］．中国管理科学，2006

［3］鲍新中，刘澄．一种基于粗糙集的权重确定方法［J］．管理学报，2009

［4］朱红灿，陈能华．粗糙集条件信息熵权重确定方法的改进［J］．统计与决策，2011

［5］邹永红，谭建林．基于综合灰色关联度加权法的玉米品种评价［J］．南方农业学报，2011