应用于波束域的改进TOFS算法∗

(国防科技大学自动目标识别重点实验室,湖南长沙410073)

0 引言

信号波达方向(Direction-of-Arrival,DOA)估计是阵列信号处理的重要研究课题之一,广泛应用于雷达、移动通信、声纳、导航等各个领域[1-3]。作为现代高分辨DOA估计算法中的经典代表,多重信号分类(Multiple Signal Classification,MUSIC)算法[4]30年来得到了迅速的发展[5-7]。但是,常规的阵元域MUSIC算法不能处理相干信号,并且只局限于窄带信号处理范围。而现代电磁环境更加复杂,信号愈加密集,同时由于多径传输等因素的影响,实际场合中存在大量的宽带相干信号,怎样去除多径效应是波达方向估计领域的重要课题[8],传统的窄带高分辨测向算法已经不能满足需要,所以研究宽带相干信号环境下的目标方位估计问题具有实际意义。

比较经典的宽带信号高分辨算法主要有两种:非相干信号子空间(Incoherent Signal-Subspace Method,ISM)方位估计方法和相干信号子空间(Coherent Signal-Subspace Method,CSM)方位估计方法[9]。ISM算法是最基本的宽带空间谱估计算法,CSM算法在其基础上增加了聚焦的过程,虽然提高了低信噪比条件下的估计性能,但聚焦矩阵的构造需要预先估计目标方位,预估角度的偏差对精度影响较大。投影子空间正交性测试(Test of Orthogonality of Projected Subspace,TOPS)方法[10]是一种无需预估过程的宽带信号空间谱估计方法,但其参考频点上信号子空间估计的不准确性会影响整个算法的性能[11]。为解决该问题,文献[12]提出了一种频域子空间正交性测试(Test of Orthogonality of Frequency Subspace,TOFS)算法,该方法通过角度和频率构造向量,判断该向量和各个不同频点上噪声子空间的正交性程度来进行角度估计,因为该方法利用了每个频点上的信息,所以避免了TOPS算法中由于参考频点的估计误差而给整个算法带来的影响。虽然TOPS与TOFS算法都不用事先预估角度,但它们都不能对相干信号进行有效估计。本文将矩阵共轭重构算法引入到TOFS算法中,提出了一种改进的TOFS算法,从而实现宽带相干信号环境下的DOA估计,并且具有较好的分辨性能。

前文提及的宽带信号空间谱估计算法都是建立在阵元空间基础上的,存在运算量大的缺点,对于大阵列数目、小信源数目的情况,可以采用波束空间DOA估计算法,将信号从阵元空间变换到波束空间中进行处理,从而降低运算复杂度。本文在对TOFS算法改进的基础上,将其从阵元域变换到波束域中,降低了运算量,并且未影响其在相干信号环境下的估计精度。

1 均匀线阵下的信号接收模型

假设接收基阵是阵元数目为M的均匀线阵(ULA),且各阵元是各向同性的,阵元间距d为入射信号最高频率对应波长的一半,空间中有P个信号入射到此线阵上,入射方位角分别为θ1,θ2,…,θP,第m个阵元的接收数据可表示为

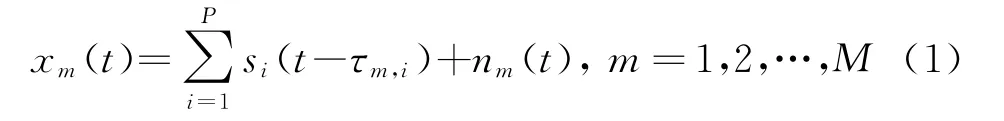
式中,nm(t)为第m个阵元的空间白噪声,τm,i为信号si(t)到达第m个阵元相对于其到达参考阵元的时延,表达式如下:

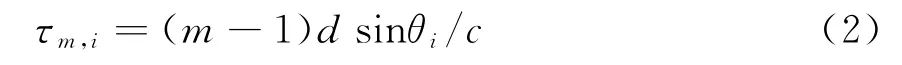
将接收数据分为K段,对每段进行J点的DFT变换,则阵列输出在频域上可表示为

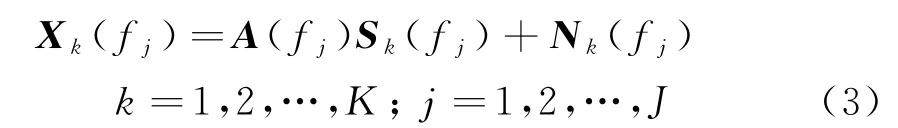
式中,Xk(fj),Sk(fj),Nk(fj)分别为频率fj处对应的接收数据、信号和噪声的频域,A(fj)为M×P维的阵列流形矩阵,表达式为

综上分析,式(3)即为宽带信号均匀线阵下的接收模型。

2 正交性测试方法

2.1 TOPS算法

下面首先引入两个引理和一个定理[10]。

引理一:对于导向向量a(fi,θi),存在矩阵Φ(fj,θj),使得a(fk,θk)=Φ(fj,θj)a(fi,θi)成立,并且频率和角度满足式(6):

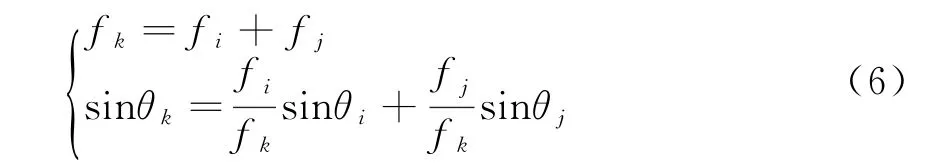
其中,Φ(fj,θj)为对角矩阵,第m个元素可表示为

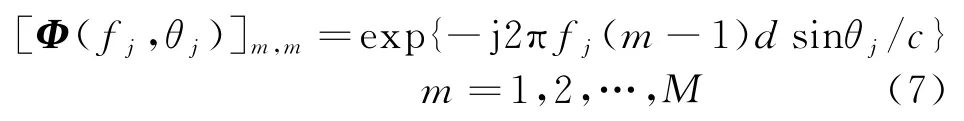
引理一表明,不管频率和角度值为多少,任意一个阵列流形矢量都能通过转换矩阵变换到指定频率上,尤其是当θi=θj时,θk=θi=θj成立,也就是说如果选取一个角度与信号入射方向相同的转换矩阵,那么可以在不改变信号来向的条件下将阵列流形矢量从一个频率搬移到另一频率上。

引理二:当Δf=fj-fi时,下式等号两边的值域空间相同:

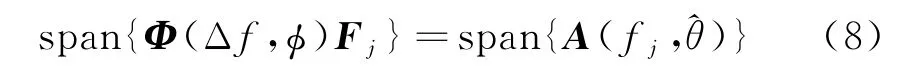
式中,ϕ为假设的信号方位角度,Fj为频点fj处的信号子空间,角度^θ的取值与ϕ有关。

定理:当2P≤M,K≥P+1时,定义M×P的矩阵U(fj,ϕ)如下:

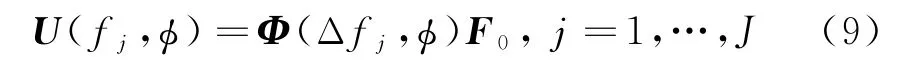
式中,Δfj=fj-f0,F0为参考频点f0处的信号子空间,定义Gj为频点fj处的噪声子空间,接着构造一个P×J(M-P)的矩阵:

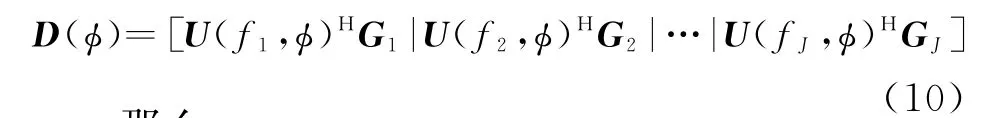
那么:

a)当假定的信号入射角度ϕ与真实入射角度θ相等时,D(ϕ)将缺秩;

b)当假定的信号入射角度ϕ与真实入射角度θ不相等时,D(ϕ)将满秩。

只有在入射信号完全不相关的条件下,上述定理才成立,当信号相干时,信号子空间的维数会降低,此时,无论假定信号是否等于真实入射角,D(ϕ)都将缺秩,TOPS算法无法正常工作。但是由于噪声的存在,子空间估计会出现一定的误差,因而D(ϕ)一般情况下不会出现缺秩的情况,通常采用对D(ϕ)进行奇异值分解的办法来判断D(ϕ)缺秩的程度,进行角度搜索的公式如下:

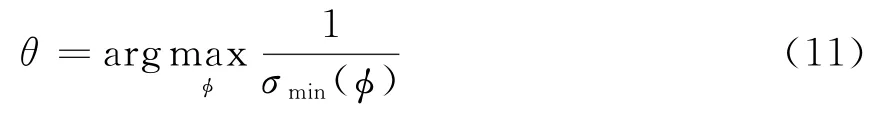
式中,σmin(ϕ)为矩阵D(ϕ)最小的奇异值,θ为信号的方位估计值。

在实际应用中,为了减少信号子空间泄露到噪声子空间,采用投影方法减小D(ϕ)的估计误差,令阵列流形矢量a(fj,ϕ)的投影矩阵P(fj,ϕ)为

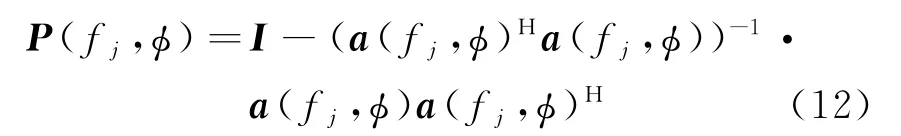
再根据式(10)形成新的矩阵D(ϕ),用U′(fj,ϕ)代替原来的U(fj,ϕ):

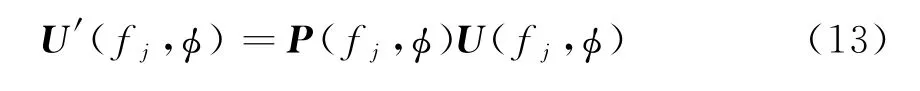
2.2 TOFS算法

由上文所述,因为TOPS算法构造矩阵D(ϕ)的过程是基于某一参考频点上的信号子空间F0,在低信噪比时,参考频点上的信号子空间估计将会存在较大的误差,从而影响整个算法的估计性能。文献[12]对TOPS算法进行改进,提出了T OFS算法,避免了出现伪峰的情况。

与其他经典宽带高分辨算法类似,TOFS算法先对各个频点上的协方差矩阵进行特征值分解,得到各个频点处的噪声子空间Gj,j=1,2,…,J。再由频率和假定的信号方位角度构造导向向量a(fj,ϕ),根据子空间理论,当ϕ为信号方向时,有aH(fj,ϕ)Gj=0。

因而可以构造标量函数U(fj,ϕ)如下:

但是由于受噪声的影响,式(14)的结果不一定会为零,但可以根据其距离0的程度来判断信号方向。接着,将这J个标量U(fj,ϕ)构成一个新的向量:

对ϕ进行一维角度搜索得到信号的方位估计值:

式中,σ(ϕ)表示向量D(ϕ)的二范数,也就是D(ϕ)中元素平方和的平方根。

虽然TOFS算法能消除伪峰,但其低信噪比条件下难以对相干信号进行有效估计。鉴于此,本文第3节将提出一种改进的TOFS算法,使其能够估计相干信号的波达角,同时将改进的算法应用于波束空间来降低算法的运算量。

3 改进的TOFS算法及在波束域的应用

3.1 TOFS算法改进

将矩阵共轭重构算法与TOFS算法结合来处理相干信号,可以得到改进的TOFS方法。设Xk(fj)是频点fj处的接收数据的频域表示,使,其中,JM为M阶矩阵,除了反对角线上的元素为1以外,其余元素为0,具体表示如下:

那么可以求得Yk(fj)的自相关矩阵为

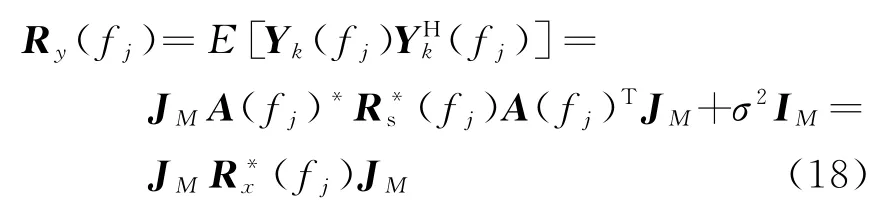
令矩阵D为

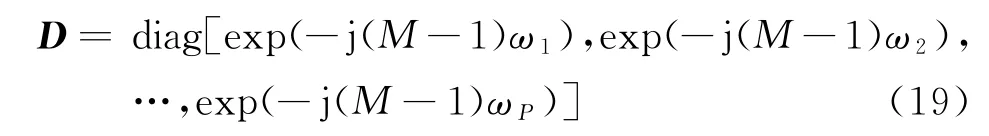
式中,ωi=dfjsin(θi)/c,则有下式成立:

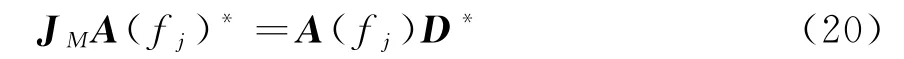
对于非相干信号,Rs为实对角阵,再将式(20)代入式(18),由J2=I及D∗D=I可得

再令

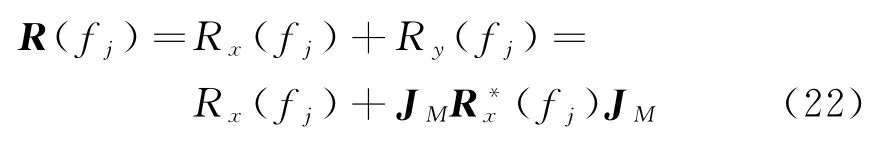
上式中的矩阵R即为解相干以后的协方差矩阵,共轭重构本质上是前后向空间平滑,但实际只构造了一个子阵,并且子阵的阵元数与阵列阵元总数相等,也就是说子阵与原阵完全一样,因而不会损失阵列孔径。空间平滑消除了因信号相干而导致的协方差矩阵Rx的奇异性,所以采用矩阵R作为后续估计的协方差矩阵能够对相干信号进行有效估计。此外,对单个信号进行到达角估计时,由于协方差矩阵Rx和Ry是采用有限次快拍进行估计的,在信噪比较低和快拍数较少时,误差较大,而采用R进行估计,具有平均的意义,因此可以提高估计的性能,后续仿真也验证了这一结论。

3.2 基于波束空间的改进TOFS算法

虽然改进后的TOFS算法已经具备良好的宽带相干信号处理能力,但其运算量较大,因而会限制其在实际应用中的发展。在阵元数多,信源数少的条件下,可以采用波束域处理的方法[13-14]来降低运算复杂度,即先构造一个波束形成矩阵,以波束域代替阵元域,接着在该波束范围内进行处理。一般情况下,需要形成的波束个数比阵列个数小得多,所以可以采用波束域处理的方法来降低传统阵元域宽带信号空间谱估计算法的运算维度。

波束形成矩阵由B个已知指向的导向矢量来创建:

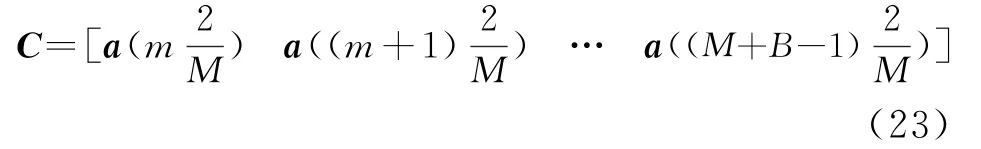
式中,a(θ)为阵列的导向矢量,B为需要形成的波束个数。

当式(23)并非一个正交矩阵时,需要利用下式对其进行正交化:

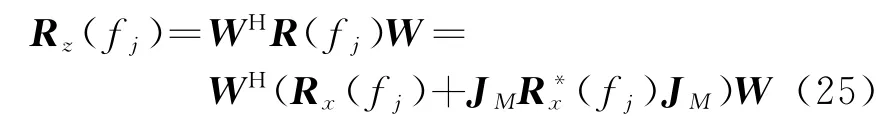
根据前文所述,阵元域的TOFS方法需要进行特征值分解的矩阵Rx(fj)的维度为M×M,因而其运算复杂度为O(M3),而波束域中的改进TOFS方法需要进行特征值分解的矩阵Rz(fj)的维度为B×B,因而其运算复杂度为O(B3),一般说来,M＞B,因此对于阵列数多、信源数小的情况,计算量会大大降低。

综上分析,波束域的改进TOFS算法步骤如下:

① 对接收到的数据进行分段,对每一段进行DFT,得到每一频点下的阵列协方差矩阵;

② 根据式(23)设计出B个波束,构成波束转换矩阵;

③ 在各个频点处用式(22)对Rx(fj)进行共轭重构处理得到R(fj),再利用式(25)将其变换到波束空间中得到Rz(fj);

④ 在每个频率点上对波束空间的协方差矩阵Rz(fj)进行特征值分解,得到噪声子空间;

⑤ 进行角度搜索,根据式(15)对所有可能的方向角度构造矩阵D(ϕ)=[U(f1,ϕ),U(f2,ϕ),…,U(fJ,ϕ)];

⑥ 根据式(16)估计出信号方向。

4 仿真实验及结果分析

实验1 算法相干处理能力的验证

仿真条件:假设接收基阵为40阵元的均匀线阵,阵元间隔为最高频率的半波长,噪声为互不相关的高斯白噪声,两个相干信号的功率相等,入射角度为24°和26°,中心频率为900 MHz,带宽为600 MHz。信噪比取10 dB,采样率为1 200 MHz,信号观测时间为5.12μs,在时域上划分为48段,每段作128点的FFT,得到信号带宽内的频点数为65个。

在验证算法能否处理相干信号之前,首先构造波束转换矩阵,根据3.2节的分析,将弧度换算成角度可知需要形成指向为20.1°,22.9°,25.8°,28.6°和31.5°的5个常规波束,方向图如图1所示。接着利用TOPS算法、TOFS算法以及本文改进的算法对信号进行到达角估计,4种算法得到的空间谱如图2所示。从图中可以看出,TOPS算法和TOFS算法无法分辨出两个相干信号的方位,而改进后的TOFS算法在24°和26°两个信号方位角形成两个谱峰,能准确地分辨出相干信号的方位,并且将算法从阵元空间变换到波束空间中后,形成的谱峰相对前者更加尖锐。

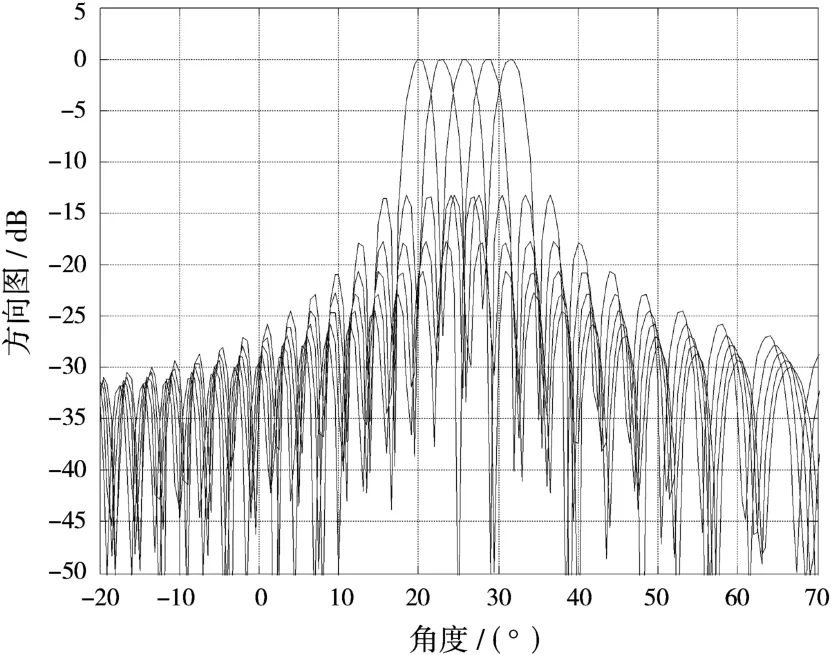
图1 波束方向图

图2 4种算法的空间谱估计结果

实验2 算法测向精度的比较

首先进行单个信号源的测向精度的比较。仿真条件为:单个信号源,入射角度为25°,信噪比变化范围为-20～20 dB,其他实验条件同实验1,进行500次蒙特卡洛仿真。为了更好地说明本文算法的优势,文章对常用的RSS方法和TOPS算法的估计精度也进行了仿真,仿真结果如图3所示,本文利用均方根误差(RMSE)对算法的精度进行衡量,RMSE越小,算法精度越高。从图中可以看出,RSS算法的估计性能比较稳定,但在信噪比较高时明显不如TOPS算法和TOFS算法,这是由于该方法需要预估角度。同时可以看出,改进TOFS算法的测向精度比常规的TOFS算法更高,将改进后的算法应用于波束空间之后,算法估计精度略有降低,但下降幅度很小。

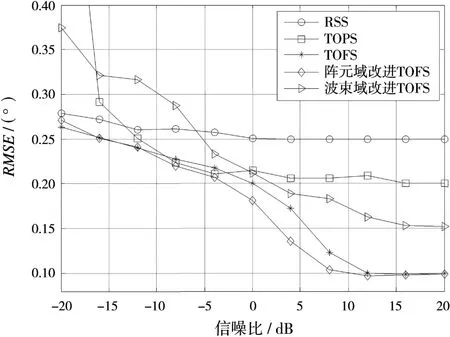
图3 单个信号入射、不同信噪比情况下5种算法的均方根误差

其次对两个相干信号的估计精度进行比较。信号方位和信号参数与实验1相同,信噪比变化范围为-20～20 dB,对其进行500次蒙特卡洛仿真。由图2可知,传统的TOPS算法和TOFS算法没有解相干的能力,因而这里不给出这两种算法的估计精度。从图4可以看出,在信噪比大于4 d B时改进后的TOFS算法性能要比RSS算法更好,当算法应用到波束空间中后,虽然估计精度略有降低,但仍优于RSS算法。

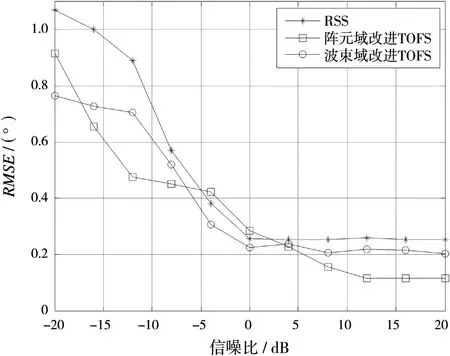
图4 两个相干信号入射、不同信噪比情况下3种算法的均方根误差

实验3 算法运算量的比较

由3.2节的分析可知,将改进后的算法变换到波束空间之后运算复杂度将大大降低,为了验证前文的结论,文章分别记录下不同阵元数目下TOPS算法、TOFS算法以及本文改进算法的运算时间,仿真条件与实验1相同,波束数固定取为5。算法的处理平台为Windows XP系统、双核2.8 GB CPU、2 GB内存,采用Matlab2010进行算法仿真,4种算法的运算时间如表1所示。由表中可以看出,改进后的TOFS算法运算时间比常规的TOFS算法时间稍长,这是因为算法加入了共轭重构的过程,而将改进后的算法从阵元空间变换到波束空间中之后,算法的运算时间大大缩短,尤其是在阵元数目比较多的时候,优势更为明显。但随着阵元数目的逐渐降低,这种优势也越来越小,当阵元数目为10时,算法在阵元空间和波束空间中的计算时间基本相同。需要说明的是,随着阵元数的减少,算法需要的波束数也随之降低,以10阵元数为例,波束数为3即可满足算法需求。因此,本文提出的在波束域中改进的TOFS算法能够有效提高DOA估计效率。

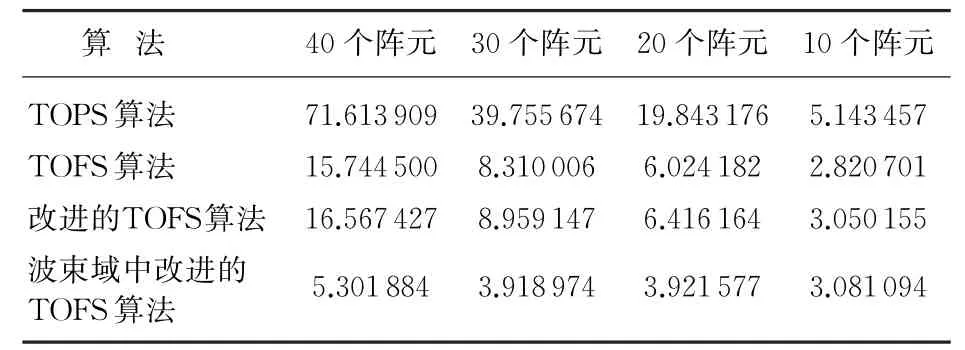
表1 4种算法的运算时间s

5 结束语

本文将矩阵重构方法和TOFS算法相结合,提出了一种改进的TOFS算法,新方法解决了原算法不能处理相干信号的问题,并且一定程度上提高了原算法的测向精度。再将改进后的算法运用到波束空间中后,大大降低了运算量,虽然对算法精度有一定影响,但相比于运算量降低的优势,该影响处于可接受范围之内。与阵元域的TOFS算法相比,应用于波束域的改进TOFS算法的协方差矩阵维数明显减小,因而对于大阵元数目、小信源数目的应用场合,计算复杂度将明显降低,因而更适于工程应用。

[1]林波,张增辉,朱炬波.基于压缩感知的DOA估计稀疏化模型与性能分析[J].电子与信息学报,2014,36(3):589-595.

[2]YAN F G,JIN M,QIAO X L.Source Localization Based on Symmetrical MUSIC and Its Statistical Performance Analysis[J].Science China Information Sciences,2013,56(6):1-13.

[3]蒋柏峰,吕晓德,向茂生.一种基于阵列接收信号重排的单快拍DOA估计方法[J].电子与信息学报,2014,36(6):1334-1339.

[4]SCHMIDT R O.Multiple Emitter Location and Signal Parameter Estimation[J].IEEE Trans on Antennas and Propagation,1986,34(3):276-280.

[5]ZHUANG Jie,LI Wei,MANIKAS A.An IDFTBased Root-MUSIC for Arbitrary Arrays[C]∥2010 IEEE International Conference on Acoustics,Speech and Signal Processing,Dallas,Texas,USA:IEEE,2010:2614-2617.

[6]XU X,YE Z,PENG J.Method of Direction-of-Arrival Estimation for Uncorrelated,Partially Correlated and Coherent Sources[J].IET Microwaves,Antennas&Propagation,2007,1(4):949-954.

[7]曾浩,朱自华,李慧君,等.均匀圆阵下的宽带信号DOA估计算法[J].电路与系统学报,2013,18(1):432-436.

[8]景小荣,杨洋,张祖凡,等.均匀线阵混合信源DOA估计与互耦误差自校正[J].系统工程与电子技术,2014,36(9):1696-1702.

[9]闫杰.宽带相干信号DOA估计算法研究[D].重庆:重庆邮电大学,2013.

[10]YOON Y S,KAPLAN L M,McCLELLAN J H.TOPS:New DOA Estimator for Wideband Signals[J].IEEE Trans on Signal Processing,2006,54(6):1977-1989.

[11]李焜,方世良.基于波束域的子空间正交性测试宽带DOA估计方法研究[J].信号处理,2012,28(1):131-138.

[12]YU H Q,HUANG Z T,LIU J,et al.TOFS:A New DOA Estimator for Wideband Sources[J].Journal of Astronautics,2007,28(5):1304-1308.

[13]荣佶,吴永晶,郭艺夺.波束空间的双基地MIMO雷达定位方法[J].雷达科学与技术,2014,12(4):411-416,422.RONG Ji,WU Yong-jing,GUO Yi-duo.Target Localization Method Based on Beamspace for Bistatic MIMO Radar[J].Radar Science and Technology,2014,12(4):411-416,422.(in Chinese)

[14]FENG J,SUN C,TANG J S,et al.Beamspace DOA Estimation Algorithms with Robustness Against Signal Steering Vector Errors and Interference Nonstationarity[J].Technical Acoustics,2006,25(6):617-622.