局域零相关多相码设计∗

刘志国,王亚利

(1.中国电子科技集团公司第二十研究所,陕西西安710068;2.空军工程大学理学院,陕西西安710051)

0 引言

对于MIMO雷达而言,正交波形是一种理想的波形。而实际上,完全正交且相关函数旁瓣为零的信号是不存在的,因此在正交波形设计中,主要任务是使发射波形具有好的自相关和互相关性质,这也是一些实际应用中必需的,例如在距离压缩的应用中。在这种情况下,波形具有好的相关性不仅强调两两信号之间的互相关性要很弱,还隐含了信号本身具有很低的自相关旁瓣,即信号自身是高主副比的脉冲压缩信号。上述好的相关性确保了在接收端匹配滤波能够提取出感兴趣距离单元中的后向散射信号,而抑制其他距离单元中的后向散射信号。另外,实际的硬件(功率放大器和A/D转换器)实现要求发射波形是恒模的。

到目前,已经有大量关于MIMO雷达波形设计的文献。文献[1-2]通过优化发射波形的相关矩阵来获得期望发射波束方向图,而文献[3]直接设计波形来逼近期望的相关矩阵。文献[4-6]假设某些先验信息已知(例如,目标脉冲响应),然后通过设计波形来优化某个统计指标(例如,目标脉冲响应和反射信号间的互信息)。文献[7-8]设计正交波形以期获得好的自相关和互相关性质,文献[9]的目标是降低MIMO雷达模糊函数的旁瓣(即同时考虑距离和Doppler分辨率)。文献[10]提出了几种恒模MIMO雷达波形设计的循环算法,目的也是获取好的相关性质,由于对相位未加约束,设计所得序列的相位是-π到π中的任意值,因此需要数量化。

当设计方法考虑波形所有的自相关旁瓣和互相关时,其旁瓣峰值经常出现在自相关主瓣附近。在某些实际应用中,例如在SAR成像时,发射脉冲相对较长,以至于近距离单元和远距离单元的后向散射信号重叠。在这种情况下,仅仅0附近延迟单元的相关性与距离分辨率有关。再比如空中目标通常是稀疏分布的,因此可以假设感兴趣目标附近没有其他目标。因此,发射波形仅需要在0延迟单元附近具有较低的自相关旁瓣和互相关,而对远离主瓣区域的旁瓣峰值可以不作限制。

1 波形设计准则

假设一个MIMO雷达系统具有M个发射天线,每个天线发射一个由L个子脉冲组成的相位编码脉冲,这个脉冲信号[11]可以表示为

式中,

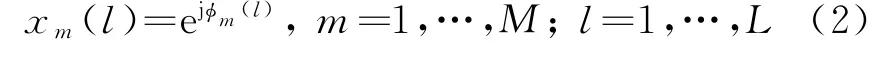
是所要设计的相位编码;p(t)定义为

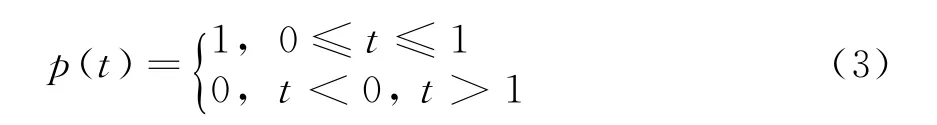
tb为子脉冲脉宽;T=Ltb为整个脉冲的脉宽。波形设计的主要目的就是要使离散波形集合满足期望的相关性质。这里首先要指出的是,当设计连续相位编码时,ϕm(l)∈[0,2π],即ϕm(l)可以是0和2π间的任意值;当设计离散相位编码时,假设多相码的相位数是J,也就是说发射信号的相位不能是任意的,而必须是在J个离散相位中选取,则ϕm(l)应满足如下约束:

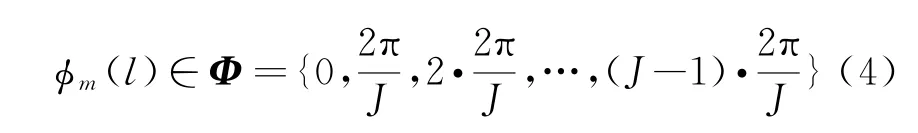
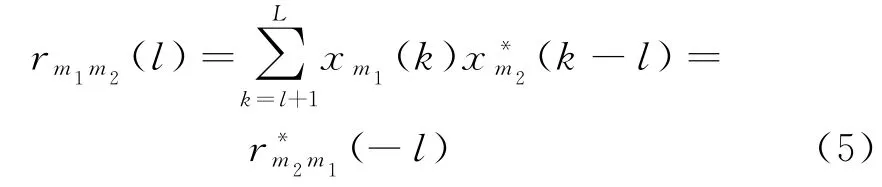
式中,m1,m2=1,…,M,l=0,…,L-1。当m1=m2时,式(5)表示的非周期自相关函数。当多相码信号的相位是离散时,式(5)可以改写为

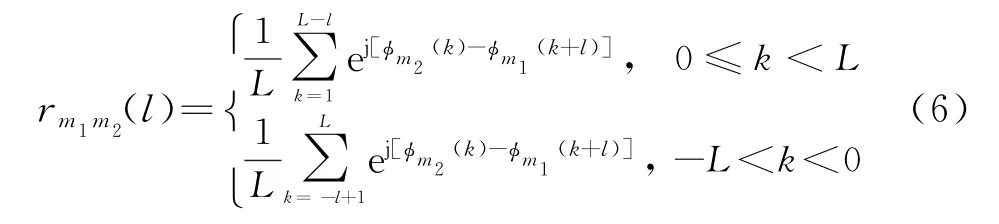
非周期自相关函数可以表示为

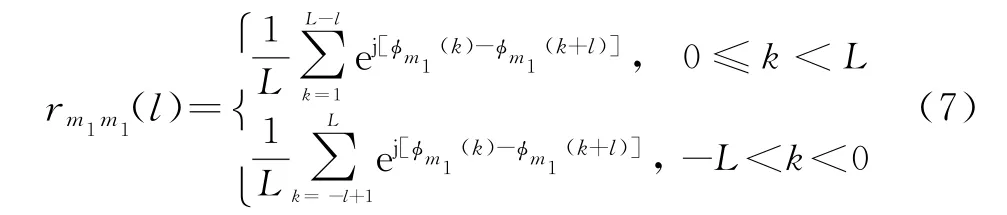
理想情况下,正交信号自相关函数应该满足Dirac函数的形式,而互相关则应为零,即

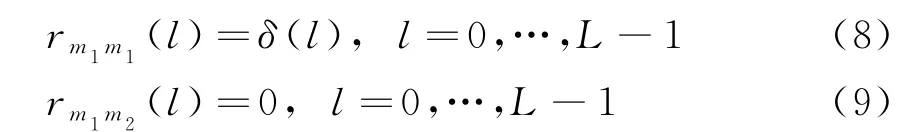
事实上,上述条件式(8)和式(9)是无法满足的。因此已有的设计方法[7-8]都是以某种准则来设计正交波形,以达到降低自相关旁瓣和互相关的目的。为了使得所设计的MIMO雷达波形具有理想的相关性质,可以定义如下的目标函数:

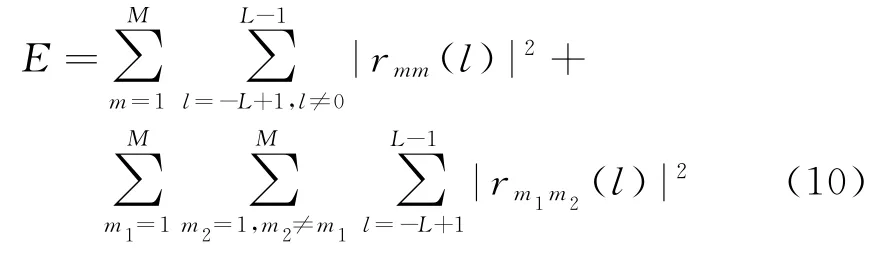
式(10)定义的目标函数和文献[7-8]中的目标函数都是考虑整体降低所有的自相关旁瓣和互相关。文献[3,10,12]基于实际需要提出尽可能地降低主瓣附近若干单元的自相关旁瓣和互相关,而不考虑远离主瓣的自相关旁瓣和互相关峰值。因此目标函数可以表示为

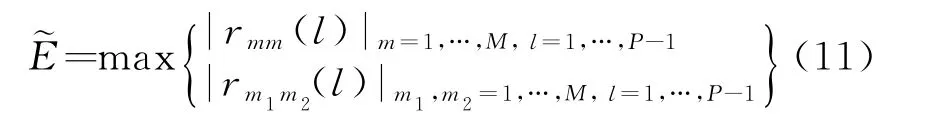
或

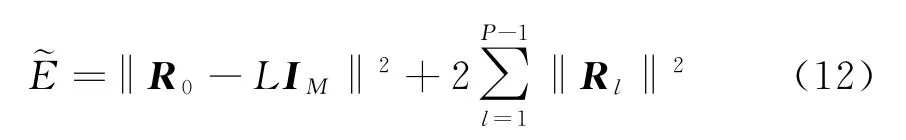
式中,P-1为感兴趣的最大延迟,

具体而言,(P-1)tb应该不小于临近距离单元和远距离单元后向散射信号的最大往返延迟。

式(11)和式(12)都是非凸问题,没有优化工具箱能直接给出最优解,因此对式(11),学者们提出利用模拟退火算法或遗传算法来求解。而对式(12),当ϕm(l)是连续相位时,文献[10]提出了CAN(CA-New)和改进算法WeCAN(Weighted-CAN),CAD(CA-Direct)等。当然不同的算法对目标函数进行了不同的变化,WeCAN使用的目标函数为

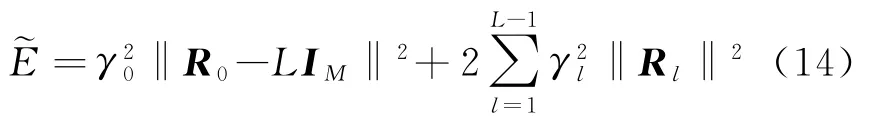
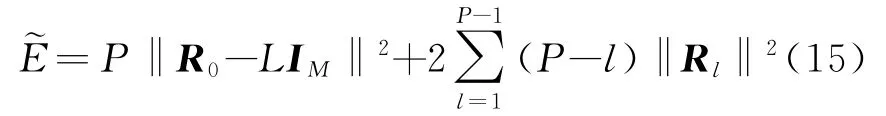
对于感兴趣单元(零相关区域,ZCZ)长度P的取值,遗传算法并没有给出具体的要求,但是很显然P受脉冲信号个数M和长度L的制约。如果P选择过大,算法并不能给出好的结果,而且随着P的增大,感兴趣单元内的自相关旁瓣峰值和互相关峰值都会增加。对于P的取值问题,文献[10]指出只有当P≤(L+M)/2M时,才可能设计出波形使得式(12)趋于零。例如当L=256,M=4时,只有选择P≤32才有可能获得理想波形。

2 设计结果

2.1 遗传算法

假设MIMO雷达系统有3个发射天线,每个天线发射长度为128的四相编码脉冲,,P=20。遗传算法的初始种群规模为100,交叉概率为0.9,变异概率为0.05。设计所得波形零相关区域内自相关和互相关特性如表1所示。表中对角元是所设计波形在零相关区域内归一化自相关旁瓣峰值,非对角元是不同脉冲信号间的归一化互相关峰值。平均自相关旁瓣峰值是0.102 9 dB或-19.751 7 dB,平均互相关峰值是0.1096 dB或-19.2038 d B。脉冲信号1,2,3的自相关函数图像如图1(a)、(b)、(c)所示。脉冲信号1和2,1和3,2和3间的互相关函数如图1(d)、(e)、(f)所示。

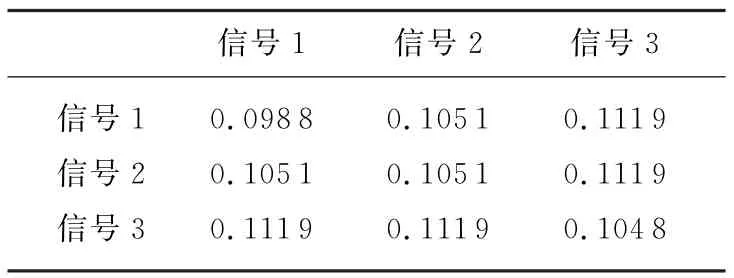
表1 ZCZ内自相关旁瓣峰值和互相关峰值(遗传算法)

图1 自相关函数和互相关函数(遗传算法)

2.2 循环算法

令M=3,L=128,P=20,利用循环算法进行波形设计。所得波形的自相关函数与互相关函数特性如图2所示。表2给出了循环算法得到的波形零相关区域内的自相关旁瓣峰值和互相关水平。对比表1和表2不难看出,循环算法所得的波形在感兴趣区域具有更理想的性质。这得益于循环算法没有对相位的个数进行约束,而当波形所包含的脉冲信号个数和长度相同时,相位个数的增加会更有利于得到更低的旁瓣水平和互相关水平。由于不约束相位个数相当于相位个数是无穷多,因此循环算法得到更好的结果就不难理解了。

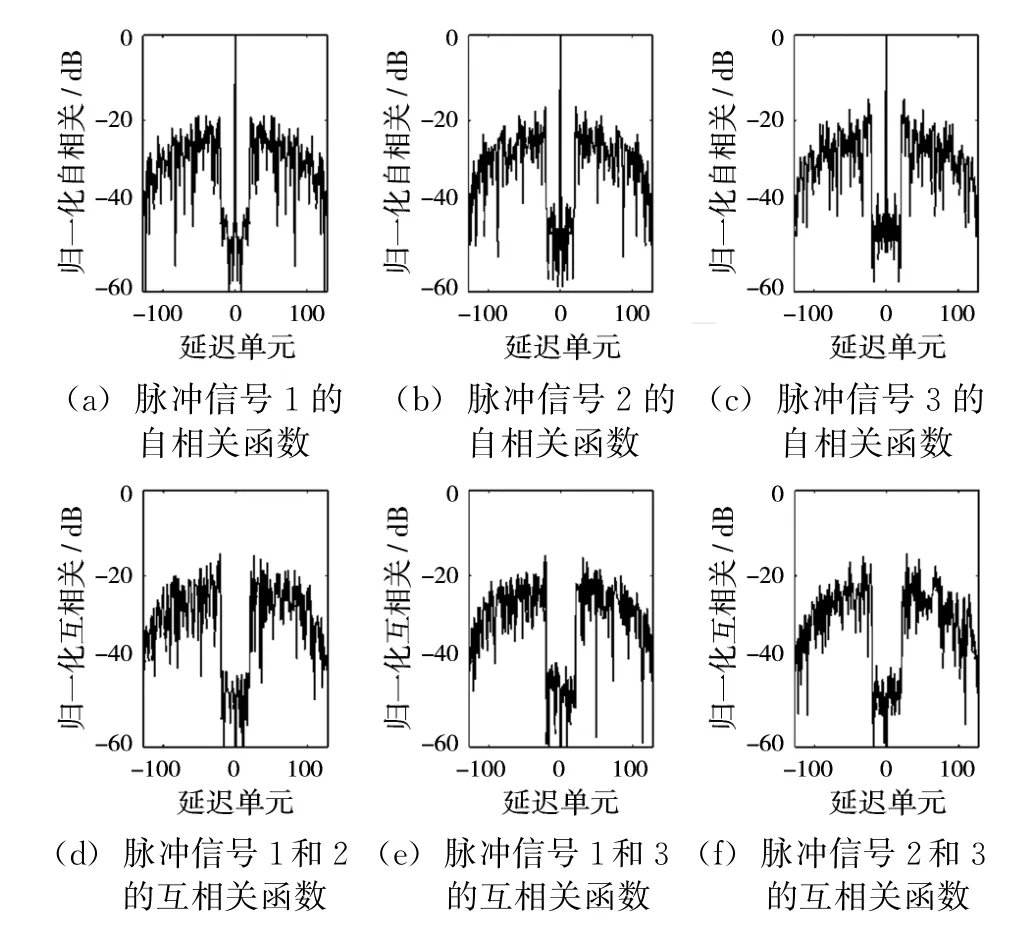
图2 自相关函数和互相关函数(循环算法)

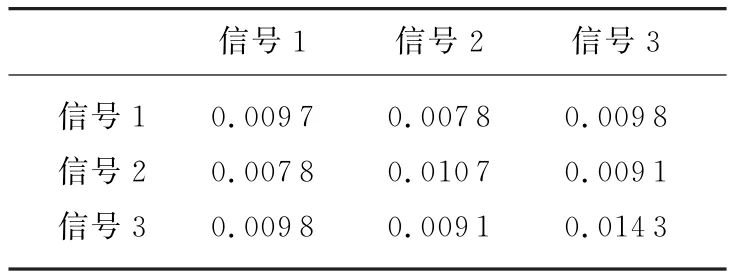
表2 ZCZ内自相关旁瓣峰值和互相关峰值(循环算法)

3 结束语

针对一些实际应用,介绍了基于遗传算法和循环计算的正交多相码的优化设计方法,这些方法可以有效降低自相关主瓣附近若干距离单元内(称为零相关区域)自相关旁瓣和互相关。遗传算法可以设计在一定准则下最优的多相码,但是计算复杂度较大,需要较长的优化时间。在可以离线设计的雷达应用中,可以利用基于遗传算法的方法进行波形优化。利用循环算法设计类零相关信号,此方法计算量小,在自相关主瓣附近若干距离单元内自相关旁瓣和互相关具有非常优异的表现。

[1]CUI G L,LI H B,RANGASWAMY M.MIMO Radar Waveform Design with Constant Modulus and Similarity Constraints[J].IEEE Trans on Signal Processing,2014,62(2):343-353.

[2]FUHRMANN D R,SAN ANTONIO G.Transmit Beamforming for MIMO Radar Systems Using Signal Cross-Correlation[J].IEEE Trans on Aerospace and Electronic Systems,2008,44(1):171-186.

[3]STOICA P,LI J,ZHU X M.Waveform Synthesis for Diversity-Based Transmit Beampattern Design[J].IEEE Trans on Signal Processing,2008,56(6):2593-2598.

[4]YANG Y,BLUM R S.MIMO Radar Waveform Design Based on Mutual Information and Minimum Mean-Square Error Estimation[J].IEEE Trans on Aerospace and Electronic Systems,2007,43(1):330-343.

[5]NIJSURE Y,CHEN Y,YUEN C.et al.Adaptive Distributed MIMO Radar Waveform Optimization Based on Mutual Information[J].IEEE Trans on Aerospace and Electronic Systems,2013,49(2):1374-1385.

[6]AHMED S,ALOUINI M S.MIMO Radar Waveform Covariance Matrix for High SINR and Low Side-Lobe Levels[J].IEEE Trans on Signal Processing,2014,62(8):2056-2065.

[7]应斌,严济鸿,何子述.MIMO雷达相位编码波形设计与实现[J].雷达科学与技术,2013,11(5):511-515.YING Bin,YAN Ji-hong,HE Zi-shu.Phase Encoding Waveform Design and Implementation for MIMO Radar[J].Radar Science and Technology,2013,11(5):511-515.(in Chinese)

[8]DENG H.Polyphase Code Design for Orthogonal Netted Radar Systems[J].IEEE Trans on Signal Processing,2004,52(11):3126-3135.

[9]TANG B,TANG J,PENG Y N.Waveform Optimization for MIMO Radar in Colored Noise:Further Results for Estimation-Oriented Criteria[J].IEEE Trans on Signal Processing,2012,60(3):1517-1522.

[10]HE H,STOICA P,LI J.Designing Unimodular Sequence Sets with Good Correlations-Including an Application to MIMO Radar[J].IEEE Trans on Signal Processing,2009,57(11):4391-4405.

[11]MELVIN W L,SCHEER J A.Principles of Modern Radar[M].Croydon:SciTech Publishing,2012.

[12]金明,廖桂生,李军.基于遗传算法的类零相关多相码设计[J].系统工程与电子技术,2010,32(1):14-17.

JIN Ming,LIAO Guisheng,LI Jun.Zero Correlation Zone Like Polyphase Code Design Based on Genetic Algorithm[J].Systems Engineering and Electronics,2010,32(1):14-17.(in Chinese)