一种基于UKF交互多模型算法∗

(中国电子科技集团公司第二十研究所,陕西西安710068)

0 引言

随着舰载防空导弹技术的发展,现代反舰导弹在距离目标舰艇30 km以内时,普遍采用机动的方式降低舰载防空系统的跟踪精度与命中概率[1]。反舰导弹在中段距离目标20 km左右,一般采用蛇形机动等方式规避舰空导弹,有的反舰导弹除了蛇形机动外还采用降高或在极短时间内将速度由亚音速迅速加速到2.5～3 Ma的超音速的方式来规避舰载防空导弹的打击;在末段10 km以内,一般采用爬升俯冲或继续降高飞行的方式规避防空武器的打击,这对现代舰载防空武器与探测跟踪系统提出了较高的要求。为了应对反舰导弹的中端机动等问题,需要对机动目标跟踪算法改进。典型的目标跟踪滤波器都是单模型的,因此只能对具有单一运动状态的目标有较好的跟踪性能。但是实际的目标运动经常由多种运动状态组合而成,因此单一模型的滤波器对机动目标的跟踪性能都不是太好。目前比较成熟且效果较好的目标跟踪算法是交互多模型(IMM)算法[2]。IMM算法是一种基于混合系统状态估计的次优算法。在k时刻利用交互多模型算法时,认为每一个模型滤波器都有可能成为当前有效的系统模型滤波器,每一个滤波器的初始值都是基于前一个时刻所有模型滤波结构的合成。最后的滤波结果是每一个滤波器的综合输出。

但是,交互多模型算法的性能与模型集的选取与单模型的跟踪性能有很大关系。本文以基于匀速运动、匀加速运动、匀速转弯和“当前”统计模型这四种跟踪模型组成的模型集为基础,对交互多模型算法进行了仿真研究。为了在高机动目标条件下获得较高的跟踪精度,将无味滤波算法(UKF)应用到了IMM算法中,并通过仿真对UKF-IMM算法进行了仿真验证。

1 基于无味滤波的交互多模型算法

1.1 交互多模型算法

IMM算法是一种基于软切换的多模型算法,在该算法中存在多个目标运动模型,每个运动模型对应于不同的目标机动输入水平。在计算出模型为正确的后验概率之后,就可以通过对各模型正确的状态估计加权求和来给出最终的目标运动状态估计。这里加权因子为模型正确的后验概率。交互多模型的具体步骤[3]如下:

1)计算目标在k时刻的预测位置

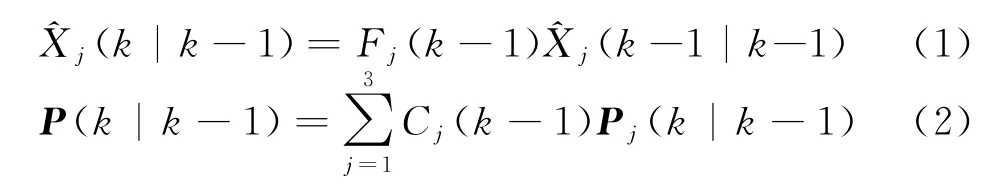
F为状态转移矩阵,C为权系数。

2)相互作用

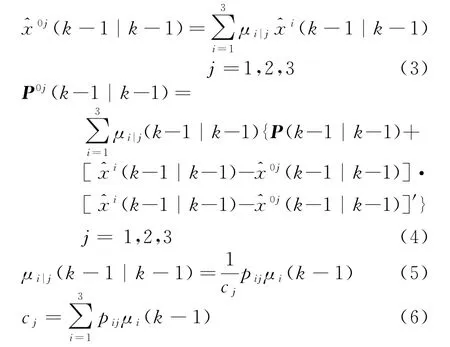
式中,pij为模型开关概率,通常认为其服从马尔可夫过程,μi为模型转换概率。

3)滤波

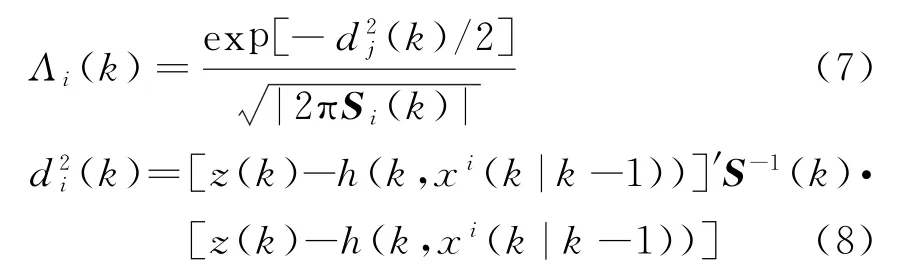
式中,S为滤波量测预测协方差矩阵,z,h分别为量测输入和量测预测值。

4)模型概率更新

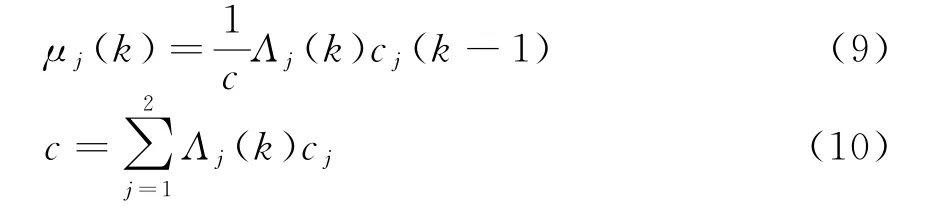
5)形成综合输出

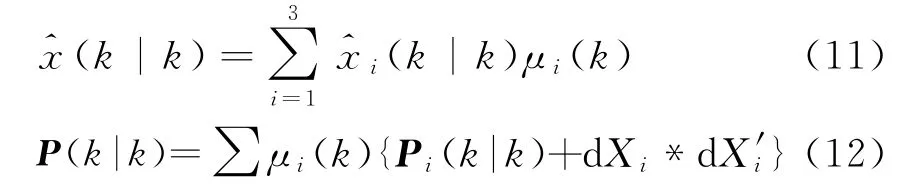
其中,

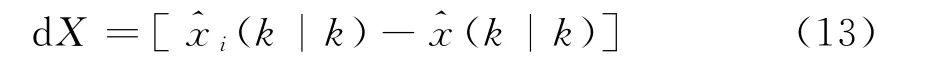
1.2 模型集的选取

考虑到目标常见的运动方式有匀速、匀加速和匀速转弯三种,因此在确定模型集时首先加入以上三种模型。另外,为了在目标运动状态发生突变时滤波器可以快速跟上运送状态的突变,在模型集内加入了“当前统计模型”。具体的模型[4]为匀速运动模型、匀加速运动模型、匀速转弯模型和“当前”统计模型。

1.3 UKF算法

无味滤波算法(UKF)是一种基于Unscented变换的非线性状态估计算法,Unscented变换是一种近似计算,建立了非线性变换的随机变量的统计特性的新方法,它建立的依据是:近似一个概率分布比近似一个任意的非线性变换(或函数)要容易[4]。UKF算法相比EKF算法能精确估计任意非线性函数的二阶泰勒近似解;估计误差为三阶及三阶以上高阶矩项截断误差。无味滤波算法具体步骤见文献[5]。

2 仿真验证

2.1 仿真场景

仿真场景如下:雷达为三坐标搜索雷达,数据更新周期为2 s;距离测量精度为150 m;方位与俯仰角测量精度为0.3°。目标轨迹的仿真采用典型反舰导弹对舰艇的攻击过程弹道,具体目标的运动仿真参数如表1所示,目标的轨迹如图1所示。

表1 目标轨迹仿真参数

图1 目标运动轨迹曲线

2.2 仿真结果

为了比较采用交互多模型算法的效果,对基于扩展卡尔曼滤波算法的交互多模型(EKFIMM)与基于无味滤波的交互多模型算法(UKFIMM)进行比较。经过100次蒙特卡罗仿真,得到EKF-IMM和UKF-IMM的仿真结果如表2所示。

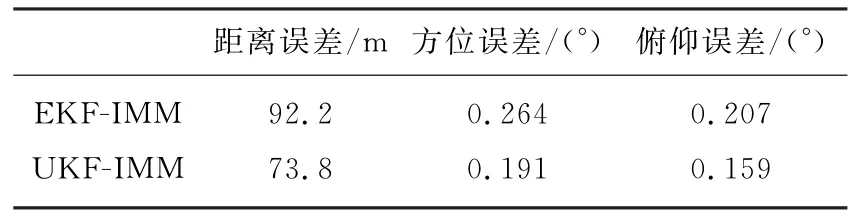
表2 仿真结果对比

由表2中数据可以看出,采用UKF-IMM算法可以显著地提高对高机动目标的跟踪精度。采用UKF-IMM和EKF-IMM算法对雷达测量和目标跟踪在距离、方位、俯仰的误差进行仿真,仿真结果分别如图2和图3所示。由仿真结果可以看出,在目标蛇形机动段,采用EKF-IMM算法在方位上会出现跟踪滞后,方位误差曲线出现震荡,而采用UKF-IMM算法稳态性能较好。

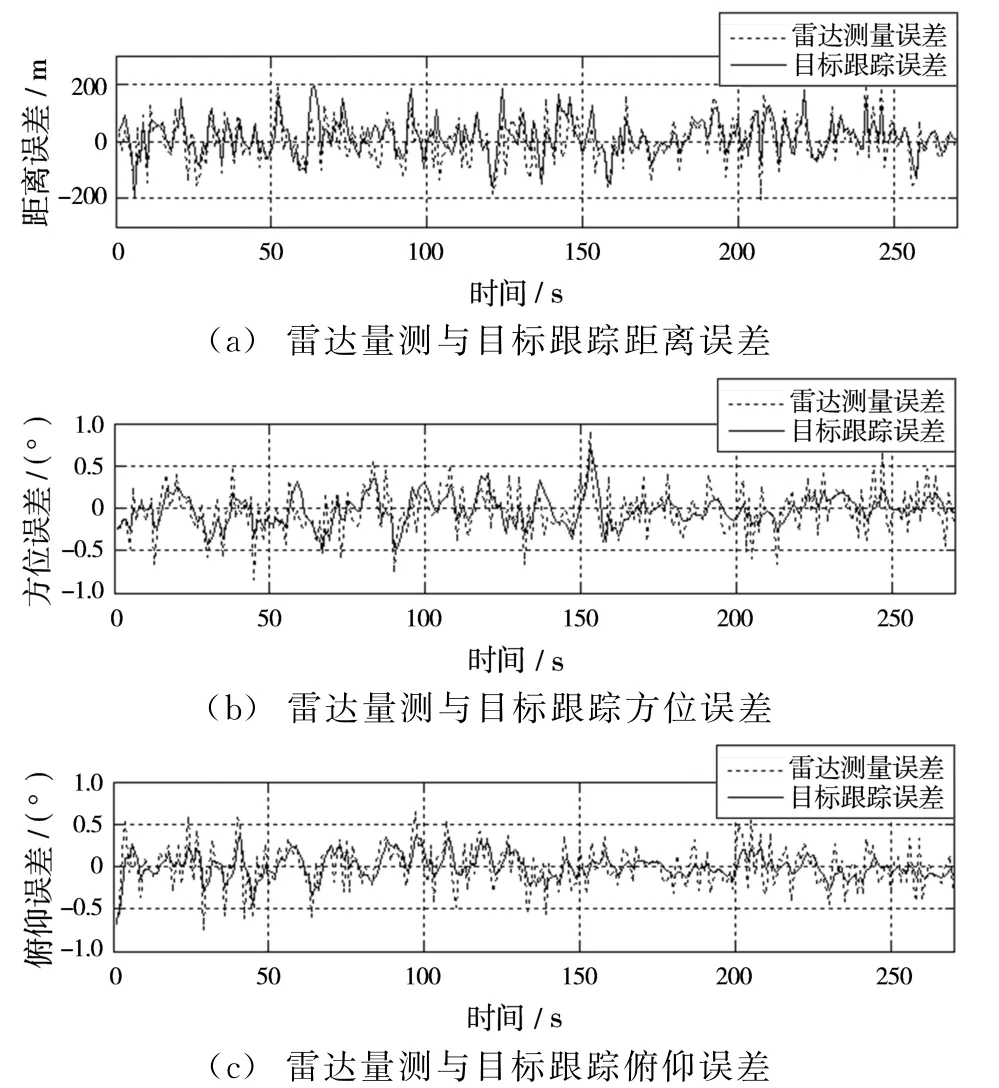
图2 UKF-IMM仿真结果

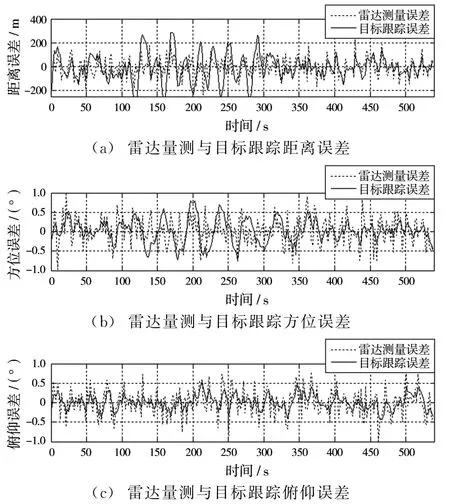
图3 EKF-IMM仿真结果

3 结束语

针对实际运动中目标运动的复杂多变,单模型的目标跟踪滤波器无法跟踪的问题,提出一种基于UKF交互多模型算法。经仿真验证,与EKF-IMM算法相比,UKF-IMM算法的跟踪性能更优,可以显著地提高对高机动目标的跟踪精度。该算法的有效性在实际的陆地与海上雷达组网试验中也得到了验证。

[1]张峰,田康生,息木林.弹道导弹运动建模与跟踪研究[J].弹箭与制导学报,2012,32(3):53-58.

[2]张华睿,杨宏文,郁文贤.多目标跟踪时的雷达波形调度问题[J].雷达科学与技术,2012,10(6):650-655.ZHANG Hua-rui,YANG Hong-wen,YU Wen-xian.Optimal Waveform Scheduling for Multi-Target Tracking[J].Radar Science and Technology,2012,10(6):650-655.(in Chinese)

[3]BLOM H A P,BAR-SHALOM Y.The Interacting Multiple Model Algorithm for Systems with Markovian Switching Coefficients[J].IEEE Trans on Automatic Control,1988,33(8):780-783.

[4]周猛飞,肖成松,逯振飞,等.基于UKF的滚动时域估计方法研究[J].计算机与应用化学,2013,30(12):1406-1410.

[5]LI X R,JILKOV V P.Survey of Maneuvering Target Tracking Part I:Dynamic Models[J].IEEE Trans on Aerospace and Electronic Systems,2003,39(4):1333-1364.