基于Hermite插值的时变信号谐波测量研究

吴超凡，陈隆道

(浙江大学电气工程学院，浙江杭州310027)

0 引言

准确的谐波分析是对电网进行有效控制和保护的前提，FFT 算法因为能快速地分析谐波参数而在电力系统的数字信号处理技术中被广泛使用，在同步采样的前提下，能够满足工程上实时测量的要求。但是当信号频率发生偏移时，应用传统的FFT 直接对电网信号进行检测时，将造成一定的误差。这是因为均匀采样频率和信号周期之间不再存在整数倍关系时，所截取的数据长度也不再是严格的整数倍信号周期。此时若直接对采样序列用FFT 算法来分析谐波将会发生比较严重的频谱泄漏现象，频谱和其他相关电参量的测量结果也随之存在很大的误差。此外，还有一种更为恶劣的情况，即待测信号是基波频率不断变化的非稳态周期信号，由于信号频率不仅仅发生了偏移，还处在振荡之中，这对谐波测量的实时性有很高的要求。以微网为例，随着化石燃料等常规资源的日渐枯竭以及人们对环境污染问题的进一步关注，环保、高效、灵活的微网成为了电力系统未来的一大发展方向［1-2］。但是当微网处于孤岛运行时，因为内部发电和负荷以及储能元件的不平衡和电力电子器件等非线性元件的大量使用，微网内部的谐波信号往往是实时变化的，具有随机性、分布性、非平稳性等特点，对其的控制和保护带来了很大的困难。因此，寻找一种能够准确测量一般电力网络信号且适用于微网等时变信号测量的谐波测量方法是很有必要的。

一般来说，当电力系统频率发生变化时，需要保证采样频率和系统频率的同步。应用于FFT 方法的同步技术大致可以分为两类—重采样和插值。对于重采样法，第一步在于测量电力系统的基频，然后根据测量结果控制模数转换器(ADC)来对信号进行重新采样。为了保证频率同步，可以应用过零检测、频域插值法、线性调制Z 变换、牛顿法、锁相环(PLL)等技术来防止谱泄漏［3-8］。

当频率失去同步时，可以应用一些窗函数来减少谱泄漏，譬如Hanning 窗、Hamming 窗、Blackman 窗等。然而，这类技术在谐波分析中通常只能减少计算误差［9-11］。而参数估计的方法是在非同步情况下的另外一种解决方案，和基于FFT 的方法对比，该方法往往拥有更高的频率分辨率。

对于另一类应用于同步化的方法—插值法，其原理为先计算出信号的基波频率进而得到同步化的采样频率。然而该频率并不一定能够灵活适用于一些低成本的ADC，在这种情况下，采样数据将基于同步化的理想采样频率进行插值重组。在该过程中，要用到一些插值算法，例如牛顿法、多项式法、多次样条法等［12］。应用插值法时不会发生失去同步的情况，但会引入额外的计算量。

本研究主要讨论基于傅里叶变换的谐波计算方法，而非同步采样信号的同步化是FFT 算法能够对信号频谱进行高精度分析的有力保障，通过信号的同步化，可以使得频率分辨率和信号的谐波分布取得一致，能尽可能地减小频谱泄漏等问题带来的误差。对于重采样法，需要先测量电力系统的基频，再根据测量结果对采样部分进行反馈控制以调整采样频率重新进行采样。但是若待测信号是一个时变信号时，其基波频率一直处于变化之中，该方法很难实现对基波频率的实时跟踪，一旦失去同步，还是会受到谱泄漏等问题的影响。

所以本研究采用插值以重构采样数据的方法，即通过对采样序列的插值或自适应算法，实现采样数据的重构，使得重新得到的数据逼近理想化，再进行参量的运算和分析。这种方法可以适用于一些低成本的ADC，且不会发生失去同步的情况，适用于时变信号的同步化。

本研究将在其基础上采用Hermite 插值的方法对非同步采样序列进行同步化处理，并用变频率信号进行仿真计算以验证其可行性。

1 非同步数据的重定位

对于非同步数据的同步化，首要的工作应该是确定信号的周期［13］。因为周期信号的数字化处理存在一定的延迟以及电网实际频率的偏移所产生的非同步，文献［14］对于不含直流分量的周期信号采取信号过零检测的方法来确定其周期，一般情况下，信号周期的计算分为中间部分的若干个完整采样周期和首尾的小数部分，即:

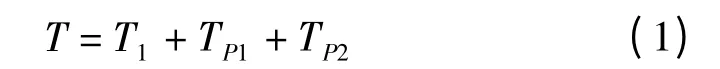
式中:T1—一个信号周期中间的整数个采样周期部分，可以依据两个相同特征的过零点之间的采样点数来计算得到;TP1，TP2—信号始端和尾端的周期小数部分，可以通过对过零点附近的采样点进行插值来逼近信号在采样点附近的函数值，然后通过解函数方程来计算得到该小数部分。

一个含有最高谐波次数为30 次的周期信号，在过零点附近用一阶线性方程插值计算其周期，误差在0.009%以内［15］，足以满足一般工程上的精度需求。

设x1(k)是包含一个完整信号周期的非同步采样序列，在计算出信号周期T 之后，便可以由T 得到理想的同步采样周期Tsi，为了后续FFT 的方便，一般将T 除以2 的幂次方。因此，理想同步序列x2(i)中的第i 个同步采样点在实际采样序列中的下标为:

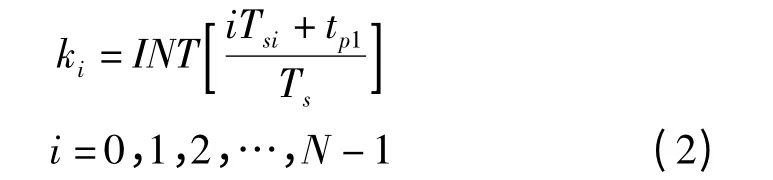
式中:INT［］—取整算子，Tsi—理想同步采样周期，Ts—实际采样周期，tp1—实际采样序列和同步采样序列始端的时间差。在计算得到下标ki后，就能够根据ki和ki+1 点的实际采样值来构造插值函数得到同步化处理后的理想序列。

2 Hermite 插值同步化算法

本研究提出一种基于Hermite 算法的插值同步化算法，因为实际电网中的信号波形大致上近似于三角函数，其二阶导数大致上也和三角函数一样呈周期变化。在信号的过零点附近往往其斜率变化率不大，用线性插值便有足够高的精确度;而在信号的波峰和波谷附近，信号的二阶导数在一般情况下也到达极值，在图像上看，这段信号也拥有较大的曲率，此时若用线性插值算法则不大妥当，会产生很大的误差，故本研究考虑采取Hermite 插值算法来对信号进行拟合。

已知两节点三次Hermite 插值公式如下:

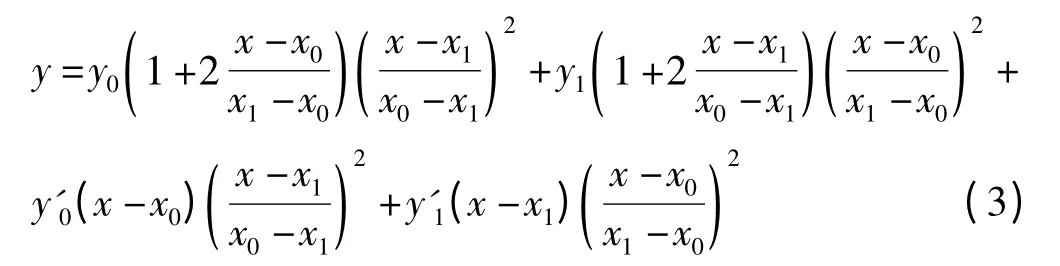
在计算得到ki后，由ki和ki+1 点的函数值和一阶导数值代入式(3)并化简后可得构造两点的Hermite 插值函数如下:

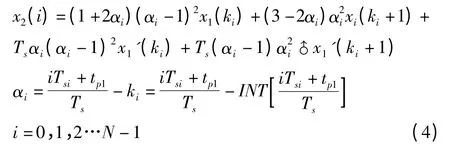
式中:x'1()—x1()的一阶导数，可以用插值点前后的采样值差商运算近似求得:

x'1(ki+1)同理，将式(5)代入式(4)就是对于采样序列的Hermite 插值同步化公式。再对该算法的误差进行分析，设同步化的取样点ti处于实际采样序列的点tki和点tki+1之间，则在ti点上有理论截断误差为:

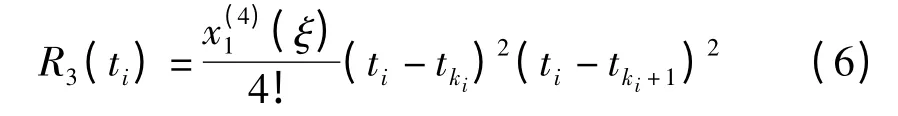
式中:ξ—tki和tki+1之间的某值，实际上由于tki和tki+1充分接近，以至于在区间内单调，可以用(tki)和中的较大者来代替来得到在

ti点上最大的理论截断误差:

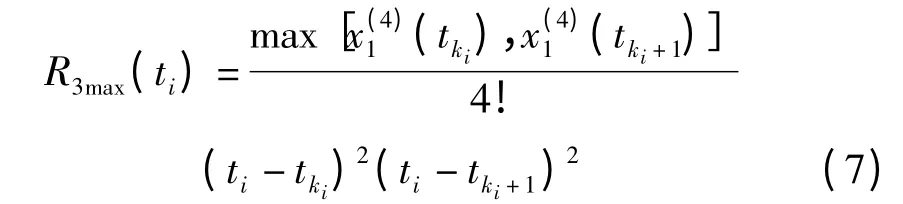
值得一提的是，抛物线插值算法的截断误差为:

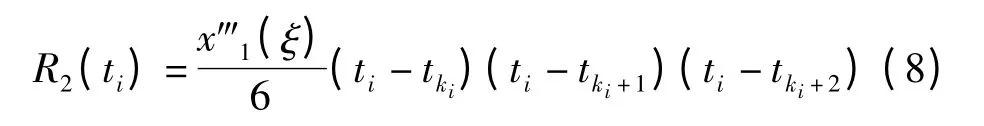
通过对比式(6)和式(8)不难发现，Hermite 插值的截断误差比抛物线插值的误差拥有更高的阶数，所以R3较之R2要更小，即在采样序列采用Hermite 插值可以提高插值的精度。

3 仿真实验

3.1 固定频率信号仿真

考虑到电网中的实际信号的谐波成分多为奇次谐波，同时出于方便观察的目的对谐波幅值进行设定，有一信号如下:

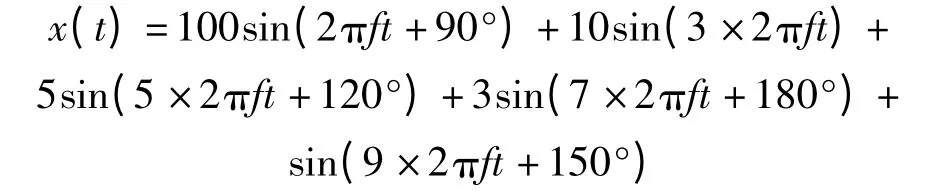
式中:f—电网的基波的实际频率，取f 为49.5 Hz，49.7 Hz，50 Hz，50.3 Hz，50.5 Hz 作为频率测试点。在仿真计算时，本研究取采样频率为6 400 Hz，为保证选取的信号至少包含一个完整周期，共取256 个采样点。

本研究通过对该函数进行采样后得到x1(k)，通过Hermite 插值同步化算法处理后得到x2(i)后再对其进行FFT 变换计算谐波幅值，结果如表1所示。

表1 同步化后的幅值仿真结果

由仿真结果可知，在49.5 Hz ～50.5 Hz 的电网基波范围内，该同步化算法在小于等于9 次以下的谐波幅值有较高的精度，其相对误差都在0.08%以内，且伴随着谐波次数增加其相对误差并没有明显的增加。

可见该算法在处理一般的非时变的频偏信号时已有足够高的精度，完全可以适用于一般情况下的电网谐波分析。

3.2 变频率信号仿真

由于负荷和发电量处于动态的平衡状态，微网中的实际信号的基频并不是一成不变的，供需关系的实时变化带动着基波频率的变化。除了微网中的谐波信号以外，还存在快速变动的过程信号等非稳态周期信号，其特征即为基波频率在一定范围内快速波动，只有单周期的测量结果才有实际意义，在这种前提下，对算法的实时性有了较高的要求，且要求对单个周期的采样信号即可进行计算。基于FFT 的重构法仅需一个完整采样周期即可完成数据的二次同步，能够适用于这种特殊场合。为了更好地对该类信号进行仿真，本研究将构造一个频率偏移实时变动的信号对分段插值同步算法进行验证:

式中:f=50 ×［1 +0.01sin(2π ×5t)］。为了便于计算，用一正弦变化的频率来模拟非稳态周期信号中实时变化的频率，其变化范围在49.5 Hz ～50.5 Hz 之间，变化的周期为0.2 s。

在采样频率为6 400 Hz，256 个采样点的前提下对信号进行取样后，分别用线性插值算法、抛物线插值算法、Hermite 插值算法对其进行同步化并FFT 后结果如表2所示。

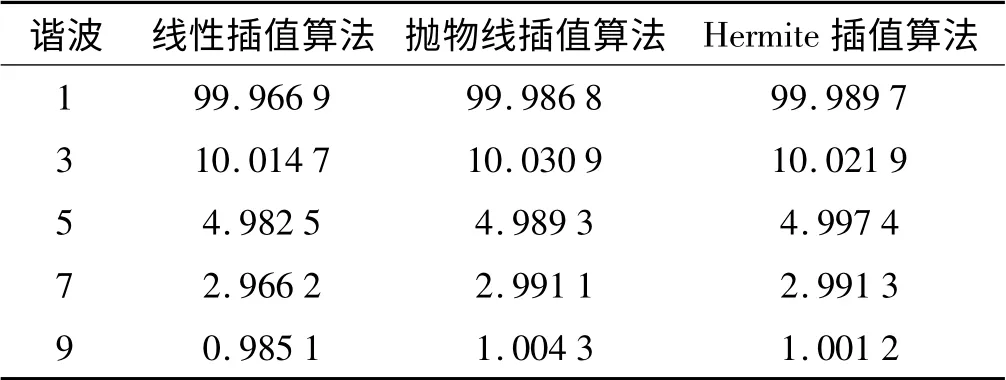
表2 变频信号的仿真结果

4 结果分析

由仿真结果可以看出，当用变频率信号对3 种不同的插值算法进行验算时，在3 次谐波上线性插值算法拥有最高的幅值精度，但是在其他次谐波幅值的计算上，其精度明显不及另外两种算法。抛物线插值算法在3 次谐波的计算上误差较大，但是在其他谐波幅值的计算上有较高的精度。Hermite 插值算法在低次谐波幅值的计算上和抛物线插值算法精度大致相近，但是在高次谐波的计算中拥有较抛物线插值算法更高的精度，其9 次谐波幅值的相对误差仅为0.12%，明显优于另外两种算法。

不妨进一步加大频率的波动范围以模拟微电网在特殊环境下的非稳态周期信号来测试分段插值算法的性能，在信号不变的前提下，设:

f=50 ×［1 +0.04sin(2π×5t)］

基波频率的变化范围在48 Hz ～52 Hz 之间，变化的周期为0.2 s。在采样频率为6 400 Hz，256 个采样点的前提下对信号进行取样后，用Hermite 插值算法对其进行同步化并FFT 后结果如表3所示。

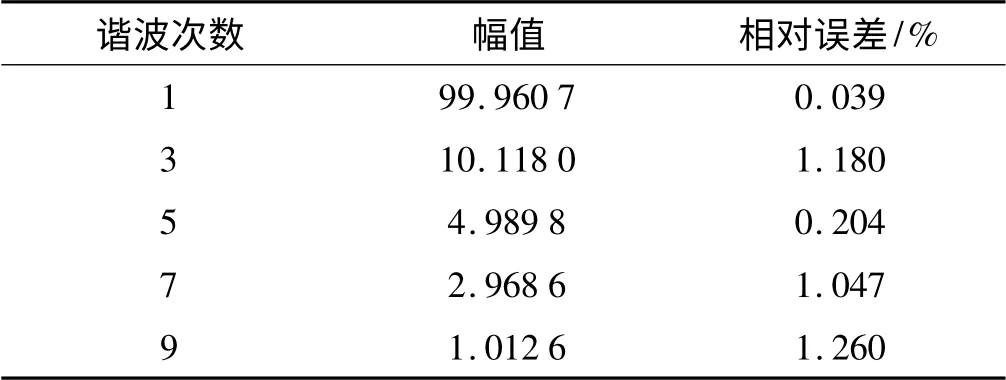
表3 变频信号的仿真结果(2)

由表3 结果可见，即使是频率在48 Hz ～52 Hz 的较大范围波动的非稳态周期信号，在经过Hermite 插值算法的二次同步化之后，其谐波测量的结果也具有相当的精度，其中相对误差最大的是9 次谐波，为1.26%，满足GBT 17626.7—2008 国标要求，在对精度要求不是太高的场合具有一定的应用价值。

5 结束语

本研究提出了一种基于Hermite 插值的时域插值算法用来对非同步采样序列进行同步化处理，并对固定频率偏移和变频率偏移两种情况下的非同步序列进行了仿真和对比。因为本研究对信号采用了截断误差高达四阶的两点Hermite 插值公式进行计算，充分保证了计算精度。同时因为在理论上只需一个完整周期的采样序列就能进行插值同步化计算，该算法也具备了很高的实时性，可以适用于非稳态周期信号等特殊信号的同步化计算。

仿真结果证明，在基波频率偏移范围很大或者基频偏移连续变化的特殊情况下，该算法依然能保持良好的计算精度，能够满足GBT 17626.7—2008 国标要求，是一种有实用价值的非同步取样序列的同步化算法。

［1］苗唯时，张建华，郑云霞.分布式发电对配电系统的影响［J］.陕西电力，2010(1):33-36.

［2］OCHOA L F，PADIHA F A，HARRISON G P.Evaluating distributed generation impacts with a multi-objective index［J］.IEEE Transactions on Power Delivery，2006，21(3):1452-1458.

［3］陈隆道，钱照明，张圣训.周期域分析中非同步取样数据的同步化［J］.电子学报，2001，29(7):1-4

［4］祁才君，陈隆道，王小海.应用插值FFT 算法精确估计电网谐波参数［J］.浙江大学学报:工学版，2003，37(1):112-116.

［5］赵文春，马伟明，胡 安.电机测试谐波分析的高精度FFT 算法［J］.中国电机工程学报，2001，21(12):83-87.

［6］AIELLO M，CATALIOTTI A，COSENTINO V，et al.Synchronization techniques for power quality instruments［J］.IEEE Trans.Instrum.Meas，2007，56(6):1511-1519.

［7］蔡忠法，陈隆道，周 箭.非同步采样的同步化谐波分析算法［J］.浙江大学学报:工学版，2008，42(4):682-685.

［8］王 彭，周 峰，黄震宇.基于时域准同步的谐波和间谐波检测算法［J］.仪器仪表学报，2013，34(2):275-280.

［9］GALLO D，LANGELLA R，TESTA A.On the processing of harmonics and interharmonics:Using Hanning window in standard framework［J］.IEEE Trans.Power Del.，2009，19(1):28-34.

［10］WEN H，TENG Z S，WAHG Y，et al.Simple interpolated FFT algorithm based on minimize sidelobe windows for power-harmonic analysis［J］.IEEE Trans.Power Electron.，2011，26(9):2570-2579.

［11］ZEMG B，TENG Z.Parameter estimation of power system signals based on cosine self-convolution window with desirable side-lobe behaviors［J］.IEEE Trans.Power Del.，2011，26(1):250-257.

［12］CHANG G W，CHEN CI，LIU Y J，et al.Measuring power system harmonics and interharmonics by an improved fast Fourier transformbased algorithm［J］.IET Gener.，Transmiss.Distrib.，2008，2(2):193-201.

［13］周 峰，赵春宇，黄震宇，等.基于时域线性插值的信号周期计算方法及误差分析［J］.仪器仪表学报，2011，32(8):1724-1730.

［14］陈隆道，王小海.周期域分析中的信号周期算法［J］.仪器仪表学报，2001，22(4):410-412.

［15］刘 洋，姜守达，孙圣和.插值法信号周期测量的精度分析［J］.电子测量与仪器学报，2007，21(1):6-10.