计及电动汽车的配电网概率潮流计算及接纳能力分析研究

罗 庆，黄民翔

(浙江大学 电气工程学院，浙江 杭州 310027)

0 引言

随着社会经济的持续发展，能源供应问题将逐渐凸显，环境污染问题也日趋严重。在此背景下，世界各国都在倡导节约能源，降低对化石燃料的依赖性，减少社会经济发展对环境带来的破坏。电动汽车以其能效高、污染小、噪音低的优势被各国政府及汽车企业认为是未来汽车发展的重要方向，是实现节能减排的重要手段之一。

我国从“八五规划”开始在电动汽车领域的研究取得了诸多重要成果。同时我国政府在“十二五”规划中制定了《电动汽车科技发展专项规划草案》，进一步的规划了我国电动汽车的发展方向。

电动汽车作为一种新型的非线性电力负荷，具有随机性、间歇性，如果大规模的接入电力系统，势必会增加某些时段电力系统的负荷。同时也有可能造成电压越线、谐波污染、网损增大等问题［1］。从而对电力系统的稳定安全运行造成一定的负面影响［2-3］。

配电网具有闭环设计、开环运行的特点，是电网向用户供配电的重要环节。考虑到配电网规模庞大、结构复杂，电动汽车负荷的接入将会对配电网造成很大的影响，配电网将从辐射式网络变为含有分布式电源与用户互联的网络。因此研究配电网接入电动汽车是具有重要意义的，而对其影响进行量化分析的主要方法就是进行潮流计算。

实际配电网规模庞大，节点和支路众多，传统的确定性潮流计算很难反映出配电网实际运行情况。而概率潮流计算能很好地反映出配电网中各种随机因素变化对系统的影响，也能考虑电动汽车无序充电引起的配电网负荷的随机变化，同时计算出配电网支路潮流以及节点电压、电流的概率统计特性［4］。

目前，已有许多学者对电动汽车接入电力系统进行了研究分析。文献［5］分析了电动汽车充电对电网的影响，但文中缺少数据支撑;文献［6］针对电动汽车接入配电网的充放电优化问题，建立了以节点电压偏移最小、有功损耗最小、V2G 入网服务成本及车主充电成本最低为目标的NSGA-II 算法，能够很好地处理电网和车主双方的利益;文献［7］建立了插入式电动汽车的电力系统概率潮流模型，并利用三点估计法对处于不同时间段的电力系统进行概率潮流计算，得到潮流结果的统计特性;文献［8］根据美国佛蒙特州常规负荷曲线及电动汽车预测渗透率，分析了电动汽车基于四种控制策略下的充电负荷模型。

本研究在针对电动汽车接入配电网的特点，建立电动汽车功率需求模型。利用Matlab 软件对电动汽车负荷随机接入的IEEE33 节点配电系统进行概率潮流计算，并从电压越限的角度对配电网接入电动汽车的接纳能力进行分析。

1 电动汽车充电功率需求模型

1.1 假设条件

电动汽车充电功率的需求受诸多因素制约，本研究结合目前电动汽车的实际使用情况及其他学者的研究结果，作出如下假设:

(1)电动汽车用户每天只对车辆进行一次充电;

(2)电动汽车每次充电均能充至满电量;

(3)在最后一次出行返回后对电动汽车进行充电;

(4)电池容量为24 kW·h(以启辰晨风为例)。

1.2 电动汽车用户行驶特性

电动汽车的类型、用户充电时间、日行使里程、充电模式等有关因素均会影响电动汽车的充电负荷特性。根据文献［9，10］中美国交通部对全美家用车辆行驶情况的调查结果(national household travel survey，NHTS)，可以得到全美电动汽车用户的统计数据。统计数据先进行归一化处理，再用极大似然估计的方法将电动汽车日行驶里程及最后一次出行返回时刻分别近似为对数正态分布和正态分布［11］。

电动汽车日行驶里程满足对数正态分布，拟合结果如图1 所示。概率密度函数为:

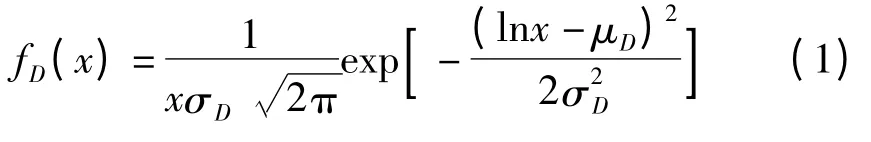
式中:μD=3.20，σD=0.88。

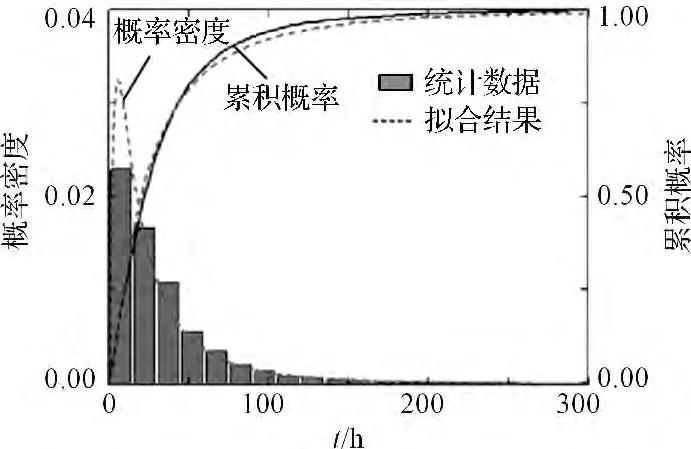
图1 电动汽车日行驶里程

由假设条件可知，电动汽车用户最后一次出行返回时立即对车辆进行充电，其拟合结果如图2 所示。其概率密度函数为:

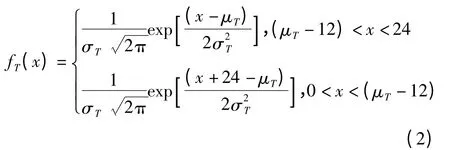
式中:μT=17.6，σT=3.4。

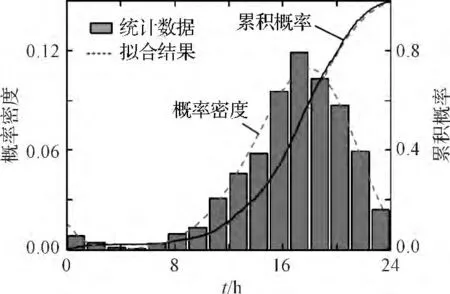
图2 最后一次出行并返回时刻

1.3 电动汽车充电功率需求分析

本研究根据文献［12］建立充电功率需求模型。假设电动汽车充电模式为慢冲模式，充电电压为220 V，充电电流为16 A～20 A，则充电功率在3.5 kW～4.5 kW范围内服从均匀分布，概率密度函数为:

车辆每次充电持续时间Tc的概率密度函数为:

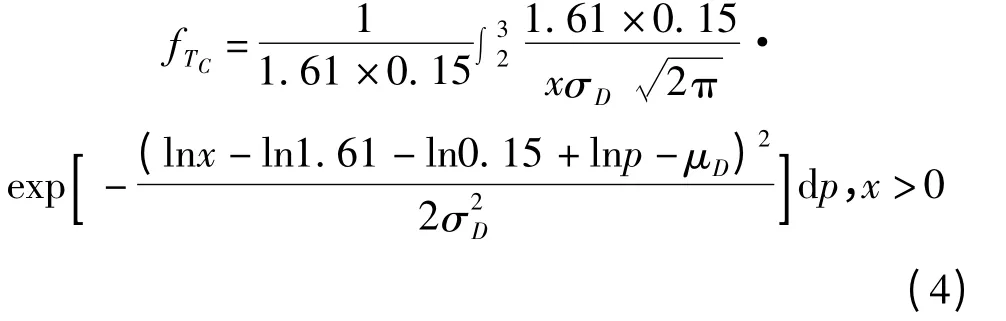
为了描述t0时刻电动汽车的充电状态，本研究引入随机变量，当=1 表示电动汽车正在充电;=0 表示未开始充电或已经充好电。其概率分布为:

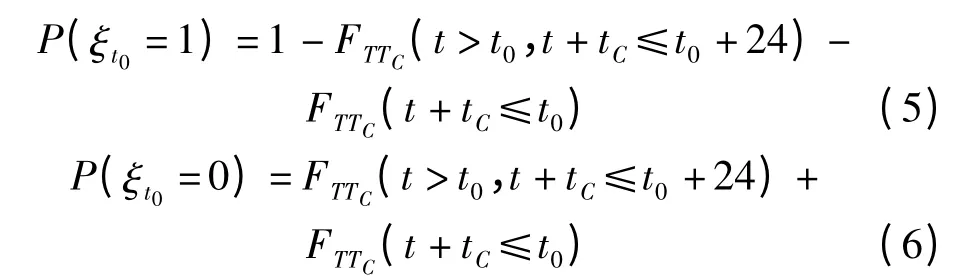
式中:FT，FTC—充电开始时刻、充电时长的概率分布函数。由假设可知两者相互独立。

电动汽车在t0时刻的充电功率需求为:

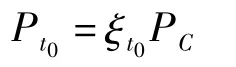
其概率分布为:

本研究通过蒙特卡洛模拟法求出一天内24个整点时刻1 台电动汽车充电功率需求的期望和标准差［13］。利用Matlab 软件求出的结果如图3 所示。

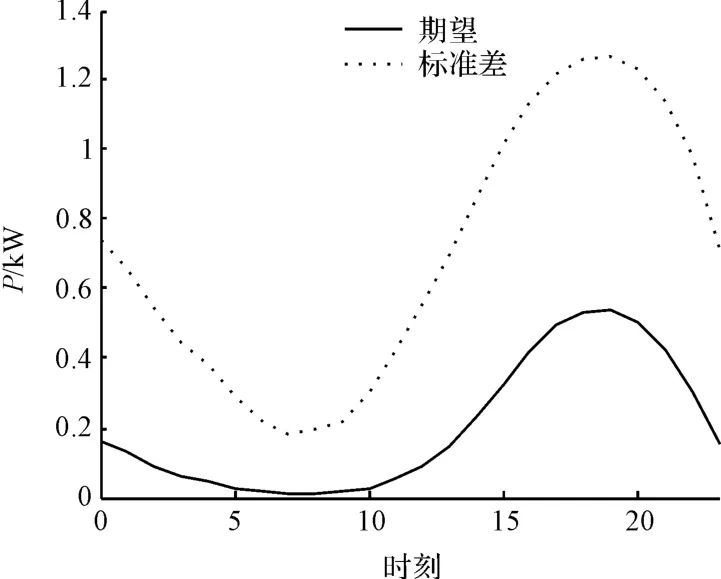
图3 1 台电动汽车充电功率需求的期望及标准差

若一天中有N 台电动汽车需要充电，在t0时刻电动汽车总功率需求为所有电动汽车在此时刻的充电功率之和，总充电功率可为:

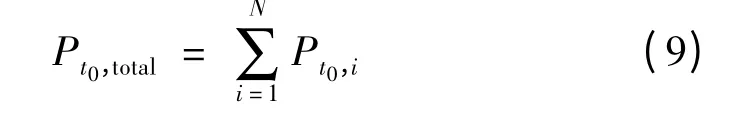
利用Matlab 计算结果如图4 所示，此时取N=10 000台。

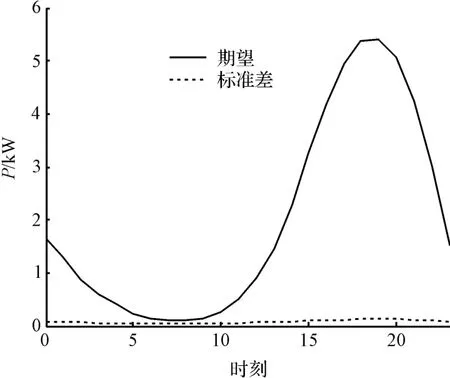
图4 10 000 台电动汽车充电功率的期望和标准差

2 潮流计算与接纳能力分析

2.1 概率潮流计算

在实际配电网中，由于电力系统负荷变化及预测均具有不确定性，如线路故障、设备故障或负荷波动等，电网中的潮流分布情况在本质上是不确定的。本研究用概率论与数理统计的理论来描述这种随机性，建立相应的数学模型，从而对电网进行潮流计算，这种方法称为概率潮流研究［14］。

概率潮流计算可用于分析节点电压、支路电流、线路潮流的期望值、方差及概率分布等数学统计特性，可以更深刻地反映电网的运行状况，为规划与运行决策提供更可靠的信息。

2.2 计及电动汽车充电负荷的概率潮流计算

概率潮流计算的实质是求解带有随机变量的潮流方程，考虑电动汽车负荷随机接入配电网，此时输入随机变量为部分节点的注入功率，输出随机变量为节点电压幅值、相角及支路潮流。在进行潮流计算时，本研究采用基于回路电流的前推回代法给出配电系统各节点电压、电流、支路功率的期望、方差、概率密度函数等数学统计特性。

(1)基于支路电流的前推回代法

对于具有n个节点的辐射型配电网络，假定其根节点电压为U0、各节点负荷为Pi+Qi(i=1，2，…，n－1)，相邻i、j 两节点之间的阻抗为Rij+jXij，网络拓扑结构给定，待求量为各节点电压、各节点注入电流、支路潮流及网络损耗。各节点的注入电流可由下式表示:

由式(10)结合网络拓扑结构计算各支路中的电流，某支路的电流Ii为该支路末节点及所有位于该支路下游节点的注入电流之和，表达式如下:

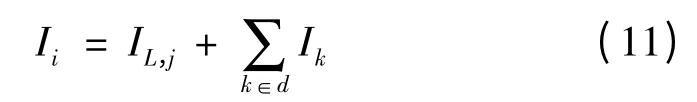
本研究得出整个配网系统所有支路电流后，从根节点起，利用已知支路阻抗和支路电流就按各支路的电压降，并更新各节点电压。对于始端编号i、末端编号j 的支路，其末端电压可由下式求出:

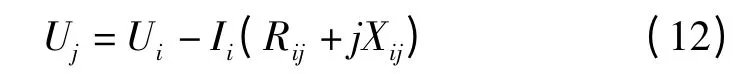
重复前推支路电流过程和回代节点电压过程，最终得出配电网潮流计算结果。

(2)基于前推回代法的配电系统潮流计算流程图如图5 所示。

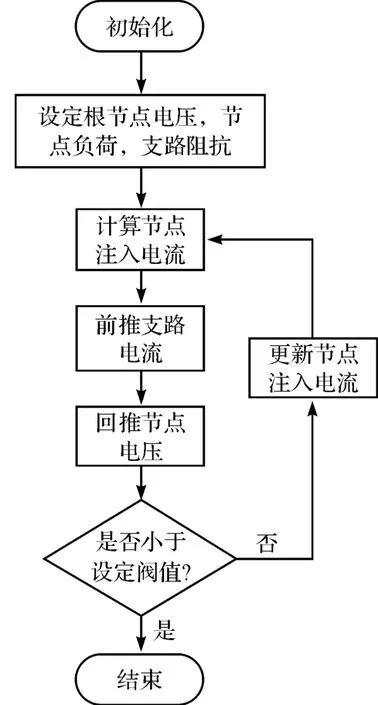
图5 配电系统潮流计算流程图

2.3 电动汽车接纳能力的概念与评价标准

电动汽车作为电力系统的一种新型负荷，在充电时间及空间上具有随机性，其接入电网充电将会影响电力系统的正常运行。若单辆或少量电动汽车接入电网充电，其对于庞大的电力系统来说相当于一个微小扰动，对电网的影响较小甚至可以忽略不计;但大规模电动汽车接入电网充电将会严重影响电力系统的安全稳定运行。因此，配电系统在同一时刻能接入的电动汽车数量是有限的。

笔者通过第1 节建立的电动汽车充电功率需求模型，将电动汽车随机接入配电系统，利用概率潮流计算可得节点电压、支路电流、线路潮流的期望值、方差及概率分布等数据，不妨以接纳能力来衡量配电系统能接入的电动汽车数量的最大值。电动汽车接纳能力可定义为在满足电力系统安全、可靠、稳定运行的条件下，允许接入电动汽车数量的最大值。

电网的接纳能力可通过多方面来评价，如电压越限、导线载流量、支路功率及网络损耗等，本研究重点介绍电压越限。

电力系统中某一节点的实际电压Ui与额定电压Ue之差占额定电压Ue的百分比称为该节点的电压偏差ΔU%，即:

供配电系统运行方式和节点负荷的变化会导致配电系统各节点的电压也随之发生变化，电压偏差过大会造成电压越限，危害电力系统的安全、可靠、稳定运行。

由《电能质量一供电电压允许偏差》可知，10 kV及以下电压允许偏差为额定电压的。本研究以10 kV的中压配电网系统为例进行计算分析，配电系统中任一节点电压超过额定电压的即认为发生电压越限，配电系统将不能保证电能质量和系统的安全稳定运行。

3 案例分析

3.1 概率潮流计算

本研究基于Matlab 软件编制了计及电动汽车充电负荷的概率潮流计算程序，采用IEEE33 节点配电系统，接线图如图6 所示。IEEE33 节点配电系统有32条支路，1个电源，网络电压基准值为12.66 kV，三相功率基准值为10 MVA，网络总负荷为3 715 kW +j2 300 kVar。

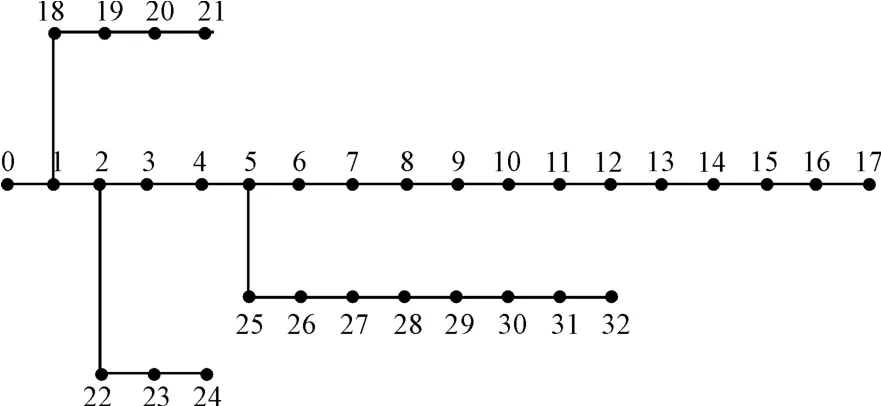
图6 IEEE33 节点配电系统接线图

IEEE33 节点配电系统根节点电压由主变压器分接头确定，本研究假设分接头选为+2.5%，即根节点电压标幺值为1.025。每次仿真时利用软件产生1～32 之间的随机数作为电动汽车接入节点，本研究考虑10 000 台电动汽车随机接入上述配电系统。

结合第1 节建立的电动汽车充电功率需求模型，笔者通过蒙特卡洛采样法(采样500 次)，利用Matlab软件求出一天24 h 中33个节点的电压期望、方差如表1 所示。

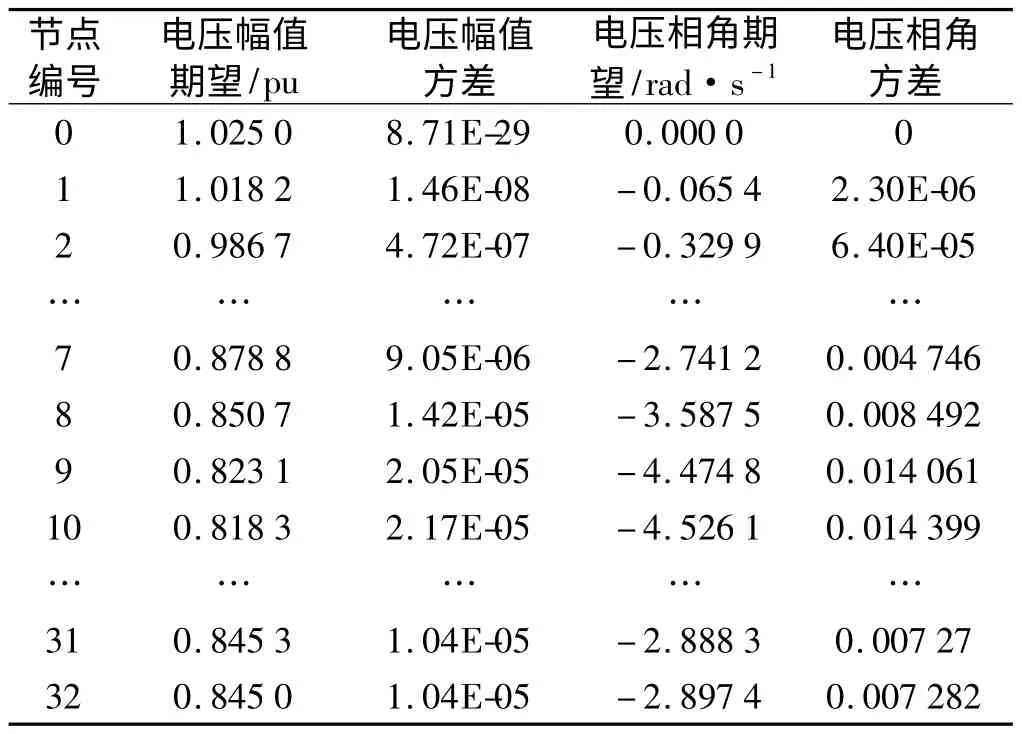
表1 节点电压的期望、方差

注入节点电流的期望、方差如表2 所示。

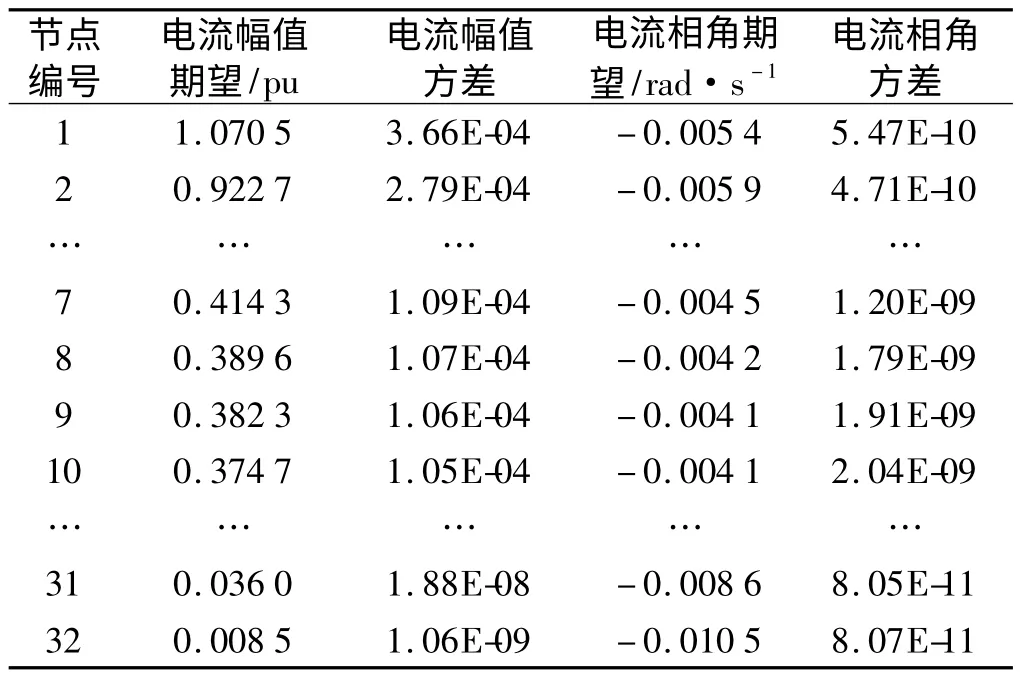
表2 节点电流的期望、方差

支路始端潮流的期望、方差如表3 所示。

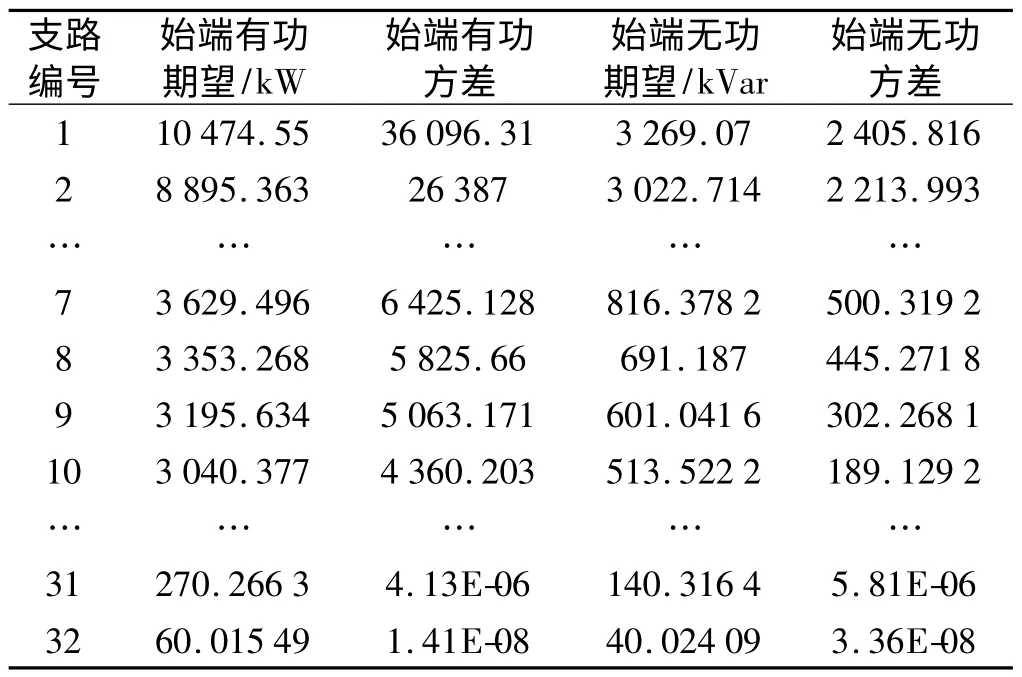
表3 支路始端潮流的期望、方差

笔者以第9 节点为例，画出了第9 节点的节点电压、注入第9 节点的电流及第8－9 支路始端潮流的概率密度函数的图形，分别如图7、图8、图9、图10 所示。

3.2 接纳能力计算

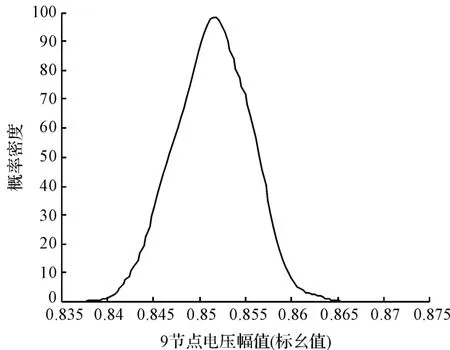
图7 第9 节点的节点电压幅值概率密度函数

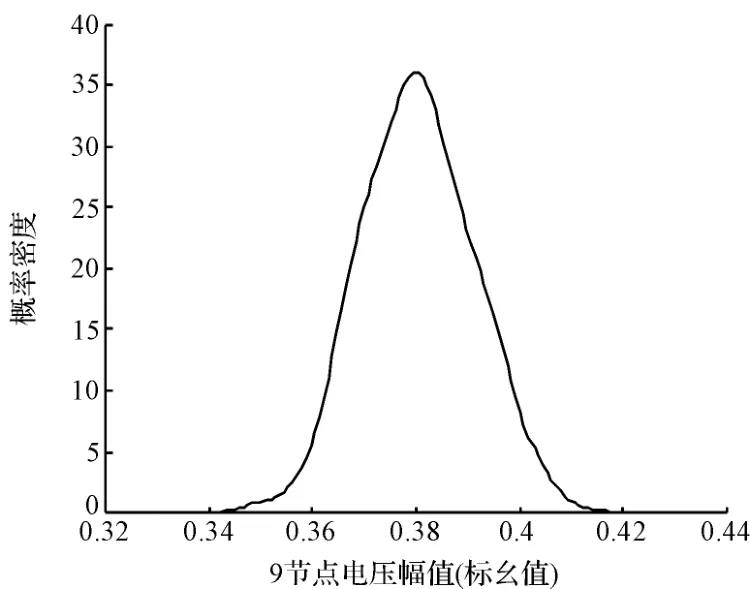
图8 第9 节点的电流幅值概率密度函数

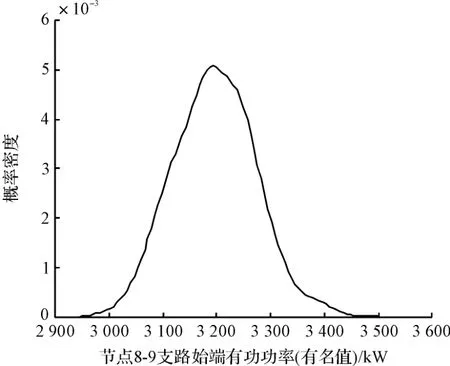
图9 第8－9 支路始端有功功率的概率密度函数

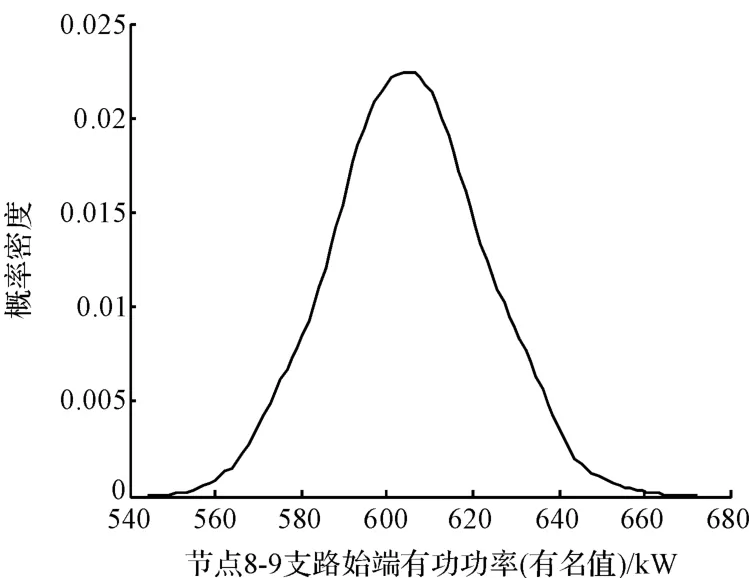
图10 第8－9 支路始端无功功率的概率密度函数

根据接纳能力的定义，某一特定系统应该保证在任何时刻允许接入的电动汽车数量不超过其最大限值，由图4 可知，电动汽车充电功率需求最大值出现在下午19:00 左右，因此本研究根据19:00 时刻允许接入的最大电动汽车数量来确定整个配电系统的接纳能力。

由于允许的电压偏差范围为，系统中只要有一个节点的电压高于1.07 或低于0.93，即视为不能保证系统的安全稳定运行。因此，当电压偏差最大的节点的电压为1.07 或0.93，此时接入的电动汽车数量即为电网对电动汽车的接纳能力。

本研究利用Matlab 软件算出在接入充电的电动汽车数量不同的情况下，电压偏差最大节点的电压Ux大小如表4 所示。

表4 接入不同电动汽车数量对应的节点电压偏差

由表4 可知，当配电系统中随机接入的电动汽车数量为2 400 辆时，系统中电压偏差最大节点的电压值为0.929 8，因此可近似认为系统的接纳能力为2 400 台。

4 结束语

电动汽车作为电力系统一种新型负荷，其并入电力系统必然会对电网的正常运行造成一定影响。本研究以2001年NHTS 的调查数据为基础，采用蒙特卡洛模拟法求出了单台及多台电动汽车功率需求的期望与标准差。

针对IEEE33 节点配电系统，考虑电动汽车负荷的随机接入，本研究进行了概率潮流计算，计算出系统各节点电压、注入电流、支路功率的期望、方差、概率密度函数等数学统计特性。

本研究介绍了电动汽车接纳能力的概念与评价标准，并从电压越限的角度分析了配电网接入电动汽车的接纳能力。

计算结果表明，随着接入电动汽车数量的增加，系统节点电压也会随之降低，为了保证电力系统稳定安全的运行，当电动汽车数量增加到一定程度时，系统中部分节点将产生电压越限问题，导致电能质量降低，危害电力系统安全运行，因此必须将接入充电的电动汽车控制在一定数量内。

［1］李 梁，袁 军，高一凡，等.计及电动汽车充电站的配电网综合优化研究［J］.机电工程，2014，31(11):75-80.

［2］王 旭，齐向东.电动汽车智能充电桩的设计与研究［J］.机电工程，2014，31(3):394-397.

［3］MEYERS M K，SCHNEIDER K.Impacts assessment of plug-in hybrid vehicles on electric utilities and regional U.S.power grids part 1:technical analysis［R］.Richland，Washington，USA:Pacific Northwest National Laboratory，2007.

［4］徐国钧，刘永胜.基于层次分析和概率模拟的电动汽车对配网负荷影响研究［J］.电力系统保护与控制，2012，40(22):38-45.

［5］高赐威，张 亮.电动汽车充电对电网影响的综述［J］.电网技术，2011，35(2):127-131.

［6］李恵玲，白晓民.电动汽车入网技术在配电网的应用研究［J］.中国电机工程学报，2012，32(增刊):22-27.

［7］吴晨曦，文福拴.含有风电与光伏发电以及电动汽车的电力系统概率潮流［J］.电力自动化设备，2013，33(10):8-15.

［8］STEVEN L.Plug-in hybrid electric vehicles and the Vermont grid:a scoping analysis［R］.Vermont:University of Vermont Transportation Center，2007

［9］TAYLOR M J，Alexander A.Evaluation of the impact of plug-in electric vehicle loading on distribution system operations［C］//IEEE Power ＆ Energy Society General Meeting，Calgary，Canada，2009:1-6.

［10］VYAS A，SANTINI D.Use of national surveys for estimating‘full’PHEV potential for oil use reduction［EB/OL］.2008-07-21.

［11］蔡德福，钱 斌.含电动汽车充电负荷和风电的电力系统动态概率特性分析［J］.电网技术，2013，37(3):590-596.

［12］田立亭，史双龙，贾 卓.电动汽车充电功率需求的统计学建模方法［J］.电网技术，2010，34(11):126-130.

［13］罗卓伟，胡泽春，宋永华，等.电动汽车充电负荷计算方法［J］.电力系统自动化，2011，35(14):36-42.

［14］丁 明，李生虎，黄 凯.基于蒙特卡罗模拟的概率潮流计算［J］.电网技术，2001，11(11):10-15.