一道赛题的四种解法
2015-01-19 08:44曹群林
新课程(中学) 2015年10期
曹群林
(江西省信丰中学)
(2013 年全国高中数学联赛江西省预赛第6 题)
解法1 三角换元
所以x-2∈[0,1],3-x∈[0,1].
又因为(x-2)+(3-x)=1,
故f(x)的值域是[1,2].
解法2 代数换元
,目标函数为z=u+v 的线性规划问题.
故f(x)的值域是[1,2].
解法3 求导
故f(x)的值域是[1,2].
解法4 构造概率分布列
因为Dξ=Eξ2-(Eξ)2≥0,
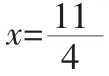
故f(x)的值域是[1,2].
猜你喜欢
中等数学(2022年7期)2022-10-24
中等数学(2022年5期)2022-08-29
中等数学(2022年1期)2022-06-05
中等数学(2022年2期)2022-06-05
中学生数理化·七年级数学人教版(2021年12期)2021-12-31
艺术大观(2020年11期)2020-10-09
——信丰阁
城乡建设(2019年14期)2019-02-20
现代园艺(2018年1期)2018-03-15
中学教学参考·理科版(2017年8期)2018-02-24
中学生数理化·高三版(2017年2期)2017-04-21

