基于混沌理论的河流藻类生长特性分析——以德国易北河为例

赵晓东, 张宏建, 周洪亮

1 工业控制技术国家重点实验室, 浙江大学, 杭州 310007 2 中国计量学院计量测试工程学院, 杭州 310018

基于混沌理论的河流藻类生长特性分析
——以德国易北河为例

赵晓东1,2,*, 张宏建1, 周洪亮1

1 工业控制技术国家重点实验室, 浙江大学, 杭州 310007 2 中国计量学院计量测试工程学院, 杭州 310018

针对藻类生长具有高度非线性特征和实际采样样本间隔稀疏的问题，采用了混沌理论对采样序列的混沌特征量进行估计。采用C-C方法估计时间序列的嵌入维和延迟时间，采用G-P算法对关联维进行估计，并采用小数据量法估计最大Lyapunov指数，最终可实现对最长可预测时长的估计。以易北河为例，对易北河水体叶绿素a 1997年至2001年间各年的观测序列进行了混沌分析，分析结果表明，各年的叶绿素a观测序列均具有低维混沌特性，关联维D=2.75—4.02，各年的叶绿素a序列的最长预测时间变化范围为8.01—18.94 d，平均为13.98d(约2周)。采用同样方法对5a易北河连续日径流量时间序列分析表明，该径流量也具有低维混沌特性(最大Lyapunov指数λ1=0.0125)，径流量的最长预测时间估计约为80 d。气候因素的混沌特性对藻类生长表现出的混沌特征的影响可能要大于径流量等水文因素的影响。

藻类生长; 混沌; 关联维数; Lyapunov指数

水体藻种浓度指标实际上是多藻种浓度指标的综合体现，受限于藻种种群间生长与竞争特性。Huisman等[1]给出了多藻种在不同营养条件下的数值模拟，藻种生长显示出具有混沌特性，藻种显示出平衡条件下的多样性。文中只针对恒定营养盐输入进行了数值模拟，并未给出试验验证结果。自1978年，Connell等[2]提出非平衡营养条件下的 “中等干扰假说”后，对水生环境非平衡营养输入条件下引发的藻种多样性进行了大量的数值模拟和实验研究[2- 8]。国内研究者在对两种常见水华藻类进行 “脉冲”营养盐输入条件下的实验室培养的研究过程中，发现具有相同初始生长条件的藻种在非稳态营养输入条件下显示出截然不同的竞争特性，在生物量上表现出交替占优的特征[9]。对于实际河流藻类生长观测序列而言，河流下游某观测点获得的藻类生长数据与上游藻类生长具有相关性。影响其相关性的因素除沿途期间的气象因素之外，河流径流量也是主要影响因素之一[10]。可见，河流中藻类这种生长不确定特征除营养盐输入因素影响之外，还包括水文和气象条件等因素的影响。在影响藻类生长的各种因子中，早在1987年，Tsonis和Elsner就证明了气候系统是混沌系统[11]，对于河流径流量以及降雨量等水文数据的研究也表明具有混沌特征[12- 15]。

在对地表水体中藻类生长机理进行描述时，水体网格的划分细密程度，各“藕联”数据的测量精度都会对最终藻类预测产生影响，而当该系统具有混沌特性时，上述计算或测量误差都会对藻类长期预测结果产生极大影响，最终导致不可预测。另外，由于藻类指标实际采样样本间隔稀疏(理论上应无穷小)以及藻类生长本身具有高度非线性特征，有必要对藻类实测时间序列是否具有混沌特性进行分析。目前，尽管各种预测方法都针对特定湖库和河流能给出了较为成功的应用，但对于究竟能最大预测多长时间国内外并未有文献给出这方面的报道。因此，对于河流藻类预测而言，有必要对其观测序列是否混沌进行研究，实现对其可预测时长的估计。

本文对混沌理论和所采用的经典的混沌分析算法进行了说明，并以易北河为例，对叶绿素a观测序列和日径流量的时间序列进行了混沌特征量估计，以此判断是否该时间序列具有混沌特征。并在此基础上，对该时间序列的最大可预测时间进行了估计，并指出了可能成为影响藻类生长混沌特性的主要外部因素。

1 分析方法

1.1 Takens定理和相空间重构理论

Takens[16]证明了可以找到一个合适的嵌入维，在这个嵌入维空间里可以把有规律的轨迹恢复出来。该定理表明，可以将单变量时间序列重构成一个相空间，只要嵌入维数足够高，就可构建出一个拓扑等价的相空间。由于混沌系统的策动因素是相互影响的，因而在时间上先后产生的数据点也是相关的，Packard等[17]提出了采用原系统中某变量的延迟坐标来重构相空间。因此重构相空间时，只对一个分量在固定时延点上进行维向量拓展至三维甚至更高维的空间，就可以重构一个拓扑等价的相空间。

设x(t)，t=1,2,…,N为观测时间序列。重构相空间选择嵌入维数m，时间延迟设为τ，则由x(t)构造出一组新的向量序列X(ti)={x(ti),x(ti+τ),…,x(ti+(m-1)τ)}T，i=1,2,…,M，M=N-(m-1)τ，如式(1)所示:

(1)

即

X(t)={X(t1),X(t2),…,X(ti),…,X(tM)}

式(1)表明，时间延迟τ和嵌入维数m的选择是相空间重构的主要内容，直接影响到相空间重构质量和其奇异吸引子特征量的描述。

1.2 时间延迟的选取

对于无限长、无噪声的时间序列，时间延迟τ的选择原则无限制，但对于有限时间序列，相空间的特征量则依赖于τ。Taken[16]认为时间延迟和嵌入维数两者理论上相互独立无关，两者可以单独确定。也有研究者认为两者的选择应互相关联[18-19]，延迟时间的选取应依赖于延迟时间窗口，即τw=(m-1)τ。

本文主要采用C-C方法进行时间延迟估计，并采用互信息算法计算结果作为对比。互信息量方法是估计重构相空间时间延迟的一种有效方法。该方法利用互信息函数的第一次极小值来确定相空间重构的时间延迟，Fraser等给出了互信息计算的递归算法[20]。Kim等人[19]提出了C-C方法，即通过嵌入时间序列的关联积分构造统计量来代表非线性时间序列的相关性，对时间延迟τ和时间窗口τw同时进行估计。该方法效果和互信息量法一致，但能有效减少互信息法的计算量，并能保持其非线性特征，且对小数据组可靠，抗干扰能力较强。

1.3 嵌入维数的确定

相空间嵌入维数需要足够大，以便能刻画出该系统的奇异吸引子。奇异吸引子是描述混沌系统时间序列的重要特征，其维数一般低于相空间的维数。关联维数D常用于描述奇异吸引子的维数，嵌入维数的选取通常要求m≥2D+1。本文采用饱和关联维法(G-P算法) 求取关联维数。

Grassberger和Proacaccia[21]依据是嵌入定理和相空间重构理论提出的求取关联维的G-P算法，只需针对实验观测数据就可以得到吸引子维数，目前采用较多：

对于嵌入维数为m的一组向量序列维{Xi}i=1,2,…,N，其中Xi={xi1,xi2,…,xim}为参考点，分别计算其它N-1个点与Xi的距离，统计落在以Xi点为中心且距离小于正数r的点的个数。向量之间的距离一般采用两种方法，2-范数和∞-范数。两种方法的计算距离的公式是拓扑等价的，后者计算量较小[22]。式(2)所示采用的是∞-范数计算，即以两个向量的最大分量差作为距离:

(2)

满足该条件的矢量对数在种配对中所占比例被称为关联积分:

(3)

其中表示Heaviside阶跃函数:

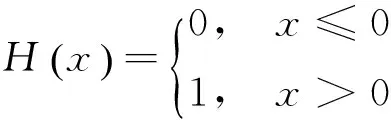
(4)

令dm为m维空间中的奇异吸引子最大伸展距离，r≥dm时Cm(r)=N(N-1)/N2=(N-1)/N,当N→∞时，Cm(r)≈1。实际上，Cm(r)反映了奇异吸引子中各点之间距离的分布概率，则有:

(5)

根据分形理论的标度不变性，当r位于无标度区间时，D(m,r)是与m和r有关的常数，称为关联指数，是关联维数D的确定逼近。取小距离r1和r2，则有：

(6)

对式6两边取对数，则有:

(7)

当值∣r2-r1∣很小时，可认为D(m,r2) ≈D(m,r1)。则有:

(8)

由式(8)可知，D(m,r)是lnCm(r)—lnr曲线的斜率。当r→0时，可获得关联维数D的近似值:

(9)

确定关联维的关键是先确定无标度区间。实际动力系统的分形不同于数学上的分形所具有的在无穷尺度上的自相似或自仿射性，而是近似地或统计意义上存在自相似，这种自相似仅存在于一定的尺度变化范围，一旦超出了这个尺度变化范围，其自相似性就不复存在，这个尺度变化范围就是分形的无标度区。根据标度区间不变性定理，无标度区间内，Cm(r)与r成指数关系，如式(9)。标量的取值应包含在分形的无标度区之内，其序列长度不应少于20，以保证估计到的关联维可靠且满足相关性检验[23]。近些年，针对无标度区间的确定方法已展开多方面的研究[24- 27]。这些确定的方法有效性和针对性虽然不相同，但其基本步骤均是：1) 改变嵌入维m值，获得lnCm(r)-lnr的曲线簇；2) 用最小二乘法拟合每条曲线最佳直线段(无标度区)，获得该直线段的斜率作为嵌入维数m对应的关联指数；3) 随着m的增加，关联指数会出现饱和现象，此时最佳直线段对应的斜率即为该混沌序列对应的关联维数D。

1.4 最大Lyapunov指数的估计方法

混沌系统可通过其吸引子的宏观特征量表征。宏观特征量主要包括：关联维，Kolmogorov熵，Lyapunov指数等。其中，Lyapunov指数的时间数列是根据序列本身所计算出来的客观规律，是量化初始闭轨道的指数发散和估计方法的混沌量，反映了动力系统整体混沌量水平。因此，Lyapunov指数计算对预测混沌时间序列而言显得尤为重要。

在判断实际动力系统是否为混沌系统时，通常只估计最大Lyapunov指数λ1。小数据量法是只计算最大Lyapunov指数的一种方法，是通过对基本轨道上每个点的最近邻近点的平均发散速率估计出最大Lyapunov指数。该算法需要给定嵌入维数，时间延迟以及序列的平均周期。考虑到小数据量算法对嵌入维数，时间延迟，数据序列长度以及信噪比的敏感程度较低，具有较好的鲁棒性[28]，本文采用了该算法实现对最大Lyapunov指数的求取。但为避免计算过程中参数选取的主观性，采用了C-C方法对嵌入维数和时间延迟同时估计。其平均周期的计算是将序列FFT变换获得的每个功率值先与其对应的周期加权，再最终求加权平均计算获得[29-30]。本文只对时间序列的最大Lyapunov指数进行求取，该指数是否大于零可用来判别一个时间序列是否为混沌系统。

1.5 Lyapunov时间计算

最大Lyapunov指数λ1表示的是当前两相邻轨道距离最大分量的指数发散程度：

(10)

式中，δx(0)表示两相邻轨道初始距离, δx(t)表示经过时间后的轨道距离。混沌运动并不是真正的随机，他服从确定性的规律，这表明在一定的临界距离变化范围内是可以预测的，而超过这个范围时，轨道运动就不可预测了[27, 31]。距离变化如式(11)所示，达到临界值所经历的时间如式(12)所示:

(11)

(12)

通常认为轨迹分离达到原间距的数倍或十几倍时，轨道就不确定了。此时可认为lnC≈1，则:

(13)

式(13)所示的时间为Lyapunov时间，也称为最大预测时间。当λ1越大，预测时间越短，系统运动的可预测性越差。

2 分析结果

本文主要对易北河1997年—2001年的叶绿素a观测序列进行了混沌特性分析。易北河全长1094km，为欧洲第四大内陆河，流域面积达148268 km2。流域面积主要覆盖捷克和德国，叶绿素a的测点位置为Geesthacht Weir(N53°25.486′ E10°20.665′)，并采用在线叶绿素监测仪(10-AU-005)每小时采样1次。本文采用C-C算法[19]进行时间延迟τ的确定，采用G-P算法[21]对数据序列的关联维数进行估计D，进而确定嵌入维数m，并采用Rosenstein方法[27]计算了叶绿素a观测序列的最大Lyapunov指数λ1，对最大预测时间t0进行了估计。

2.1 时间延迟估计

每年的叶绿素a观测数据序列通过C-C方法获得的时间延迟(图1)。时间延迟τ=tτs，τs为采样时间间隔，取值为1，则τ=t。曲线第一个极小值所对应的t为时间延迟，图中所示时间延迟为8或12，该迟延与互信息法所确定的时间基本一致(图1)。互信息法中时间延迟对应曲线第一个极小值。

时间延迟τ比较如表1所示。采用互信息方法和C-C方法获得τ差异较小，表明这两种方法在τ的判断上比较接近。本文选用C-C方法获得的τ值进行关联维数的计算。

2.2 关联维数估计

针对1997—2001年的叶绿素a观测序列采取了C-C方法获得时间延迟τ (表1)，并采用G-P算法获取了对应各年份的关联维数D，如图2所示，其中标度r起始值分别参考空间向量距离的最小值和最大值，其步长设定为30。无标度区间的确定方法是采用目前常用的视觉识别方法。

图2所示，每年的叶绿素a的观测序列均具有低维分形维。通过C-C算法获得的最佳嵌入维数与通过G-P算法中获得的饱和嵌入维数相接近，如表2所示。饱和嵌入维数是指最佳直线段斜率刚达到饱和时所对应的嵌入维数。当增加超过饱和嵌入维数时，其直线段斜率变化趋于稳定，由G-P算法可知，对应的最佳直线段斜率值即为关联维数。

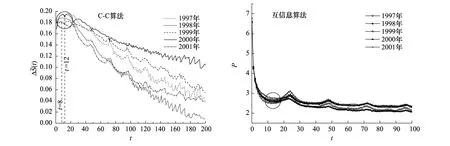
图1 叶绿素a观测序列时间延迟τ (τ=t)Fig.1 The time delay of the sequence of hourly chlorophyll a observation (τ=t)

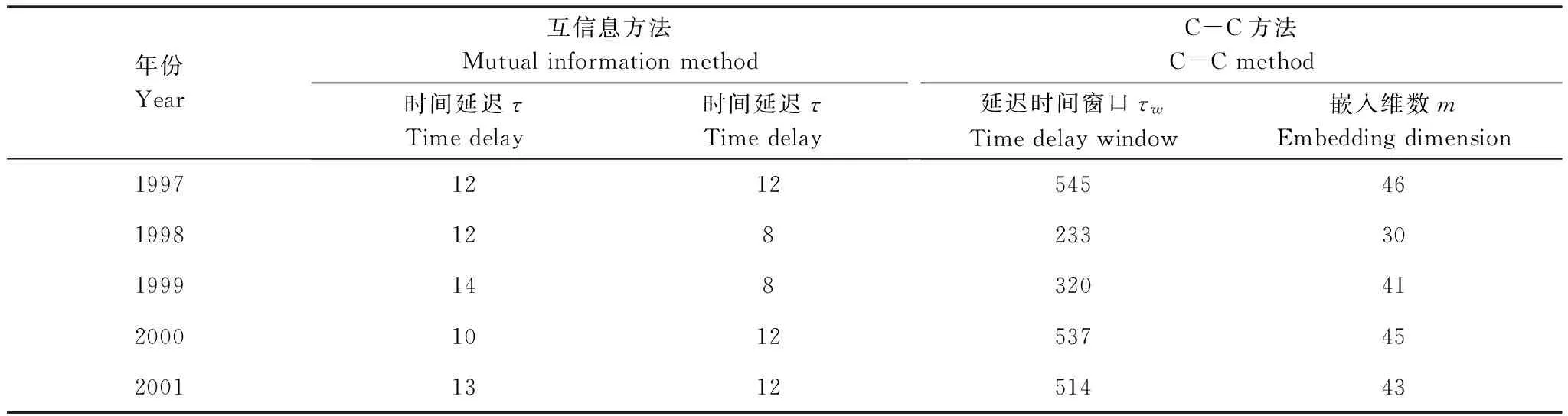
表1 叶绿素a观测序列时间延迟不同算法计算结果比较*

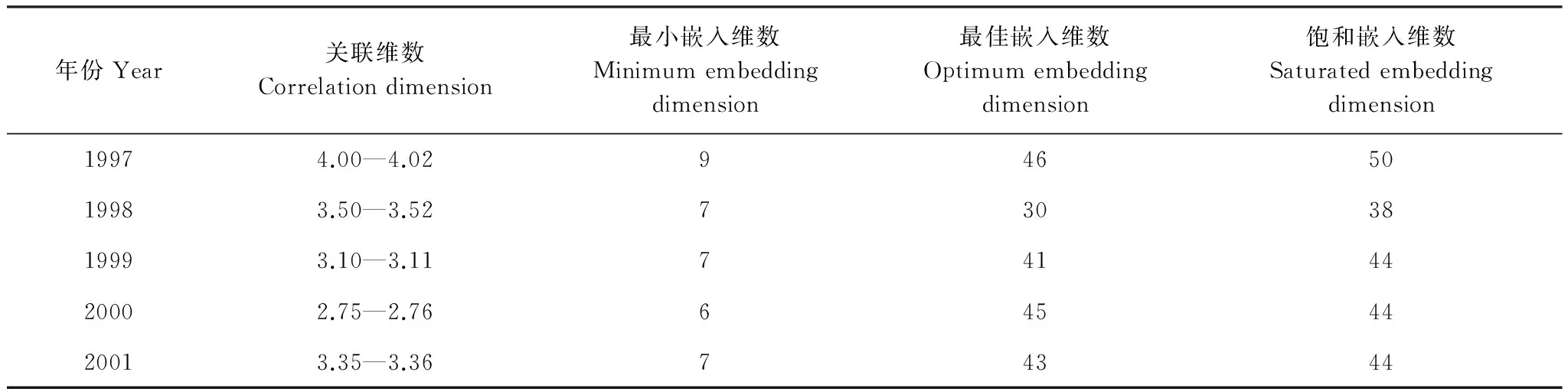
表2 各年关联维数和嵌入维数列表

2.3 最大Lyapunov指数估计

选取C-C方法计算所得的嵌入维数m和时间延迟τ，如表1，根据Rosenstein算法[28]，结果如图3所示。图中横坐标表示为离散时间步长，纵坐标ln表征近邻点对在第i个离散时间步长后的距离对数值。图3所示，在i=20—100的范围内，曲线表现出较好的直线特性。选取该区域，采用最小二乘法做出回归直线，该直线的斜率即为最大Lyapunov指数λ1。Rosenstein算法中根据时间序列的平均周期限制相空间中最近邻点的短暂分离，时间序列平均周期的算法参考Rathje等[29-30]提出的算法。每年叶绿素a浓度时间序列的平均周期如图3中tp值所示。

如表3所示，各年的叶绿素a观测序列的最大Lyapunov指数均为非零数，表明其时间序列具有混沌特性，Lyapunov指数接近于零值，表明该时间序列混沌特性较弱。5a的叶绿素a观测序列最大预测时间最大约为19 d，最短约为8 d，平均约为14 d (两周)。

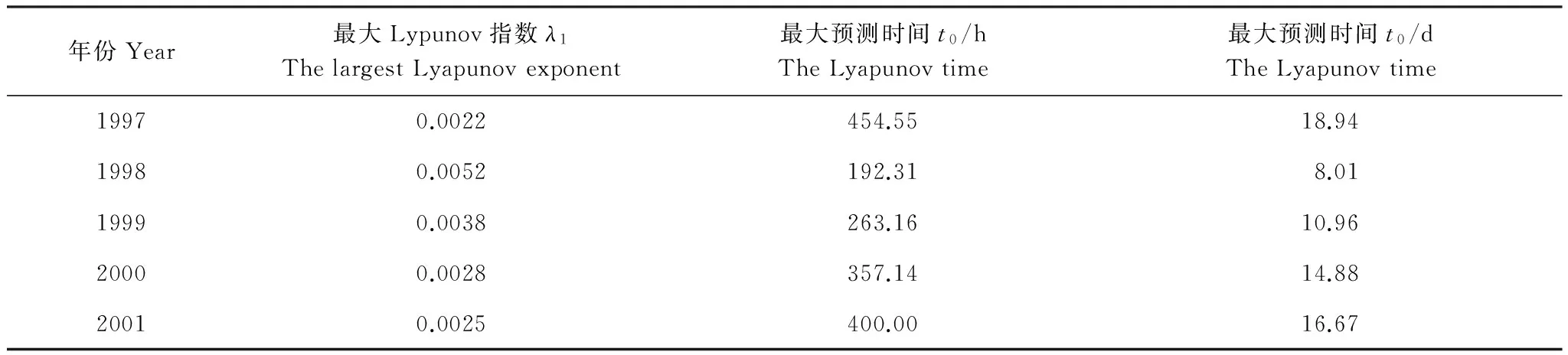
表3 不同年份最大Lyapunov指数和最大预测时间列表

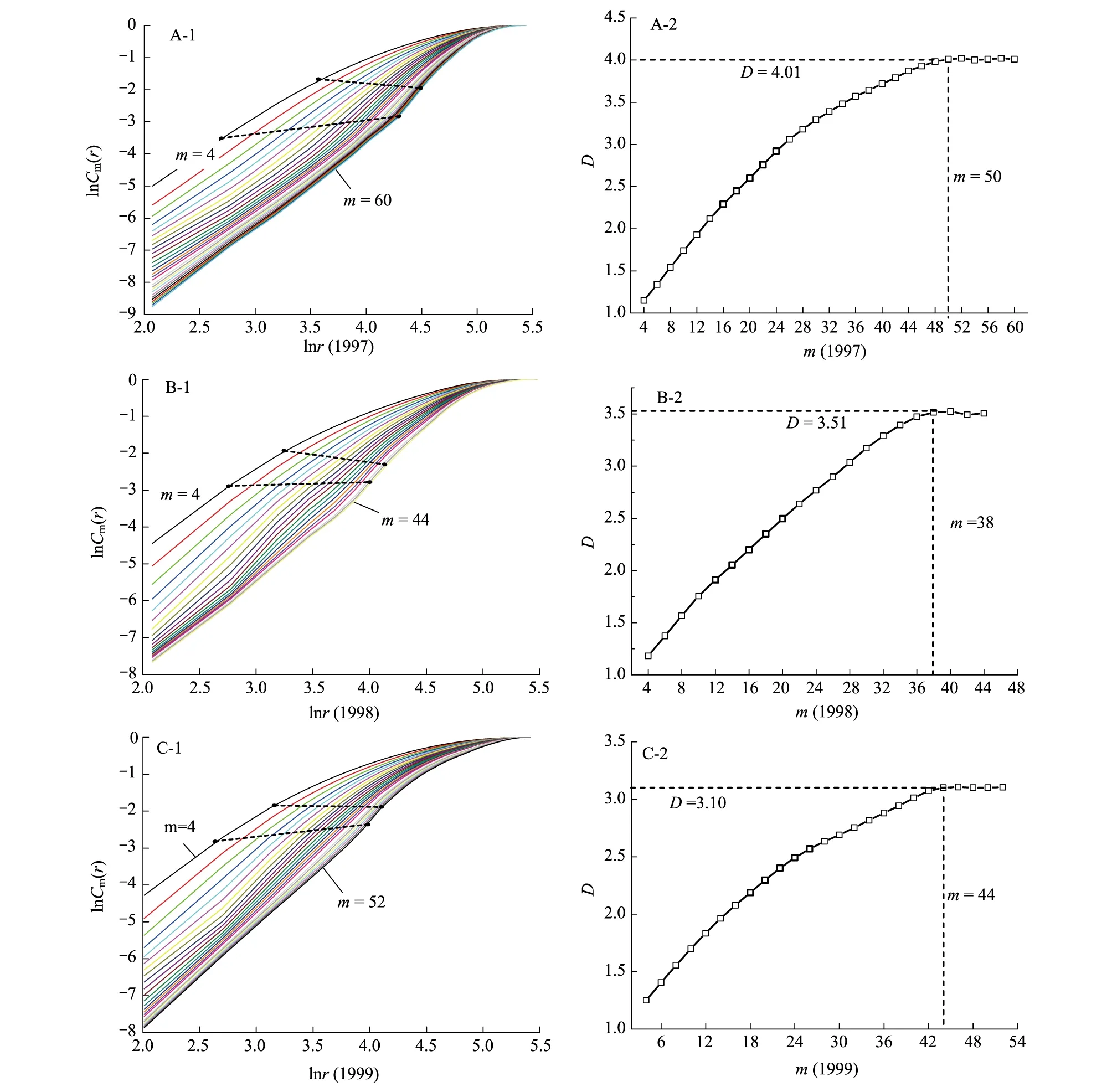
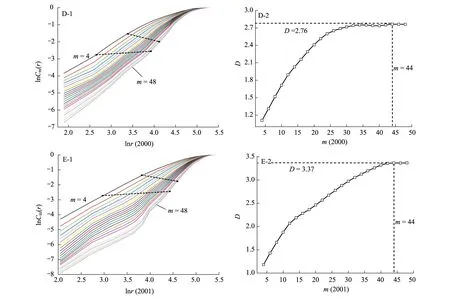
图2 叶绿素a观测序列关联维数Fig.2 The correlation dimension D of hourly chlorophyll a observation sequence

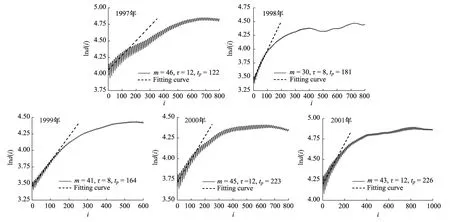
图3 不同年份叶绿素a观测序列Lyapunov指数(Rosenstein算法)Fig.3 The largest Lyapunov index of the chlorophyll a sequence estimated by the small-data method

2.4 河流日流量时间序列混沌特性分析

采用与叶绿素a观测序列同样的分析方法，对易北河1997年3月3日至2001年10月31日之间的日径流量时间序列进行混沌特性分析，流量采样点位置为Neu Darcha((N53°14.207′ E10°53.314′)，采样设备为多普勒测流仪，每日采样一次。首先采用了C-C方法同时对延迟时间窗口和时间延迟同时估计。C-C方法中的最小值对应时间延迟窗口值，的第一个零点或者的第一个极小值对应着时间延迟(τ=t)。由图4可知，tw=60，τ=17，其中的第一个零点对应值为τ=60。通常取较小值作为时间延迟，避免使得非线性模型的拟合关系复杂，降低难度和减少计算量[24]。C-C方法后的时间延迟与互信息法计算结果相接近，后者τ=15，对应曲线的第一个极小值。

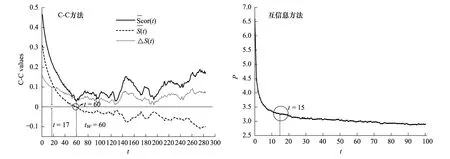
图4 1997—2001年易北河日径流量时间序列时间延迟Fig.4 The time delay of the daily runoff sequence (1997—2001)

1997—2001年易北河日径流量时间序列饱和关联维数为9，如图5所示。而C-C方法获得的tw和τ，根据可得tw=(m-1)τ，m=5。G-P算法获得的关联维数D=1.84，则日径流量时间序列的嵌入维数m≥2D+1。同样，C-C算法获得的嵌入维数也满足此条件。

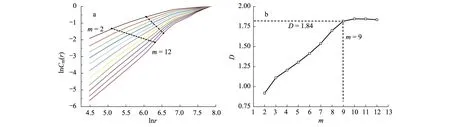
图5 1997—2001年易北河日径流量时间序列关联维数Fig.5 The correlation dimension of the daily runoff sequence (1997—2001)

根据Rosenstein算法，取m=5，τ=17，tp=26(平均周期)，计算结果如图6，由图中观察可知，在0—100的范围内具有直线上升趋势，采用最小二乘法对该范围进行直线拟合，获得直线段斜率，即估计最大Lyapunov指数为λ1=0.0125，估计最大预测时间为80d。非零数的指数估计和关联维数表明日径流量同样具有混沌特性。

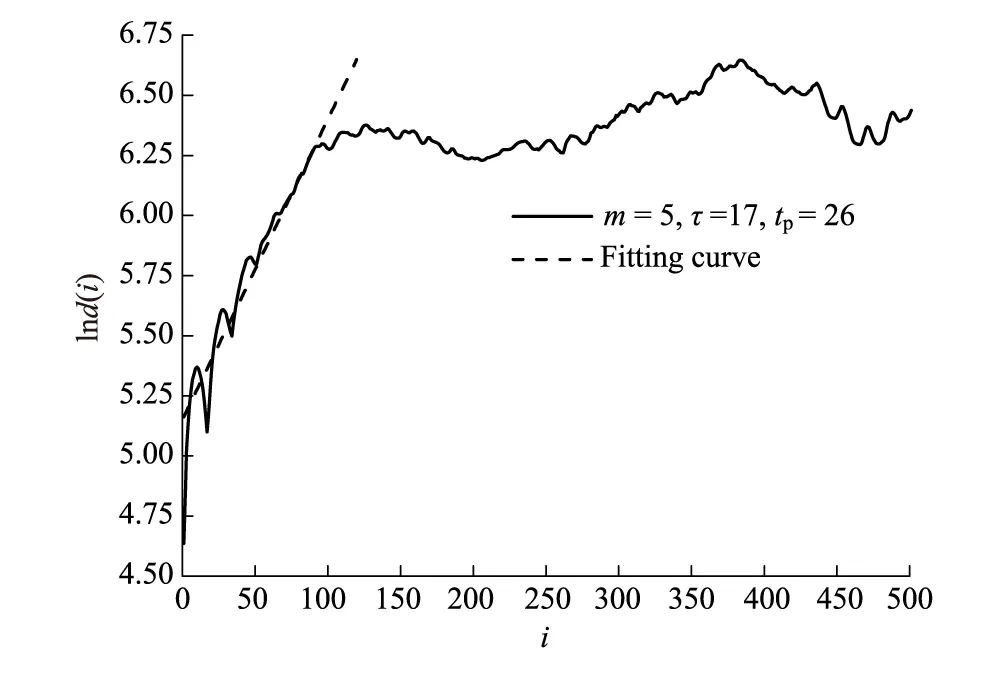
图6 1997—2001年易北河日径流量时间序列Lyapunov指数(Rosenstein算法)Fig.6 The largest Lyapunov index of daily runoff sequence (1997—2001)

3 结果讨论

采用两种方法即C-C方法和互信息法进行了时间序列时间延迟的判定，从叶绿素a观测序列和日径流量时间序列的分析结果可知，两种方法各自获得的时间延迟比较接近，如表1，图4所示。在重构相空间时，τ不取最佳值只会影响关联维数的计算，并不会影响重构吸引子如实反映系统的动力学性质[27]。τ取值太小，迫使空间轨迹沿同一方向挤压，信息被压缩，获取困难。反之，导致相邻时刻的动力学状态变化剧烈，使得简单的系统运动变得看起来很复杂。采用C-C方法获得的τ依赖于时间延迟窗口τw，τw反映了数据依赖的最大时间，而互信息方法仅仅反映了第一次局部最大时间，不能估计τw。另外，评价重构吸引子的质量是其几何上的重复性和不相关性，重构吸引子应具有较低的重复性和较强的相关性。因此，τw是一种用于估计维数的更好的量。尽管C-C方法是利用统计结果获得，但通过和互信息对比表明，在确定序列时间延迟上仍具有较好的效果，而且该方法能同时确定嵌入窗口和嵌入维数，为较好的估计Lyapunov指数提供了前提条件。

为更好的验证C-C方法计算嵌入维数的可靠性，采用了G-P算法对嵌入维数进行估计。计算结果表明，通过G-P算法获得的饱和嵌入维数与C-C方法获得嵌入维数相近，如图2和图5所示。这进一步验证了C-C方法的可靠性。

根据G-P算法获得关联维数过程中，对无标度区的估计采用了视觉识别法。无标度区的判断尽管有很多种方法[25-26, 32]，但在无法获知理论关联维数的情况下，视觉识别法仍可作为一种方便快捷的估计方法。如图2所示，当m取较小值时，其直线段(无标度区)较为明显，直线区间范围较大。随着m的增加，其直线段范围发生变化，并有逐渐变小的趋势，如图2中的曲线包围范围所示，这与文献[23]描述结果一致。该方法获得关联维数的精度对判定系统混沌特性以及确定关联维数并无显著影响[33]，而且由C-C方法确定的嵌入维数均比获得由关联维数确定的最小嵌入维数大得多(>2D+1)，确保展开的相空间与原系统的动力学特性拓扑等价。同样，叶绿素a序列的低关联维数估计值表明藻类生长在较低维空间产生自相似，但藻类生长的复杂性可能使得需要采取高的嵌入维数值才能完全展现藻类的生长轨迹特征。

采用Rosenstein算法对最大Lyapunov指数进行了估计，先后对叶绿素a和日径流量时间序列进行了指数估计。结果表明，两种时间序列的最大Lyapunov指数估计值均较小，如表2，图6所示，这表明该序列的邻近吸引子轨道离散程度较低，可以进行较长时期的预测。其中，5a的日净流量的最大预测时间估计为80d，5a的叶绿素a最大预测时间平均为14d，前者要远大于后者。可见，尽管河流径流量对叶绿素a有影响，但可能并不是对后者产生混沌特性影响的主要因素。

河流水体中的藻中生长的另一个重要因素是天气条件，而气候系统已被证实是具有混沌特性。目前天气预报可以被较好预测的时间约为15d，和叶绿素a观测序列的最大预测时间相吻合。相比于水文条件，气候条件可能是对叶绿素a的混沌特性产生影响的一个主要因素。

在Elbe河流中的硅藻几乎总是优势藻种，其限制性营养盐为硅。因此，叶绿素a所反映的主要是硅藻浓度，始终作为优势藻，使得由于藻种间的竞争导致的混沌现象似乎不可能发生，另外，其限制性营养盐硅输入主要是来自于Elbe河源头的Elbe砂岩山的硅砂岩土层，而沿途补充的营养源多为氮磷，因此，由于营养盐输入变化导致的藻种浓度出现混沌特征可以忽略。这也说明了气象因素要相对于其他因素更有可能造成藻种叶绿素a浓度的混沌变化。

4 总结

采用了混沌理论对易北河叶绿素a1997年至2001年间各年的观测序列进行了混沌分析，分析结果表明，各年的叶绿素a观测序列均具有低维混沌特性，同样在对5a易北河连续日径流量时间序列分析表明，该径流量也具有低维混沌特性。通过对两种序列的最大可预测时间比对表明径流量等水文因子可能并不是影响叶绿素a混沌特性的主要因素，相反气象因子可能占据主导地位。

致谢：Mr.Scharfe博士提供德国易北河历史数据,特此致谢。

[1] Huisman J, Weissing F J. Biodiversity of plankton by species oscillations and chaos. Nature, 1999, 402(6760): 407- 410.

[2] Connell J H. Diversity in tropical rain forests and coral reefs. Science, 1978, 199(4335): 1302- 1310.

[3] Sala S, Vighi M. GIS-based procedure for site-specific risk assessment of pesticides for aquatic ecosystems. Ecotoxicology and Environmental Safety, 2008, 69(1): 1- 12.

[4] Malmaeus J M, Blenckner T, Markensten H, Persson I. Lake phosphorus dynamics and climate warming: a mechanistic model approach. Ecological Modelling, 2006, 190(1/2): 1- 14.

[5] Hu W P, Jørgensen S E, Zhang F B. A vertical-compressed three-dimensional ecological model in Lake Taihu, China. Ecological Modelling, 2006, 190(3/4): 367- 398.

[6] 饶群, 芮孝芳. 完全混合系统总磷随机模型研究. 水科学进展, 2002, 13(1): 21- 25.

[7] Xu F L, Jørgensen S E, Tao S, Li B G. Modeling the effects of ecological engineering on ecosystem health of a shallow eutrophic Chinese lake (Lake Chao). Ecological Modelling, 1999, 117(2/3): 239- 260.

[8] Hassan H, Hanaki K, Matsuo T. A modeling approach to simulate impact of climate change in lake water quality: phytoplankton growth rate assessment. Water Science and Technology, 1998, 37(2): 177- 185.

[9] 赵晓东, 潘江, 李金页, 陶晓磊, 庞坤. 铜绿微囊藻和斜生栅藻非稳态营养盐限制条件下的生长竞争特性. 生态学报, 2011, 31(13): 3710- 3719.

[10] Scharfe M, Callies U, Blöcker G, Petersen W, Schroeder F. A simple Lagrangian model to simulate temporal variability of algae in the Elbe River. Ecological Modelling, 2009, 220(18): 2173- 2186.

[11] Tsonis A A, Elsner J B. The weather attractor over very short timescales. Nature, 1988, 333(6173): 545- 547.

[12] Radhakrishnan P, Dinesh S. An alternative approach to characterize time series data: case study on Malaysian rainfall data. Chaos, Solitons and Fractals, 2006, 27(2): 511- 518.

[13] 丁晶, 王文圣, 赵永龙. 长江日流量混沌变化特性研究——Ⅱ相空间嵌入维数的确定. 水科学进展, 2003, 14(4): 412- 416.

[14] 丁晶, 王文圣, 赵永龙. 长江日流量混沌变化特性研究——Ⅰ相空间嵌入滞时的确定. 水科学进展, 2003, 14(4): 407- 411.

[15] Sivakumar B. Rainfall dynamics at different temporal scales: a chaotic perspective. Hydrology and Earth System Sciences, 2001, 5(4): 645- 652.

[16] Takens F. Detecting strange attractors in turbulence. Lecture Notes in Mathematics, 1981, 898: 366- 381.

[17] Packard N H, Crutchfield J P, Farmer J D, Shaw R S. Geometry from a time series. Physical Review Letters, 1980, 45(9): 712- 716.

[18] Kugiumtzis D. State space reconstruction parameters in the analysis of chaotic time series-the role of the time window length. Physica D: Nonlinear Phenomena, 1996, 95(1): 13- 28.

[19] Kim H S, Eykholt R, Salas J D. Nonlinear dynamics, delay times, and embedding windows. Physica D: Nonlinear Phenomena, 1999, 127(1/2): 48- 60.

[20] Fraser A M, Swinney H L. Independent coordinates for strange attractors from mutual information. Physical Review A, 1986, 33(2): 1134- 1140.

[21] Grassberger P, Procaccia I. Characterization of strange attractors. Physical Review Letters, 1983, 50(5): 346- 349.

[22] 王安良, 杨春信. 评价奇怪吸引子分形特征的Grassberger-Procaccia算法. 物理学报, 2002, 51(12): 2719- 2729.

[23] 党建武, 黄建国. 基于G. P算法的关联维计算中参数取值的研究. 计算机应用研究, 2004, 21(1): 48- 51.

[24] 韩敏. 混沌时间序列预测理论与方法. 北京: 中国水利水电出版社, 2007.

[25] 党建武, 施怡, 黄建国. 分形研究中无标度区的计算机识别. 计算机工程与应用, 2003, 39(12): 25- 27.

[26] 巫兆聪. 分形分析中的无标度区确定问题. 测绘学报, 2002, 31(3): 240- 244.

[27] 吕金虎, 陆君安, 陈士华. 混沌时间序列分析及其应用. 武汉: 武汉大学出版社, 2002.

[28] Rosenstein M T, Collins J J, De Luca C J. A practical method for calculating largest Lyapunov exponents from small data sets. Physica D: Nonlinear Phenomena, 1993, 65(1/2): 117- 134.

[29] Rathje E M, Abrahamson N A, Bray J D. Simplified frequency content estimates of earthquake ground motions. Journal of Geotechnical and Geoenvironmental Engineering, 1998, 124(2): 150- 159.

[30] Rathje E M, Faraj F, Russell S, Bray J D. Empirical relationships for frequency content parameters of earthquake ground motions. Earthquake Spectra, 2004, 20(1): 119- 144.

[31] 刘式达, 梁福明, 刘式适, 辛国君. 自然科学中的混沌和分形. 北京: 北京大学出版社, 2003.

[32] 陈敏. 一种简单的GP算法无标度区识别方法. 计算机与信息技术, 2007, (11): 35- 36, 39- 39.

[33] 姬翠翠, 朱华, 江炜. 混沌时间序列关联维数计算中无标度区间识别的新方法. 科学通报, 2010, 55(31): 3069- 3076.

[34] Smith L A. Intrinsic limits on dimension calculations. Physics Letters A, 1988, 133(6): 283- 288.

[35] 洪时明, 洪时中. 用Grassberger-Procaccia方法计算吸引子维数的基本限制. 物理学报, 1994, 43(8): 1228- 1233.

[36] 林振山. 长期预报的相空间理论和模式. 北京: 气象出版社, 1993.

Analysis of the growth characteristics of river algae based on chaos theory: a case study of Elbe River

ZHAO Xiaodong1,2,*, ZHANG Hongjian1, ZHOU Hongliang1

1StateKeyLaboratoryofIndustrialControlTechnology,ZhejiangUniversity,Hangzhou310007,China2CollegeofMetrologicalandMeasurementEngineering,ChinaJiliangUniversity,Hangzhou310018,China

Algal growth at equilibrium is not sustainable in a river or lake experiencing point or non-point source pollution, which is likely to change with season, location, and human activity. Chlorophyll a, as a common indictor, is an important reference point for water resource management. It can be affected by the biodiversity of species, as a result of their oscillations, and chaotic fluctuations. Algal growth has many highly nonlinear characteristics. The characteristics that differ among species, however, are all susceptible to change under external disturbance. It is difficult to provide a comprehensive and detailed description of nonlinear algal growth. Variations in chlorophyll a tend to maintain certain regularity; for example, seasonal variation and the 24 hour cycle, which also display self-similarity. However, it is difficult to observe similar variations at different times from the studied sampling series. These features are similar to aspects of chaotic motion, such as boundedness, ergodicity, and inherent randomness. The sampling of the indictor chlorophyll a is typically performed on an hourly, weekly, or even monthly basis. With higher sampling frequency, the sampling series of chlorophyllain the field becomes more unstable and appears to be more chaotic. Therefore, this paper aims to study the variations in a chlorophyll a series sampled from the field, rather than constructing a theoretical model to recapitulate the field data. While there is extensive research on algae in many lakes or rivers, few studies discuss the prediction of algal growth times in aquatic environments. The aspects of algal growth times are partially addressed in this study.The variation characteristics of the algal data series were analyzed using chaos theory. The characters of the one-dimensional time series were recovered by reconstruction into the multi-dimensional phase space, using phase space reconstruction. The reconstruction parameters, namely the embedding dimensionmand time delayτ, were estimated using the correlation integral method (C-C method). The correlation dimension,D, is the basic mathematical description of the strange attractor, which is the main characteristic of a chaotic system.Dwas calculated using the Grassberger-Procaccia algorithm (G-P algorithm). Only the largest Lyapunov exponent,λ1, was estimated through the small data method to evaluate the diffusion degree of the phase trajectory. The reciprocal ofλ1is the upper bound of the deterministic prediction time in the chaotic system, which is designated as the Lyapunov timet0. This property indicates that the system is unpredictable beyondt0. In this paper, the chaotic characteristics of hourly chlorophyll a concentrations and the daily runoff time series of the Elbe River over a five year period (1997—2001) were analyzed. It was found that both sequences had the properties of low-dimension chaos withλ1>0,D= 2.75—4.02 for the chlorophyll a series, andD= 1.84 for the runoff series. The average value oft0(14 days) was estimated for the five-year chlorophyll a sequence data. These findings were remarkably close to the current biggest day-to-day weather forecast time (two to three weeks). A much longer value oft0for the runoff series, for the same period, was 80 days. This result indicated that compared to the weather factors, the runoff factor is clearly weaker in affecting the chaotic characteristics of chlorophyll a.

algal growth; chaos; correlation dimension; Lyapunov exponent

中央高校基本科研业务费专项资金资助(2014FZA5008)

2013- 11- 05;

日期:2014- 11- 03

10.5846/stxb201311052669

*通讯作者Corresponding author.E-mail: zhaoxd@cjlu.edu.cn

赵晓东, 张宏建, 周洪亮.基于混沌理论的河流藻类生长特性分析——以德国易北河为例.生态学报,2015,35(17):5585- 5596.

Zhao X D, Zhang H J, Zhou H L.Analysis of the growth characteristics of river algae based on chaos theory: a case study of Elbe River.Acta Ecologica Sinica,2015,35(17):5585- 5596.