基于ADS的滤波器类型选择对滤波性能的影响分析

朱齐媛，陈新原

（岭南师范学院 信息科学与技术学院，广东 湛江 524048）

射频和微波的广泛应用使射频电路设计领域得到了工业界的特别关注，新兴半导体器件使得高频电路系统不断扩张，这些应用在无线通信、全球定位及雷达等行业中有目共睹。但是，射频设计挑战在通信行业存在更加普遍，46%以上的通信设计工程认为射频设计是最大的技术挑战之一。在通信产品设计中，射频问题比较多地表现在电路匹配、接收灵敏度、器件参数一致性等问题。现代射频和微波系统的设计越来越复杂，对电路的指标要求也越来越高，电路的功能越来越丰富，电路的尺寸越来越小，却要设计周期越来越短，传统的设计方法已经不能满足微波电路设计的需求，使用微波EDA（Electronic Design Automation，电子设计自动化）软件工具进行微波系统的设计已经成为微波电路的设计的必然趋势。ADS—Advanced Design System，是美国安捷伦（Agilent）公司所发开的电子设计自动化软件，功能强大，仿真手段丰富多样，并对设计结果进行成品率分析越优化，大大提高了复杂电路的设计效率，是优秀的微波电路、系统信号链路的设计工具[1-3]。不同于传统的射频分析设计软件，ADS软件不再是简单地用表格的方式计算出射频系统增益和功率预算，而是对射频器件级进行深入的仿真分析。利用ADS软件工程师可以精确分析系统中的噪声、阻抗、互调、隔离、谐波等对系统工程的影响。

射频滤波器是射频电路中最基本也是最常用的射频器件，可以是有微波线构成的，也可以是由电感、电容等集总参数元件构成的[4]。理想的滤波器可以分为4种：低通滤波器、高通滤波器、带通滤波器和带阻滤波器。按照滤波器的制作方法和材料，射频滤波器可以分为波导滤波器、同轴线滤波器、带状线滤波器和微带滤波器。在实际工程应用中，各种滤波器的设计是很复杂的，但是都可以通过将经典的低通滤波器原型，通过不同的变换，将其转换成要求的滤波器。经典的低通滤波器主要有巴特沃斯、切比雪夫和椭圆函数滤波器等[5]，本文用最简单的电路，利用ADS仿真得到不同原型对于滤波性能的影响。

1 滤波器类型选择实例

选择的双端低通滤波器模型（low-pass filter DT），预设滤波器的参数如下，Ap（dB）=0.1，Fp=0.2 GHz，Fs=1.2 GHz，如图 1所示。选择不同的滤波器类型，首先选择的是巴特沃斯滤波器，即在Response Type中选择Maximally Flat，之后得到滤波器的子电路图，如图2所示，选择S参数仿真，得到滤波器的S21、S11、S12参数曲线（滤波器电路相对于输入和输出端口来说是对称的，这种滤波器可以用在天线前端，作为收发公用的滤波器，所以曲线S21、S12参数曲线是相同的）。设置M1、M2点，满足设计要求，即在100 MHz处的通带内损耗为-0.09 dB，滤波器在100 MHz的频点处输入反射系数为-17 dB。

图1 双端低通滤波器模型Fig.1 Double end of the lowpass filter

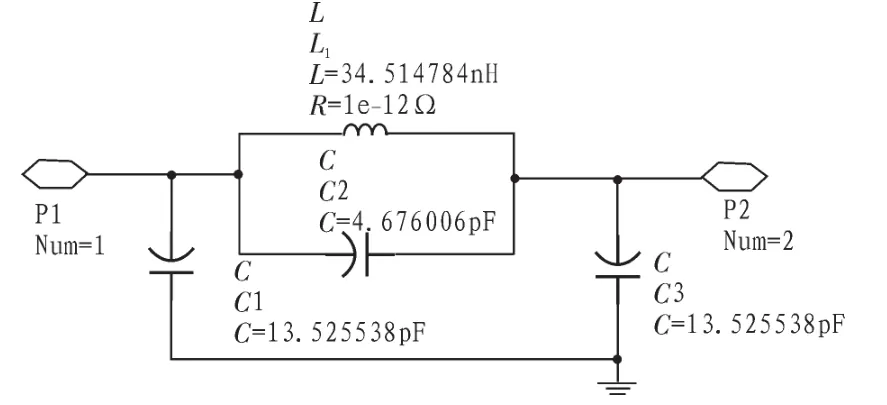
图2 巴特沃斯滤波器子电路Fig.2 Butterworth filter circuit

其次选择切比雪夫滤波器，即在Response Type中选择Chebyshev，之后得到滤波器的子电路图，选择S参数仿真，同样可以得到滤波器的 S21、S11、S12参数曲线。在图中设置 M1、M2点，满足设计要求，即在100 MHz处的通带内损耗为-0.48 dB，滤波器在100 MHz的频点处输入反射系数为-9.86 dB。

最后选择椭圆函数滤波器，即在Response Type中选择Elliptic，之后得到滤波器的子电路图，选择S参数仿真，得到滤波器的 S21、S11、S12。在图中设置 M1、M2点，满足设计要求，即在100 MHz处的通带内损耗为-0.48 dB，滤波器在100 MHz的频点处输入反射系数为-9.83 dB。

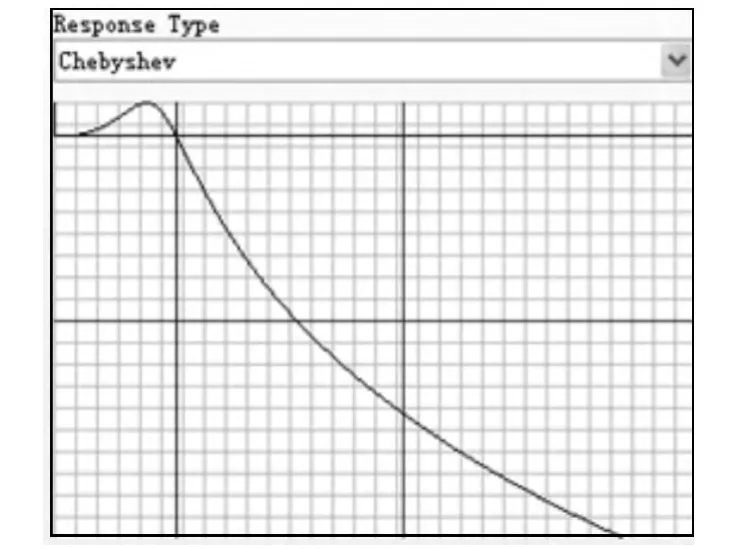
图3 响应类型为切比雪夫Fig.3 Response type for the Chebyshev

图4 切比雪夫滤波器S21、S11参数曲线Fig.4 Chebyshev filter S21、S11 curves

2 不同类型滤波器的滤波性能分析

从上节的数据中可以看出，3种不同响应类型的选择均可以满足滤波器的基本要求，但是各自还是有很多的不同，从类型选择方面可以看出，巴特沃斯滤波器最大的优点是通道内具有较高的平坦度，但是明显的缺陷是通带和阻带间的过渡特性较差，不够陡峭，相对滤波器的理想特性较差；在陡峭方面比较好的是切比雪夫滤波器，但是换来的牺牲是通带内的衰减特性不平坦，呈现波纹特性；过渡特性较好的是椭圆函数构建的滤波器，但是此类滤波器阻带衰减不再趋于无限大，而是呈现波纹特性[6]。在模拟滤波器的设计中，需要找到一个可用电路实现的传输函数，来满足滤波器的频率响应曲线，滤波器的设计最关键的研究工作，就是找这个电路可实现的传输函数找到了一种传输函数，并且提出了实现这种函数的电路结构。但是由于传输函数的曲线只是近似满足理想滤波器的要求，具体选择何种结构，需要综合考虑。切比雪夫滤波器滚降更加陡峭，也就是窗型系数好，但是在通带（阻带）内频率响应有等幅波动，巴特沃斯滚降不够陡峭，但是在通带内是最平坦的。从以上的分析可以清晰的看出，滤波器的截止陡峭度和线性相位特性是相互冲突，在具体的设计中要折中考虑。同样的电路形式，元件参数不同就变成了不同的滤波器，同一种滤波器也可以用不同的电路形式实现。滤波器类型按信号处理特性需求来选择，例如衰减率Chebyshev>Butterworth>Bessel，阶跃响应是 Bessel>Butterworth>Chebyshev，而Butterworth和 Bessel是带内增益无抖动，Chebyshev I是带内增益有抖动，Chebyshev II是带外衰减有抖动等等，怎么选择要和信号紧密结合，需要综合考虑。

3 结束语

在射频滤波器的分析和设计中，不同类型的低通滤波器原型会给之后的结果带来不同的效果，通过对同一低通滤波器的类型选择差异，利用先进的ADS仿真软件，从幅频响应特性和群时延两个角度，展示了巴特沃斯、切比雪夫和椭圆函数3种基本类型滤波器性能分析，实现不同性能指标滤波器设计中类型选择的方向。为工程师对于滤波器的设计提供了很好的方向选择，有一定的学术价值。

[1]陈艳华，李朝晖，夏玮.ADS应用详解——射频电路设计与仿真[M].北京：人们邮电出版社，2009.

[2]冯新宇，车向前，穆秀春.ADS2009射频电路设计与仿真[M].北京：电子工业出版社，2010.

[3]南敬昌，冯永生，刘元安.基于ADS线性射频放大器设计与仿真[J].计算机仿真，2007（5）:302-305.NAN Jing-chang，FENG Yong-sheng，LIU Yuan-an.Design and simulation of linear small-signal transistor’s 1.5 GHz amplifier[J].Computer Simulation，2007（5）:302-305.

[4]Balalem A，Ali A R，Amari S，et al.Ealization of a triplemode bandpass filter using a square-loop resonator[J].in IEEE MTT-SInt.Dig.， Jun，2009:849-852.

[5]KunnthphongSrisathit， ApisakWorapishet， WanlopSurakampontorn.Design of triple-mode ring resonator for wideband microstrip bandpass filters[J].IEEE Trans.Microwave Theoryand Techniques，2010，58（11）:2867-2877.

[6]Garcia-Garcia J，Bonache J，Martin F.Application of electromagneticbandgaps to the design of ultra-wide bandpass filters withgood out-of-band performance[J].IEEE Trans.Microw.Theory Tech.，2006，54（12）:4136-4140.