一种提高模式匹配速度的新方法
王同军,赵培君
(信阳农林学院 河南 信阳 464000)
字符串的模式速匹配是串处理的一种很重要的运算,它一直都是计算机科学领域研究的热点问题之一。字符串的模式匹配在众多领域被广泛的应用,如:拼写检查、搜索引擎、计算机病毒特征码匹配、入侵检测、P2P应用特征识别、图像处理、数据压缩以及DNA序列匹配等,都离不开模式匹配算法[1]。
所谓模式匹配就是在大量的文本串中查找模式串(一个给定的字符串)的一个或者多个匹配的过程。对于文本串T[0,1,2…n-1,],长度为 n;模式串 P[0,1,2…m-1],长度为 m,其中m≤n。如果在文本串T中找到模式串P,则表示匹配成功否则匹配失败[2]。
单模式匹配算法主要有KMP算法、RK算法、BM算法[3]及相关改进算法等。其中,基于BM改进的BMH算法[4]、BMHS算法[5]是目前实际应用中效率较高的一类单模式匹配算法。国内外学者近年来在单模式匹配算法及其BM算法的改进研究方而取得了丰硕成果,相关论文主要以BMH和BMHS算法作为研究和实验对比分析对象。基于BMH或BMHS算法的大部分改进算法均利用各类降低匹配窗口移动次数和增加匹配窗口移动最大距离的启发式方法来改善算法效率[6]。本文从模式串首字母的唯一性及字符在模式串中出现的概率为突破点,提出了一种新的基于首字符检测的BM模式匹配改进算法。该算法吸收了BMG[7]和BMHS等相关改进算法的优点,显著提高了最大移动距离。
1 BM及其改进算法
1.1 Boyer-Moore算法分析
该算法采用了两种启发性方法[8]:“坏字符启发性方法(Bad char)” 和“好后缀启发性方法(Good suffix)”。 在匹配过程中模式串P[0,1,2…m-1]由左向右移动,而字符的比较却自右向左进行,即按照 P[m-1],P[m-2],…,P[0]的次序进行比较,当文本中的字符与模式完全相等时,则匹配成功;若不匹配时,则根据预先定义的偏移函数Bad char和Good suffix计算出偏移量。
1)坏字符启发性方法:若匹配失败发生在T[i+j]≠P[i],且T[i+j]不出现在模式串P中,则将模式右移直到P[1]位于匹配失败位T[i+j]的右边第一为(即 T[i+j+1]);若T[i+j]在P中有若干地方出现,则应选择 i=max{k|P[k]=T[i+j],0≤k≤m-1},使得P[i]与 T[i+j]对齐。
2)好后缀启发性方法:如果在模式中P[m-j]处发现不匹配,则已有0个或多个字符后缀P[m-j+1]…P[m-1]匹配,在模式串中查找其他相同子串的位置,选取较大的一个作为滑动值。
1.2 Boyer-Mooer-Horspool算法分析
1980年,Horspool发表了改进与简化BM算法的论文,即BMH算法。该算法将失配与计算右移量独立,计算右移量先判断T[j+m-1]是否等于P[m-1],若相等则继续比较T[j+m-2]和 P[m-2],如此循环下去,直到当 T[j]=P[0]时,则发现一个成功的匹配;若中间比较到P[i]和T[i+j]发现不相等,T[i+j+1…j+m-1]已比较完毕且等于 P[i+1…m-1],则在 P[0…m-2]中看是否存在匹配字符,分两种情况:
1)若P[0…m-2]中不存在匹配字符,模式直接向右移动m位;
2)发现 P(k)=T[j+m-1](0≤k≤m-2)则,模式串右移 m-1-k位,接着继续从右向左开始新一轮的比较。
1.3 Boyer-Mooer-Horspool-Sunday算法分析
1990年,Sunday在BMH算法的基础上又提出了改进算法BMHS算法。该算法的思路是:在计算坏字符启发性方法时。根据文本串中与模式串末位对齐的字符的下一位字符的出现情况来确定移动距离。当比较进行到文本串j位置,失配发生在T[i+j]与P[i]处。只使用T[j+m]决定右移量,当下一个字符T[j+m]不在模式串中出现时。它的右移量比BMH算法的右移量大,BMHS算法右移m+1位。BMH算法只能右移Badchar[j+m-1]位置,即便是T[j+m-1]不出现在模式串中也最多移动m位。所以通常情况下,BMHS算法比BMH算法移动快,但当T[j+m-1]不出现在模式串中,而T[j+m]却出现在模式中时,即当 Badchar[j+m-1]>Badchar[j+m]时,BMHS算法的效果就不如BMH算法。
2 改进算法(BMX算法)
根据以上对BM算法匹配过程的分析,结合其他几个改进的BM算法(如BMH算法、BMHS算法)的优点,提出一种新的BMX算法。该算法主要是考虑了字符串后一位字母及模式串首字符的唯一性。通过其唯一性,使得最大位移量能够达到m+x,继而能大大提高匹配的效率。
其主要的思路是:当T[i+j]≠P[i]时,表示这一轮匹配失败,然后观察T[j+m]位在模式串中是否出现且是否唯一。
1)若T[j+m]位在模式串中出现且唯一,则按照BMG算法的结论将模式串右移m+1位;若T[j+m]在模式串中出现多次,则按照BMH算法的计算方法来确定右移量;
2)若T[j+m]位在模式串中未出现,则表明T[j+m]位与模式串中任何一位匹配都不会成功,则继续观察T[j+m+1]与P[0]是否相等;
3)若相等,则因T[j+m]不在模式串中,直接跳过该位将T[j+m+1]与P[0]对齐进行新一轮的比较,右移量为m+1位;
4)若不相等,因 T[j+m]不在模式串中出现,T[j+m+1]与P[0]不相等,表明模式串右移m+1位进行匹配也不会成功;则可继续观察 T[j+m+2]与 P[0]是否相等,重复(3)、(4)的步骤,直到匹配成功为止,其最大位移量可到达m+x。
将表1和表2对比可以看出,对于相同的字符串,BM算法匹配了7次才匹配成功,模式串的最大位移为m,且m仅出现过2次,即在整个匹配过程中,最大位移出现的概率小于百分之三十。而BMX算法只匹配了4次就能匹配成功,模式串的位移量为m+3、m+2、m+1,且出现的概率为百分之百。不难看出,BMX算法无论是在最大位移量还是在最大位移量出现的概率上,都大大优越于BM算法。

表1 BM算法移动过程Tab.1 Transformation in BM algorithm

表2 BMX算法移动过程Tab.2 Transformation in BMX algorithm
3 算法的性能测试及结果分析
本实验使用的硬件为:处理器Intel Pengtium(R)D CPU 2.80 GHz,内存 2GB,软件为Windows7 32位操作系统,Microsoft Visual C++2010集成开发环境。采用C语言编程,实验采用大小为10 MB的英文文本内容作为文本串,随机取模式串50个,长度为3-30字符,算法比较次数统计通过在程序中增加变量实现。在匹配不同长度的模式串的情况下,4种算法的字符匹配次数(见图1),完成匹配所需时间(见图2)对比测试结果如下图所示。

图1 字符匹配次数Fig.1 Number of character matching
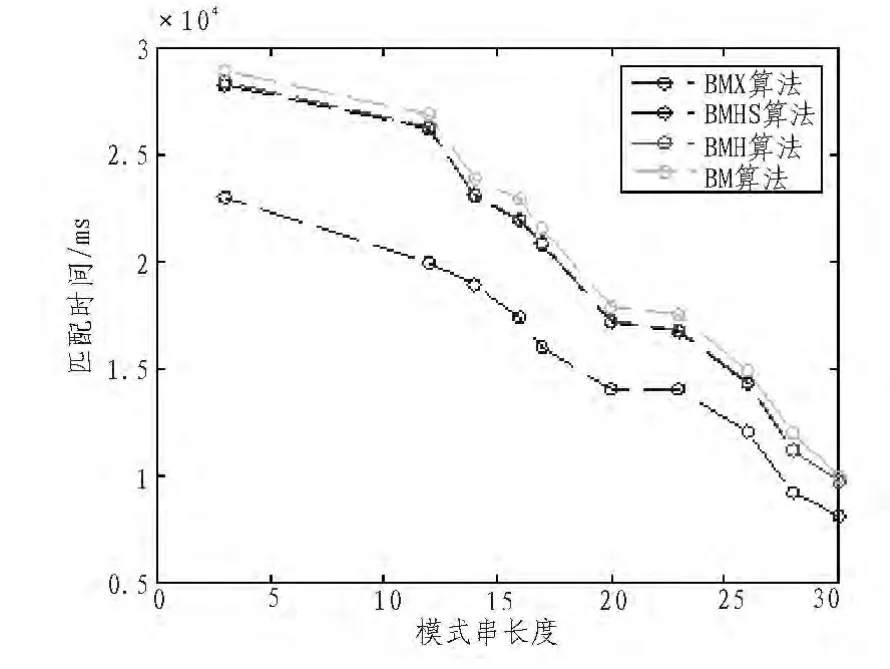
图2 完成匹配所需时间Fig.2 Time needed to complete the matching
从上述实验结果可以看出,四种算法在模式串长度一样的条件下,无论是字符的匹配次数还是完成匹配所需的时间,BMX算法的性能明显好比其他3种算要好很多。
4 结束语
模式匹配[9]算法效率高低由相关算法的移动距离来决定,本文通过对比分析BM及其改进算法的最大移动距离和匹配字符的顺序,利用坏字符和模式串首字符唯一性的特点,增大了模式串的移动距离,较低了匹配次数。通过对算法的分析和实验证明,该算法能够有效地增加模式串的右移量,大幅度提高匹配速度,降低匹配时间。
[1]王浩,张霖.基于坏字符序检测的快速模式匹配算法[J].计算机应用与软件,2012, 29(5):114-116.WANG Hao,ZHANG Lin.Quick pattern matching algorithm based on bad character sequence checking[J].Computer Applications and Software,2012,29(5):114-116.
[2]扬子江,聂瑞华.一种快速的单模式匹配算法[J].华南师范大学学报:自然科学版,2013,45(5):31-35.YANG Zi-jiang,NIE Rui-hua.A fast single-pattern match algorithm[J].Journal of South China Normal University:Natural Science Edition,2013,45(5):31-35.
[3]Boyer R S,Moore JS.A Fast String Searching Algorithm[J].Communications of the ACM,1977(20):762-772.
[4]Horspool R N.Practical Fast Searching in Strings[J].Software Practice&Experience,1980,10(6):501-506.
[5]Sunday D M.A Very Fast Substring Search Algorithm[J].Communication of the ACM,1990,33(8):132-142.
[6]王浩,张霖,张庆.基于双字符序检测的BM模式匹配改进算法[J].计算机工程与科学,2012,34(3):113-117.WANG Hao,ZHANG Lin,ZHANG Qing.An improved BM pattern matching algorithm based on double character sequence checking[J].Computer Engineering&Science,2012,34(3):113-117.
[7]张娜,张剑.一个快速的字符串模式匹配改进算法[J].微电子学与计算机,2007,24(4):102-105.ZHANG Na,ZHANG Jian.A fast improved algorithm for pattern matching in string[J].Microelectronics&Computer,2007,24(4):102-105.
[8]揣锦华,郑景,关锐.BM模式匹配算法的研究与改进[J].电子设计工程,2012,20(19):52-54.CHUAIJin-hua,ZHENGJing,GUAN Rui.Study and improve of BM pattern matching algorithms[J].Electronic Design Engineering,2012,20(19):52-54.
[9]马英辉,高磊,徐效文.基于Kalman预测和点模式匹配的多目标跟踪[J].现代电子技术,2013(14):27-30.MA Ying-hui,GAO Lei,XU Xiao-wen.Multi-object tracking based on Kalman filtering prediction and point matching algorithm[J].Modern Electronics Technique,2013(14):27-30.

