基于遗传算法解决多故障诊断问题

张舒

（西北工业大学 陕西 西安 710072）

遗传算法的设计灵感来自于大自然的进化现象。遗传算法通常用来在优化问题或分类问题中提供有效的、具有较大搜索空间的搜索机制。遗传算法运行的基本模式是，对一个由个体组成的种群，对每个个体进行评价，然后根据他们的适应度数值选择能够存活到下一代的个体，该选择过程具有随机性。然后，像在大自然中的进化一样，适应度较高的个体具有更高的存活率，也具有更大的几率进行个体的交叉和变异以产生新一代的种群。在经过连续数代进化直至种群中最佳个体的适应度不再提高时，这个最佳个体很有可能就是我们要寻求的问题的最优解[1]。

1 多故障诊断问题的背景

医学中的多故障诊断问题（Multiple Fault Diagnosis，MFD）的目的是根据病人的一系列病状来诊断出一系列病因。本文采用的数学模型是“基于概率的因果模型（Probabilistic Causal Model，PCM）”[2]。在PCM中，多故障诊断问题被归结为一个四元空间，其中，

*D是一个代表一系列病因的有限非空集合

*M是一个代表一些列病状的有限非空集合

*C是一个代表一个关系的集，它是D×M的一个子集。这个关系将病因与症状关联起来，用符号表示出来，即C中的（d，m），表示病因d可以引起症状m。

*M+是M的子集，它包含了所有显现出来的症状（即从病人身上可以观察到的症状）。需要加以说明的是，不属于集合M+的症状被认为是病人身上不具有的。

另外，一个DI是一个“诊断”，它是D的一个子集，代表引起集合M+中所有症状的所有可能的病因。DI的这个定义使它可以被表示成一个字位串，其中的每一位表示一种病因，当该位为1时表示该病因在诊断中存在，当该位为0时表示该病因在诊断中不成立。当症状集合M+中的每一个症状都与病因集合DI中的至少一个病因有一个关联C时，我们称DI“覆盖”M+。同M+一样，不属于集合DI中的病因被认为是在诊断中不成立的。

L（DI，M+）代表相对可能性，它由3个参数的乘积而决定，即 L1L2L3，其中：

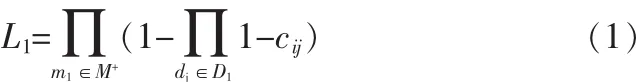
L1是DI集合中的病因引起M+中的症状的可能性。当一个诊断中不能包含M+内所有的症状时（即“非包含症状”），其L1的值为0，因此L值也为0。不幸的是，因此这个机制也否定了接下来对该非包含症状的讨论。

为了允许遗传算法能对非包含症状进行对比和讨论，我们对相对可能性做了一个微小的变化，从而使非包含症状有确切的适应度数值，而非一律为零。这个微小的变化就是将因果系数cij设定为在数值上与0或者1极为相近 （比如0.000 001或者 0.999 999），而非为0或者为1。

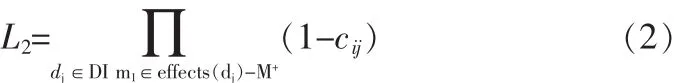
如式（2）所示，L2是DI中的病因没有引起M+之外的病状的可能性，即集合M-M+中的病状。L2是基于与DI中所有病因相关联的病状在病人身上确实存在的系数值。

L3是一个概率，它代表存在某个概率非常大（即非常常见）的病因dj在一个包含它的集合DI中起到异常大的作用的可能性。

2 遗传算法在MFD问题中的实现

在本MFD问题研究中，共有10中病状与25中可能的病因，因此对210=1 024种可能的病状组合，共有225=33 554 432种可能的病因组合。本文中只考虑1 023种病状组合，而忽略所有病状都不存在的那种情况。因此，对于遗传算法的个体表示，我们用一个10位的字位串来表示一个诊断，其中的每一位都表示一种病因。如前文所述，每一位为0或者1时分别代表该对应病因在诊断中存在或者不存在。表1中列出了本系列实验中遗传算法参数的设置。

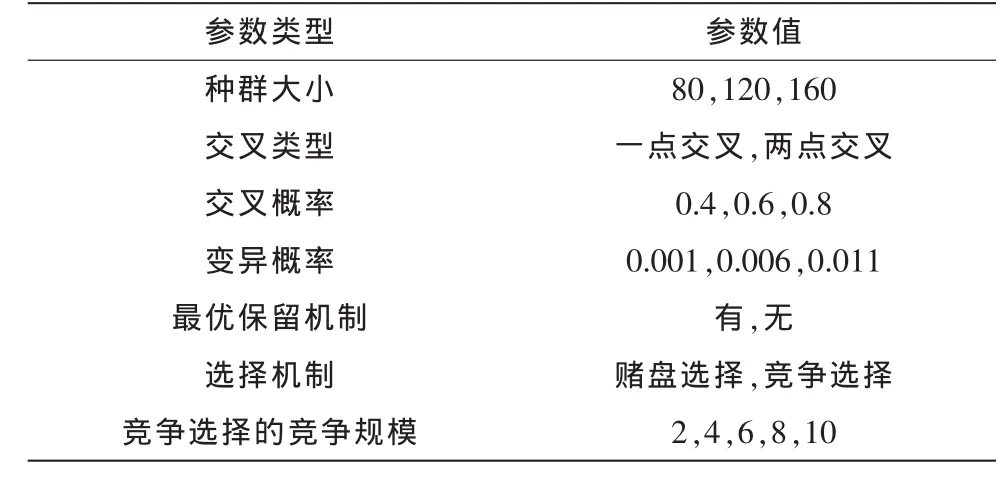
表1 遗传算法参数设置Tab.1 Experiment set up for the GA

在上述的两种选择机制中，具有较高适应度值的个体具有更高的概率被选中来产生下一代个体。在赌盘选择机制中，每个个体被选中的概率与它的适应度数值成正比[3]，如同现实中的赌盘一样，每一个区域被选中的比例与其在整个赌盘所占的面积成正比。同时，在竞争选择中，根据竞争规模大小随机选择若干个体进行适应度值比较，胜出者将被选中作为父母来产生下一代个体。

遗传算法中最重要的操作符之一是交叉操作，与现实进化中的两性交叉相对应。交叉操作最主要的两个属性是交叉类型与交叉概率。本项研究中主要探索了两类交叉操作，即一点交叉与两点交叉。一点交叉在两个作为父母的个体的同一位置选中一点，将点的同一边的基因段进行一次个体间互换，产生的两个新的个体作为子代来代替父母个体。两点交叉相当于将同样一对个体进行两次一点交叉操作，即将两个个体中分别找到对应的两个点（即一共4个点），将两点之间的对应基因段在两个个体间互换，从而产生两个新的个体作为子代[4]。

最优保留机制的原则是在子代种群中找到适应度数值最低的一个或几个，并将之替换成前一代种群中适应度数值最高的一个或几个个体。最优保留机制既有优势也有劣势，其优势为它使遗传算法记录已找到的最优个体，从而加快算法的收敛；其劣势为增加遗传算法收敛于局部最优个体的风险。因此，在本研究中对具有最优保留机制和不具有最优保留机制的两种参数配置进行了相关实验。

实验对表1所列出的参数配置选择了32种组合。针对遗传算法自身的随机性质，对于每种参数配置组合，本研究将遗传算法运行10次，因此本项研究一共运行了320次遗传算法从而得到不同的实验结果并进行相应的统计与分析。每一次运行对1023个可能的病状组合M+中的每一个进行测试，并将得出的结果与现实中的数据进行对比，从而形成一个信度测试。本文对实验结果中各种参数配置的运行结果进行了曲线比较与分析。

本系统所构建的遗传算法中关键代码如下：

Listpopulation=new List（）；

ListnewPopulation=new List（）；

for （int i=0； i

GAEntry entry=new GAEntry（）；

entry.Evaluate（entry.Similarity）；

population.Add（entry）；

}

int stable=0， count=0；

double prevBest=SaveBest（population， count， writer）；

double curBest=0；

Int limit=gaParams.IsElitism?gaParams.PopulationSize-1:gaParams.PopulationSize；

while （TermCriteria （stable， gaParams.StableGenerations，count， gaParams.Generations））{

while （newPopulation.Count

GAEntry parentA=GetParent（population， gaParams）；

GAEntry parentB=GetParent（population， gaParams）；

GAEntry child=GAEntry.GetChild（parentA， parentB，gaParams）；

child.Evaluate（child.Similarity）；

newPopulation.Add（child）；

}

if（gaParams.IsElitism）{

curBest= （from p in population select p.Fitness）.Max（）；

newPopulation.Add（（from p in population where p.Fitness==curBest select p）.ToList（）[0]）；

}

population.Clear（）；

population=newPopulation；

newPopulation=new List（）；

curBest=SaveBest（population， ++count， writer）；

if（prevBest==curBest） stable++；

else if（curBest>prevBest） {prevBest=curBest； stable=0；}

}

3 实验结果与分析

图1为两种选择机制（竞争选择和赌盘选择）的最优个体的信度曲线。从中可以看出从概率上讲，竞争选择比赌盘选择具有更高的信度，即针对MFD问题来讲，采用竞争选择的遗传算法具有更好的性能。因此我们可以分析得出，在赌盘选择中，适应度较高的个体永远比较低的个体具有更高的可能性被选中，导致搜索有可能最终收敛于局部最优个体。然而，在竞争选择中，对于竞争规模为N的遗传算法，除了整个种群中适应度最低的N-1个个体外，其他的所有个体都有机会被选中，并且其选择压力小于赌盘选择中的选择压力，因此，收敛于局部最优个体的风险被降低。

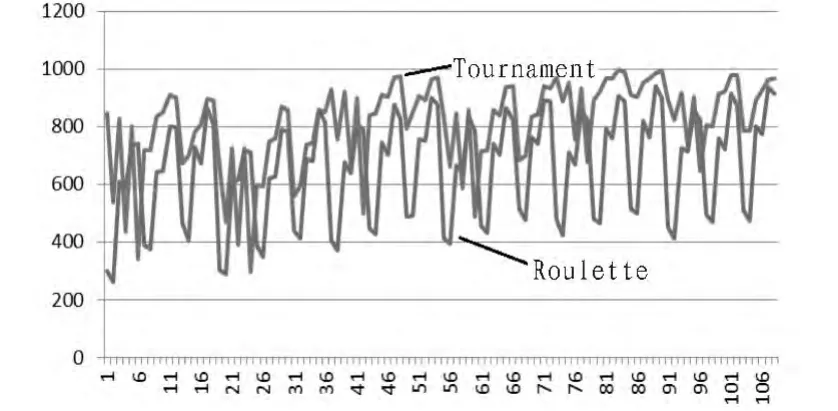
图1 不同的选择机制产生的结果比较Fig.1 Results from different selection methods

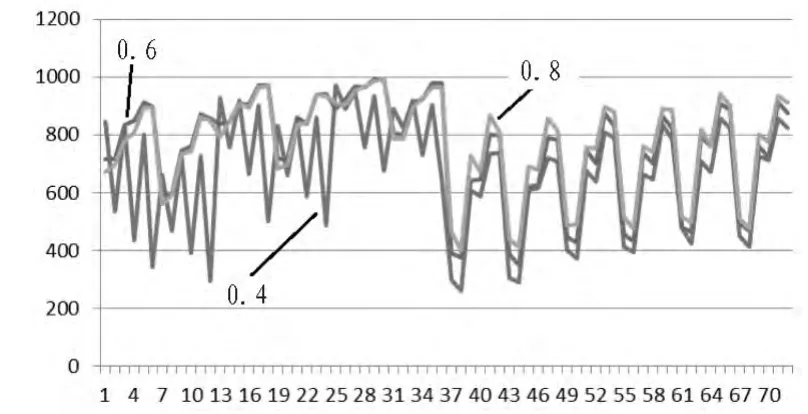
图2 不同的交叉概率所产生的结果比较Fig.2 Results from different crossover probabilities

从图2中我们可以看到较高的交叉概率导致结果中较高的信度。造成这种现象的原因是较高的交叉概率使得种群中个体具有更高的可能性来提高他们子代的适应度，从而使整个种群进化得出信度较高的个体。然而交叉概率所带来的影响在不同的选择机制下是不同的，比如在竞争选择中，遗传算法在交叉概率较低时性能下降幅度更大。

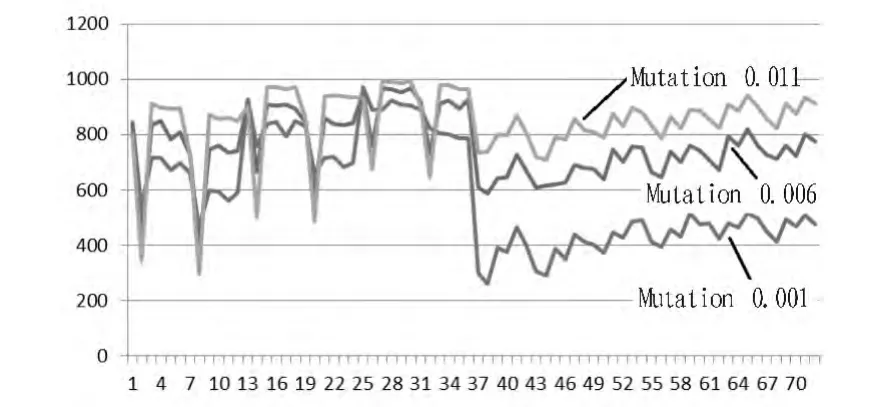
图3 不同的变异概率所产生的结果比较Fig.3 Results from different mutation probabilities

从图3中我们可以看出，在一定幅度内，变异概率越大，实验结果的信度越高。然而变异概率的影响也根据选择机制的不同而变化。在竞争选择中，随着变异概率的增大，原本产生结果信度较高的参数配置将产生信度更高的结果，原本产生结果信度较低的参数配置将产生信度更低的结果。而在赌盘选择中，产生结果的信度一直随着变异概率的增大而增高。

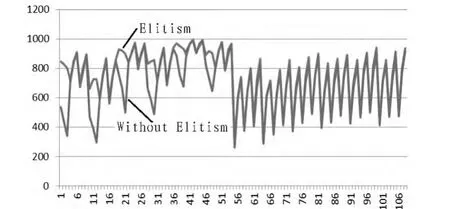
图4 有、无最佳保留机制时的结果比较Fig.4 Results with and without elitism

从图4中可以看出，当使用最优保留机制时，遗传算法可以达到更好的性能。尤其是在采用竞争选择机制的遗传算法中，最优保留机制可以大幅度降低出现低信度结果的可能性。最优保留机制可以在父代与子代之间保存适应度最高的个体的传播，以避免它在变异作用过程中消失。然而如前所述，最优保留机制不应该被盲目使用，尤其是对于保留最优个体数目较大的机制。其原因是最优保留机制常常可以造成遗传算法的提前收敛，也就是说搜索会停止在局部最优值上。

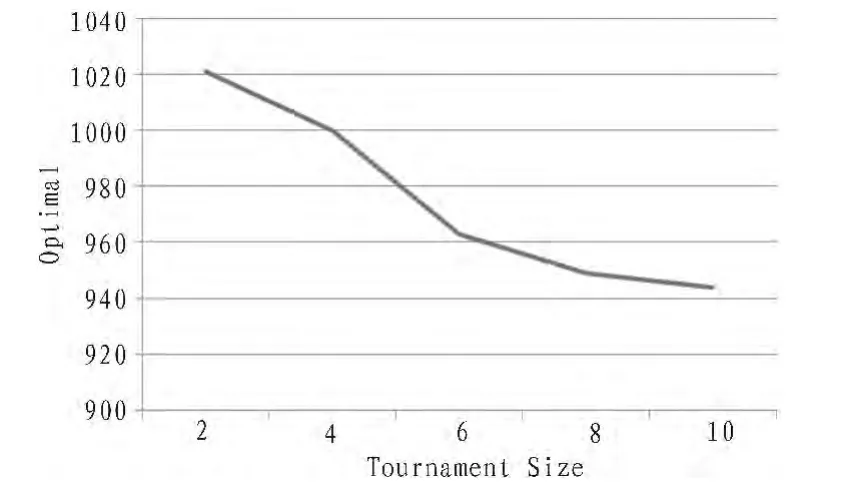
图5 不同的竞争规模所产生的结果比较Fig.5 Results of different tournament sizes

从图5中我们可以看出实验结果的信度随着竞争选择的竞争规模增大而降低。因此我们可以得出的结论是，随着竞争规模增大，选择压力增大，更多数量的低适应度个体失去被选中的机会，种群的多样性整体逐渐降低，从而会增加种群局部收敛的风险。

4 结束语

文中成功地将遗传算法应用到医学中的MFD问题中，并对遗传算法不同的参数配置产生的影响进行了比较与分析。通过实验得出，当遗传算法的参数设置控制在一定范围内时，竞争规模较小的竞争选择、概率较大的两点交叉、较高的变异率以及较大的种群数量可以获得最佳的结果。本文的研究在医学领域具有较强的实用价值，其所用技术也对遗传算法的具有良好的理论参考价值。

[1]Eberhart R，Shi Y.Computational Intelligence:Concepts to Implementations[M].Morgan Kaufmann Publisher，2009.

[2]Peng Y，Reggia J A.A Probabilistic Causal Model for Diagnostic Problem Solving Part I:Integrating Symbolic Causal Inference with Numeric Probabilistic Inference[J].IEEE Transactions on Systems， Man and Cybernetics，1987，17（2）：146-162.

[3]Potter W，Drucker E，Bettinger P.Diagnosis， Configuration，Planning，and Pathfinding:Experiments in Nature-Inspired Optimization [J].Natural Intelligence for Scheduling，Planning and Packing Problems，2009:267-294.

[4]玄光男，程润伟.遗传算法与工程优化[M].北京：清华大学出版社，2004.

[5]张莹，肖军，李天.基于遗传优化的模糊PID控制器在水加药中的应用[J].电子设计工程，2014（17）：9-12.ZHANG Ying，XIAO Jun，LI Tian.Genetic optimization of fuzzy PIDcontroller in water based dosing[J].Electronic Design Engineering，2014（17）：9-12.

[6]彭涛，周亨，邓维敏.基于GA-BP神经网络的柴油机噪声品质评价方法[J].电子设计工程，2014（17）:111-114.PENGTao，ZHOU Heng，DENG Wei-min.Diesel noise quality evaluation method based on GA-BP neural network[J].Electronic Design Engineering，2014（17）:111-114.