单级式光伏并网系统MPPT研究

薛 阳，江天博，杨骏涛，李华郁

(上海电力学院 自动化工程学院，上海 200090)

近年来，光伏发电技术得到了快速发展.如何有效地利用太阳能是各国研究的热点问题.由于光伏电池输出具有非线性特性，其输出功率受外界环境的影响.为了最大程度地利用光伏电池发出的电能，就要通过一定的控制方法保证其始终工作在最大功率点附近，以此来提高光伏电池的转换效率.目前常规的最大功率点跟踪(Maximum Power Point Tracking，MPPT)方法有定电压跟踪法、电导增量法、扰动观测法等.定电压跟踪法简单可靠，稳定性较好，缺点是不能根据外界环境的变化实现自动跟踪，常应用于功率较小、光照情况稳定的场合.传统电导增量法的优点在于跟踪性能好，但其采用固定的步长来调整工作点，步长的选择很重要，步长太大，跟踪的误差会较大，步长较小，则跟踪的速度会较慢，存在一定的缺陷.传统的扰动观察法控制简单，易于实现，是工程应用常用的算法.但初始电压的设定以及步长的选取对跟踪的速度和精度有较大的影响，有时还可能出现误判的情况.[1]

本文以传统扰动观察法为基础，提出了一种自适应的变步长扰动观察法，将其应用于5 kW单级式单相光伏并网仿真系统中.

1 光伏并网系统结构

按照功率变换的级数分类，光伏并网系统可分为单级式和多级式两种结构，其中多级式一般以两级式居多，两种光伏并网系统结构如图1所示.

图1 光伏并网系统结构

单级式并网系统中，光伏阵列直接与逆变器连接后并网，而多级式并网系统要经过一个直流/直流变换器后再接入逆变器并网.相比于多级式系统，单级式系统只有一个能量变换环节，其结构简单，使用的元器件少，可靠性高，功耗低.单级式并网系统控制时既要考虑最大功率点的跟踪控制，同时又要保证电网输出电流符合并网要求，实现起来较复杂.随着现代电力电子技术以及数字信号处理技术的发展，系统拓扑结构引起的控制困难正逐渐被克服.[2]因此，在满足系统性能要求的前提下，单级式结构将是优先考虑的一种拓扑结构.

2 MPPT算法

2.1 扰动观察法

扰动观察法是目前最常用的最大功率点跟踪算法，其基本原理为:先设定一个初始的电压值，对此时对应工作电流进行采样，求出相应的输出功率，然后对工作电压加一个扰动量，将此时的太阳能电池阵列输出功率与扰动之前的输出功率值相比，若功率比扰动之前大，则表明扰动方向正确，下一步继续朝同方向增加扰动量;若功率比扰动之前小，则表明扰动方向偏离最大功率点，下一步将朝相反方向增加扰动量.

2.2 自适应变步长扰动观察法

传统扰动观察法采用固定步长，步长的选择对于最大功率点跟踪的性能影响较大，且不适用于天气变化较快的地区.

本文提出一种变步长扰动观察法是利用功率-电压(P-U)曲线上最大功率点两侧的斜率不同来进行控制.工作点离最大功率点处越远，则|dP/dU|越大，反之亦然.利用这一特性将作为步长的变化系数来实现步长的自动调整.

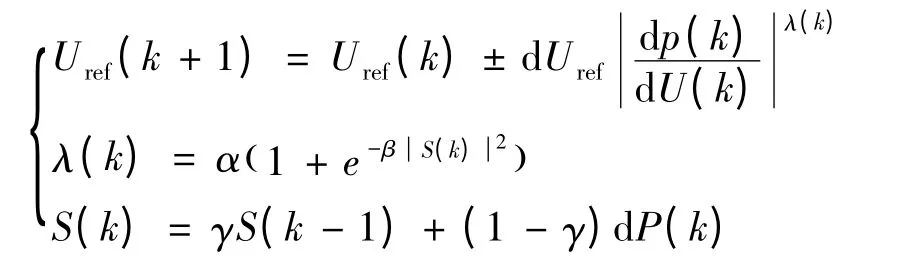
式中:Uref——参考电压;

λ(k)——增长因子;

α，β——调整因子;

S(k)——功率变化率 dp(k)的时间均值估计;

γ——遗忘因子，记录过去控制过程对现在的影响，取值范围通常在 0 ～0.1.[4]

3 仿真研究

3.1 单级式光伏并网系统的建模

在Matlab/Simulink环境下，搭建了单级式单相光伏并网系统的通用模型.仿真系统由光伏阵列、逆变电路、控制电路3个主要模块组合而成.光伏阵列模块基于光伏电池工程用数学模型搭建，[5]由42块规格型号为 STP120-12/Tb的太阳能电池串并联后构成;逆变电路采用单级式桥式逆变拓扑结构;控制电路采用电压外环加电流内环双环控制方式.

双环控制中电压外环为电流内环提供参考，电流内环要能够快速稳定地跟踪到参考信号，具体的控制过程如下:将MPPT模块的输出电压作为参考电压与光伏电池实际电压相比较，再通过PI控制器与标准正弦分量相乘得到并网电流的参考给定.参考的并网电流与实际的并网电流作差后送入PI控制器得到的值作为正弦调制波，与三角载波比较产生脉冲宽度调制信号控制逆变电路的主功率器件的导通与关断.

并网电流系统控制框图如图2所示.图2中，为参考电流信号，由直流侧电压外环提供;i为s实时的并网电流;Us电网电压;GIC(s)为PI调节环节的数学模型;GInv(s)为逆变环节的数学模型;GT(s)为滤波环节的数学模型;Gn(s)为电网电压前馈环节的数学模型;α为采样电路比例系数.

图2 并网电流控制系统

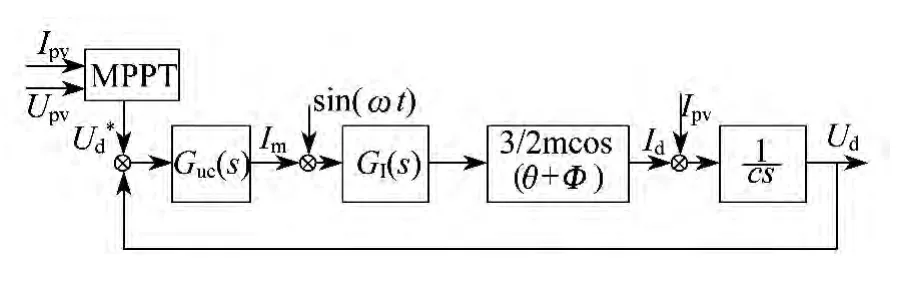
图3 直流侧电压控制系统

图4 为3个模块封装组合后的并网系统整体结构框图.此仿真系统可实时地显示电流总谐波畸变率以及系统的功率因数.

图4 并网系统整体结构

3.2 仿真结果与分析

在温度和光照强度突变条件下，将自适应变步长扰动观察法与传统扰动观察法进行对比，分析其最大功率跟踪效果以及对系统的影响，其中传统扰动观察法分小步长和大步长两种情况进行分析.以下仿真分析均采用变步长方式，选取ode23s算法.由于仿真系统较为复杂，且采用 S函数编写MPPT算法，每个步长采样时间都会计算S函数，因此实际运行时间远大于设置的仿真时间.结合实际运行情况，设置仿真时间为2 s.

3.2.1 温度突变条件下的仿真结果与分析

在光照强度不变的情况下，设初始环境温度为35℃，在t=1 s和t=1.5 s时，温度分别降至30℃和25℃，在仿真环境下用Step模块来模拟这一温度变化过程.图5给出了传统扰动观察法、自适应变步长两种算法下光伏阵列的输出电压波形.由仿真结果可知，采用两种算法都能够实现对最大功率点的跟踪.

由图5可知，温度变化时电压变化均较小，小步长扰动观察法在0.3 s左右达到最大功率点电压，曲线较平滑.大步长扰动观察法在初始阶段电压存在较大的振荡，跟踪精度较低，但在0.2 s左右电压也达到了稳定状态.相比之下，自适应变步长扰动观察法在0.1 s左右基本达到最大功率点电压，且电压较稳定，综合考虑动态及稳态特性，采用自适应变步长算法的系统性能更优.

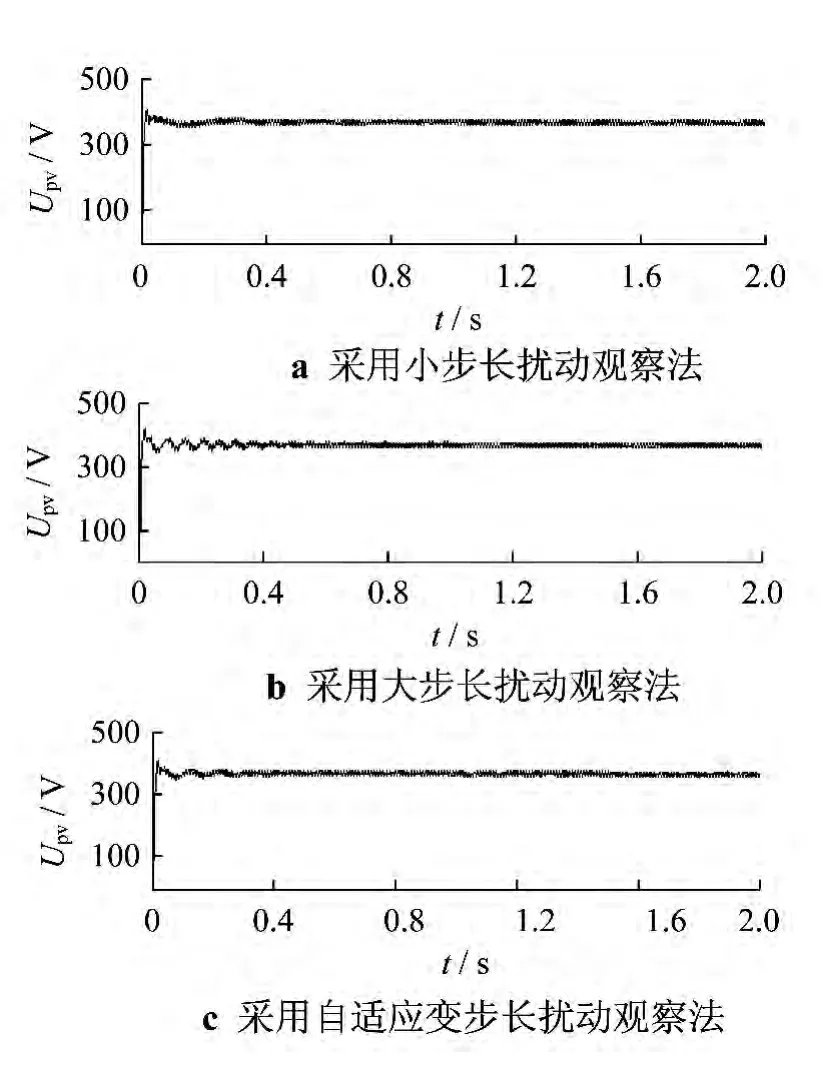
图5 光伏阵列输出电压仿真波形

3.2.2 光照强度突变条件下的仿真结果与分析

在温度不变的情况下，设初始光照强度为1 000 w/m2，在t=1 s和t=1.5 s时，光照强度分别降至900 w/m2和800 w/m2.由仿真模型中的电流畸变率和功率因数显示模块可知，采用小步长扰动观察法，在光照强度发生突变时，并网电流谐波畸变率上升，大于5%，经过较长时间后才能降至5%以下，这表明采用小步长扰动观察法的控制系统在光照强度突变的情况下，存在响应速度慢的缺点.采用大步长扰动观察法时，稳定运行后并网电流谐波畸变率为3.85%，满足并网要求，但控制精度较低.而采用自适应变步长扰动观察法时，稳定运行后并网电流的谐波畸变率为2.07%，功率因数为0.998，且在光照强度发生突变时，能够准确、快速地实现最大功率点的跟踪.

图6为光照强度突变时光伏阵列输出电压的仿真波形.由图6可知，小步长扰动观察法在光照突变后0.4 s左右达到最大功率点电压，大步长扰动观察法在光照突变时光伏阵列输出电压存在较大的振荡，0.3 s左右达到最大功率点电压.自适应变步长扰动观察法在光照突变条件下，经过0.2 s后达到了最大功率点电压，且电压波动较小.图7为光照强度突变时光伏阵列输出功率的仿真波形.

图6 光照强度突变时电压仿真波形

图7 光照强度突变时功率仿真波形

由图7进一步对比分析可知，与传统扰动观察法相比，采用自适应变步长算法在光照突变时跟踪最大功率点的效果更好.

4 结语

针对传统固定步长的扰动观察法在跟踪速度和精度方面不能同时兼顾的不足，提出了一种自适应变步长算法，并将其应用于搭建的仿真模型中.仿真结果表明，综合考虑动态及稳态特性，采用这种自适应变步长MPPT算法在外界环境突变的条件下，能够更准确、快速地实现最大功率点的跟踪，且满足并网要求.

[1]周林，武剑，栗秋华，等.光伏阵列最大功率点跟踪控制方法综述[J]. 高电压技术，2008，34(6):1 145-1 154.

[2]吴理博，赵争鸣，刘建政，等.单级式光伏并网逆变系统中的最大功率点跟踪算法稳定性研究[J].中国电机工程学报，2006，3(6):73-76.

[3]黄舒予，牟龙华，石林.自适应变步长 MPPT算法[J].电力系统及其自动化学报，2011，23(5):26-30.

[4]芮颖，牟龙华.基于自适应滤波算法的谐波仿真分析[J].电力系统及其自动化学报，2009，21(4):76-81.

[5]苏建徽，余世杰，赵为，等.硅太阳电池工程用数学模型[J].太阳能学报，2001，22(4):409-412.

[6]姚为正，芦开平，王林.单相太阳能光伏并网发电系统的仿真研究[J].电源技术，2010，34(11):1 163-1 165.