严格列对角占优矩阵‖A－1‖∞ 的上界估计

温淑鸿

(福州大学至诚学院 计算机工程系，福建 福州350002)

近些年来，国内外众多学者对于可逆矩阵‖A－1‖∞的上界估计问题一直有研究，特别是对于特殊矩阵严格行对角占优矩阵的可逆矩阵‖A－1‖∞的上界估计研究，始终是学者关注的热点。1975 年，J.M.Varah 在文献［1］中给出严格行对角占优矩阵‖A－1‖∞的一个上界估计式;2002 年王川龙和张国建在文献［2］中给出严格行对角占优矩阵‖A－1‖∞和‖A－1‖1的上界估计式;2006 年程光辉和黄廷祝在文献［3］中给出严格行对角占优M-矩阵‖A－1‖∞的上界估计式，并表明该上界比文献［1］中的好;2008 年Nenad Moraˇca 在文献［4］中给出严格行对角占优矩阵‖A－1‖1和严格列对角占优矩阵‖A－1‖∞的上界估计式。

文中主要改进了2008 年Nenad Moraˇca 在文献［4］中给出的命题2 及文中的相关结果。文献［4］命题2:设矩阵A = (aij)为n 阶M-矩阵，n ≥2，那么A－1= (bij)≥0 且

其中‖·‖表示任意矩阵范数。

1 预备知识

对文中所采用的符号及术语作一约定:字母n恒表示正整数，N = {1，2，…，n};Cm×n和Rm×n分别表示所有m × n 阶的复矩阵和实矩阵的集合;e =(1，1，…，1)T表示适当阶的所有分量全为1 的列向量，Zn= {A = (aij)∈Rn×n:aij≤0，i，j ∈N，i ≠j}。设矩阵A = (aij)∈Cm×n，A 的绝对值记为| A|，即| A| = (| aij|)∈Cm×n;A 的转置矩阵记为AT，即是把矩阵A 的行列互换所得到的矩阵，若A = (aij)∈Cn×n，A 的比较矩阵记为μ(A)= (αij)，其中

A 的极大行和矩阵范数记为‖A‖∞，即

A 的极大列和矩阵范数记为‖A‖1，即

A 的所有特征值的集合称为A 的谱，记为σ(A);A的谱半径记为ρ(A)，即ρ(A)= max{| λ |:λ ∈σ(A)};对∀i ∈N，A 的第i 行行和记为ri(A)，第i列列和记为ci(A)，即

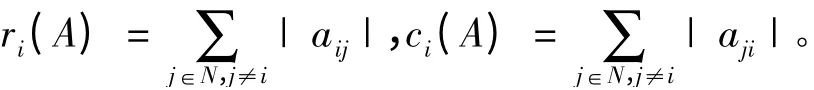
定义1［5-6］设A = (aij)∈Cn×n，如果对所有i ∈N，有| aii|≥ri(A)，则称A 为行对角占优矩阵，若AT为行对角占优矩阵，则称A 为列对角占优矩阵。定义2［5-6］设A = (aij)∈Cn×n，如果对所有i ∈N，有| aii| ＞ri(A)，则称A 为严格行对角占优矩阵，若AT为严格行对角占优矩阵，则称A 为严格列对角占优矩阵。

定义3［7］如果A ∈Zn且A－1≥0，则称A 为M-矩阵。

定义4［7］如果μ(A)为M-矩阵，则称A 为H-矩阵。

2 主要结果

引理1［1］设矩阵A = (aij)∈Rn×n，A ≥0，则

引理2［3］设矩阵A 为H-矩阵，则| A－1|≤μ(A)－1。定理3 设矩阵A = (aij)为n 阶M-矩阵，n ≥2，A－1=(bij)，则

1)H(A)≠∅，其中H(A)= {(i，j)∈N × N:| aiiajj| ＞ri(A)rj(A)，i ≠j};

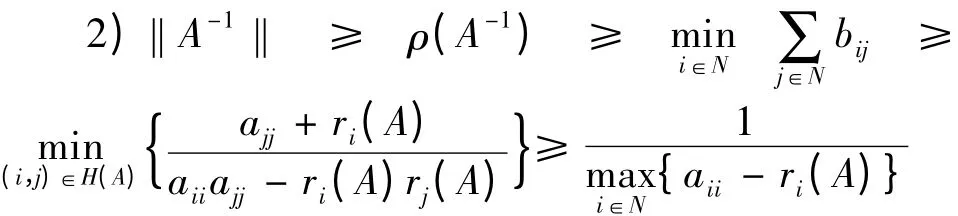
证 设A－1e = z = (z1，z2，…，zn)T，其中e = (1，…，1)T，zp= mi∈iNn{zi}，zq={zi}，由于A 为M-矩阵，故A－1≥0，那么z ＞0，根据Az = e 得

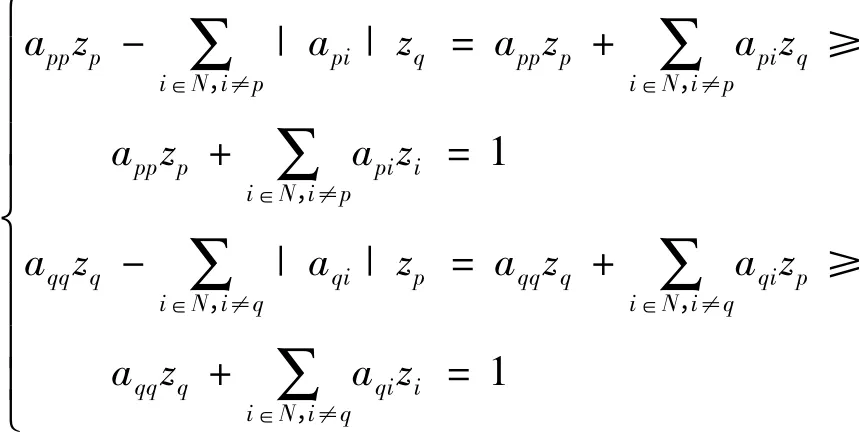
即有

由式(2)中第一个不等式知appzp≥1 + rp(A)zq，两边同时乘以aqq得

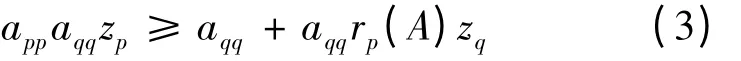
再由式(2)中第2 个不等式知aqqzq≥1 + rq(A)zp，代入式(3)有

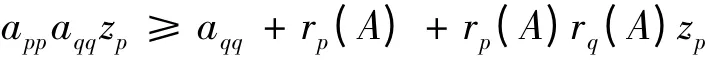
即(appaqq－ rp(A)rq(A))zp≥aqq+ rp(A)＞0，又zp＞0，可知appaqq＞rp(A)rq(A)，即(p，q)∈H(A)，因此H(A)≠∅，且有

再由引理1 有

∀(i，j)∈H(A)，若有aii－ri(A)≥ajj－rj(A)，则有aii－ ri(A)＞0，事实上，假设aii－ ri(A)≤0，则ajj－ rj(A)≤aii－ ri(A)≤0，那么aiiajj≤ri(A)rj(A)，与(i，j)∈H(A)矛盾，且有

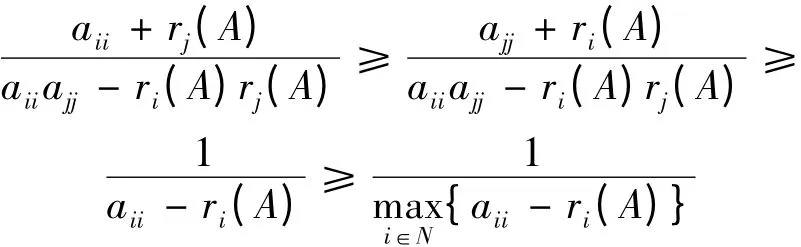
事实上

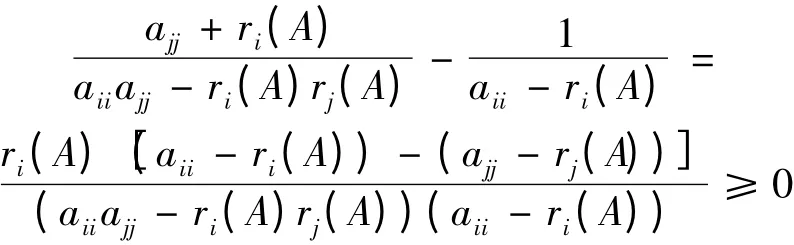
则

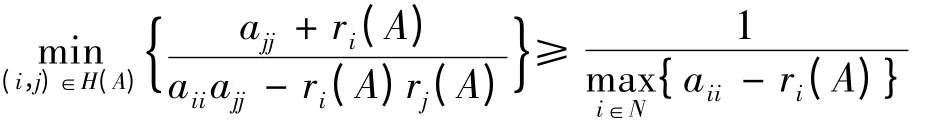
注1 可见定理3 中‖A－1‖ 的下界不小于式(1)中‖A－1‖的下界。

定理4 设a1，a2，…，an是一组复数，R1，R2，…，Rn是一组非负实数，记

若对∀i，j ∈N，i ≠j，满足| aiaj| ＞RiRj，则有

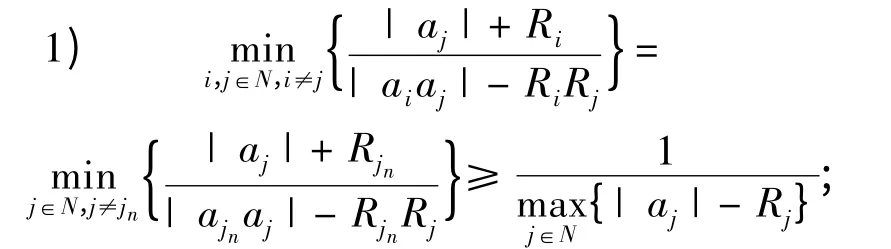
2)当J = {jn}且Rjn＞0 时，有

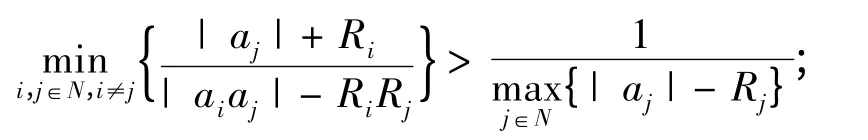
3)当J 中至少含两个元素时，有

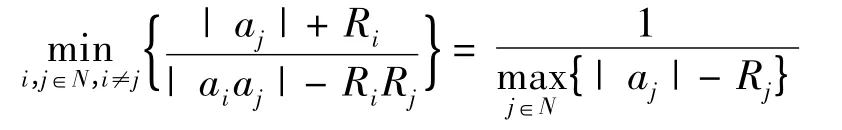
证 1)首先将实数| a1| － R1，| a2| － R2，…，| an| －Rn按从大到小的次序排列，即有1，2，…，n的一种排列j1，j2，…，jn，使得| ajn| － Rjn≥| ajn－1| －Rjn－1≥…≥| aj1| － Rj1，为叙述方便，记bk= ajk，Sk= Rjk(k = 1，2，…，n)，则有| bn| －Sn≥| bn－1| －Sn－1≥…≥| b1| － S1。

当n ＞k ＞i ≥1 时，注意到| bk| －Sk≥| bi| －Si和| bk| － Sk＞0，事实上，若| bk| － Sk≤0，则| bi| － Si≤| bk| － Sk≤0，那么| bi|| bk|≤SiSk，与条件矛盾，则有

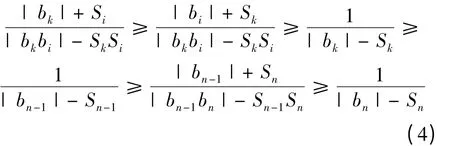
事实上

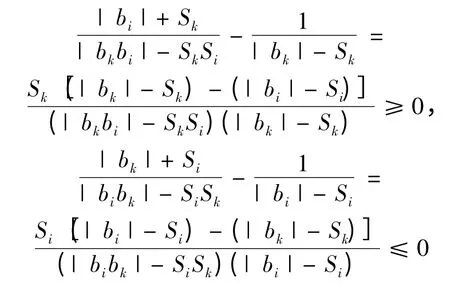
故

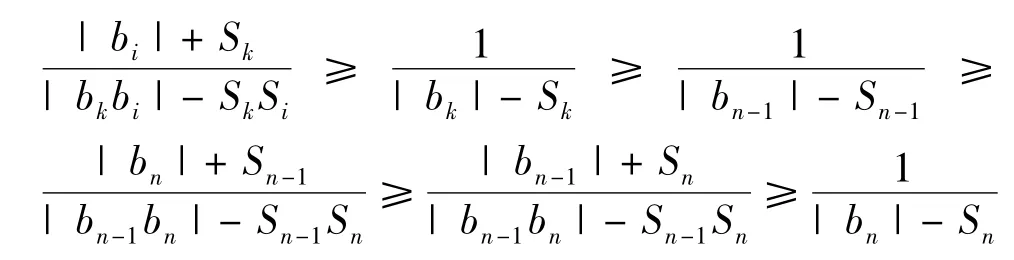
因此

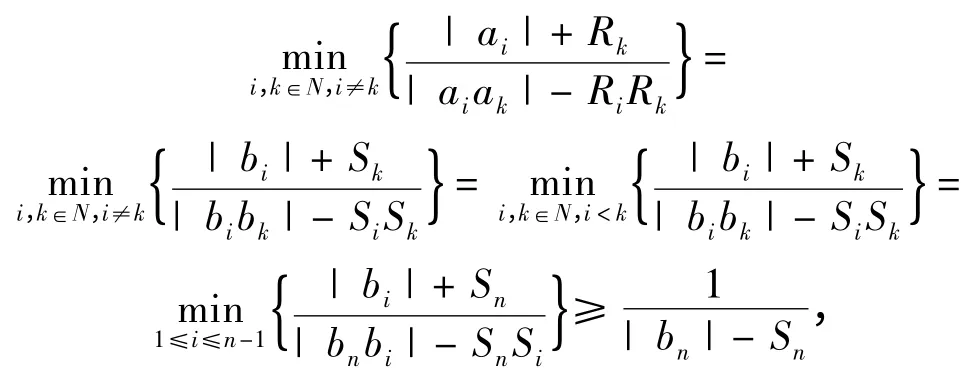
从而有

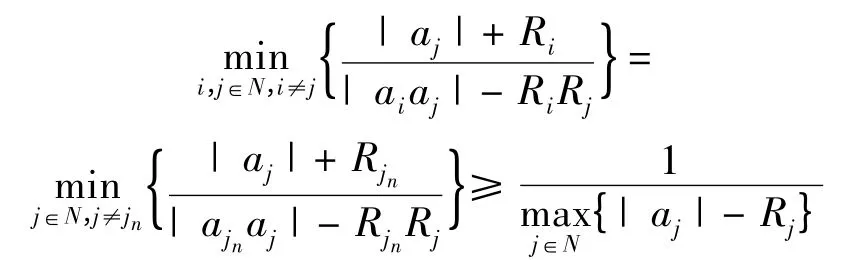
2)当J = {jn}，且Rjn＞0 时，即Sn＞0 时，∀k ∈N，1 ≤k ≤n －1，有

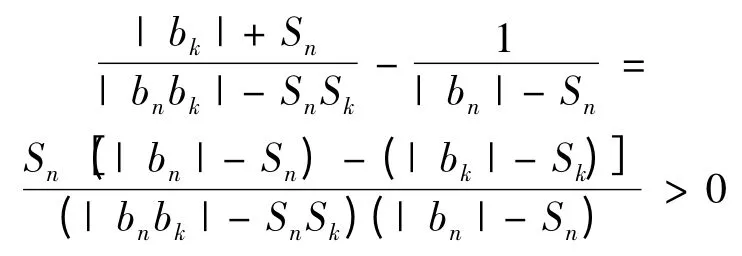
从而

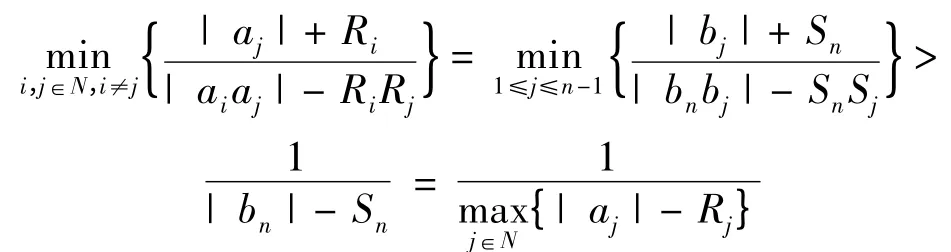
3)当J 中至少含两个元素，则必有{jn，jn－1}⊆J，这时有| bn| － Sn=| bn－1| － Sn－1，由式(4)可得

据此得

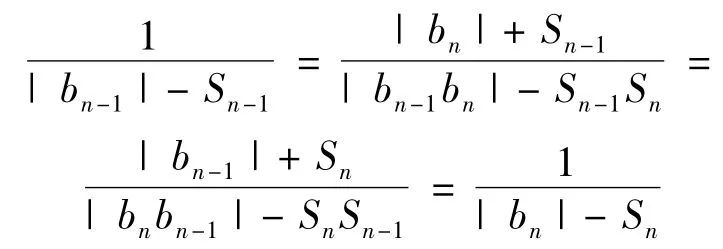
当1 ≤j ≤n －1 时，由式(4)有

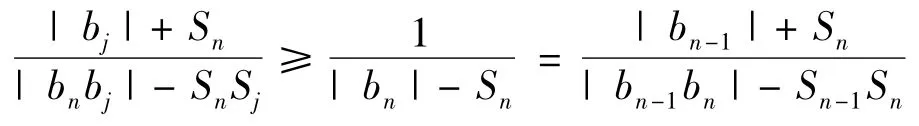
故

从而

注2 定理3 中‖A－1‖的下界可以根据定理4 来简化。

推论5 设矩阵A = (aij)为n 阶M －矩阵，n ≥2，那么

推论6 设矩阵A = (aij)为n 阶M －矩阵，n ≥2，A－1= (bij)，那么

证 由文献［5-6］知，ρ(A)= ρ(AT)，(A－1)T=(AT)－1，ri(AT)= ci(A)，矩阵A 是M － 矩阵当且仅当矩阵AT是M － 矩阵，再根据引理1，有

推论7 设矩阵A = (aij)为n 阶M －矩阵，n ≥2，那么

定理8 设矩阵A = (aij)∈Cn×n为严格行对角占优矩阵，n ≥2，那么

证 严格行对角占优矩阵为H－矩阵，由引理2 知，| A－1|≤μ(A)－1，则‖A－1‖1≤‖μ(A)－1‖1，所以不妨设A 为严格行对角占优M － 矩阵，这时A－1=(bij)≥0，由推论6 知，对所有的j ∈N，都有

设z = (z1，z2，…，zn)T，其中zi=| aii| －ri(A)，则有Ae = z，即

将式(7)展开所得n 个式子相加，可得

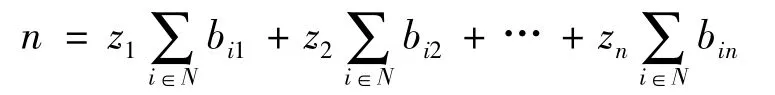
再结合式(6)，知

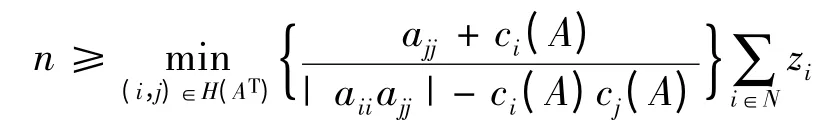
且对所有的k ∈N，有

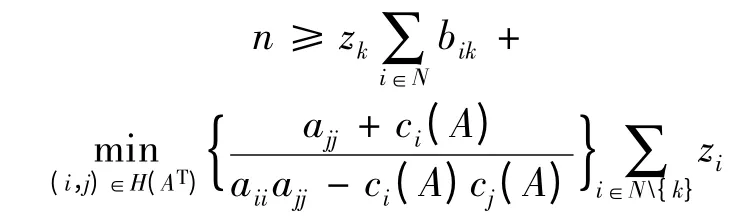
整理得

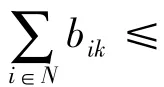
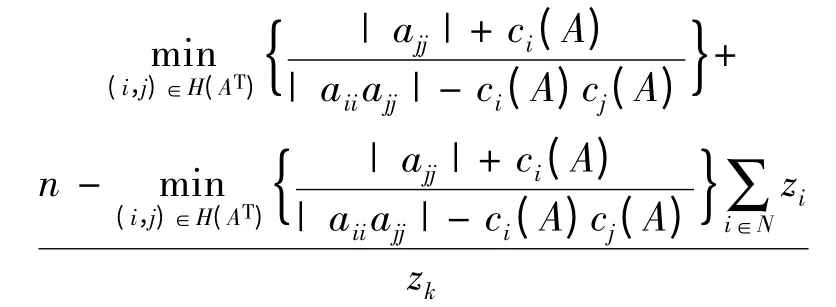
则

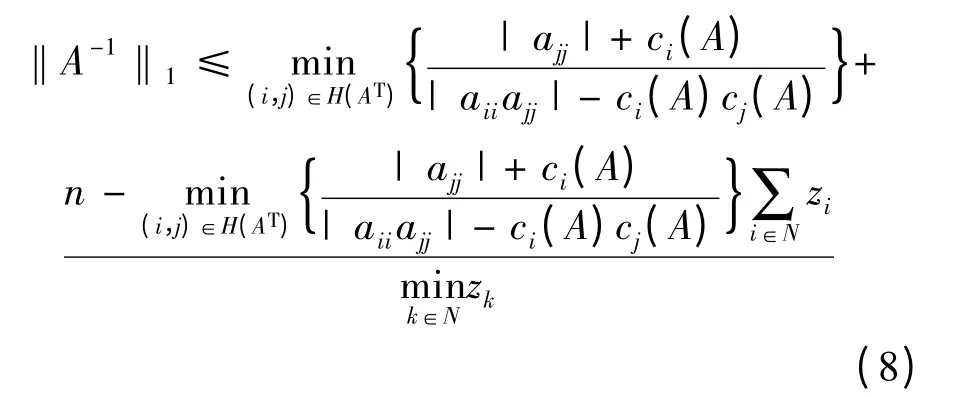
整理得式(5)。

注3 由推论6 知，式(5)中‖A－1‖1的上界不大于［4;Theorem1］中‖A－1‖1的上界。

推论9 设矩阵A = (aij)∈Cn×n为严格列对角占优矩阵，n ≥2，则

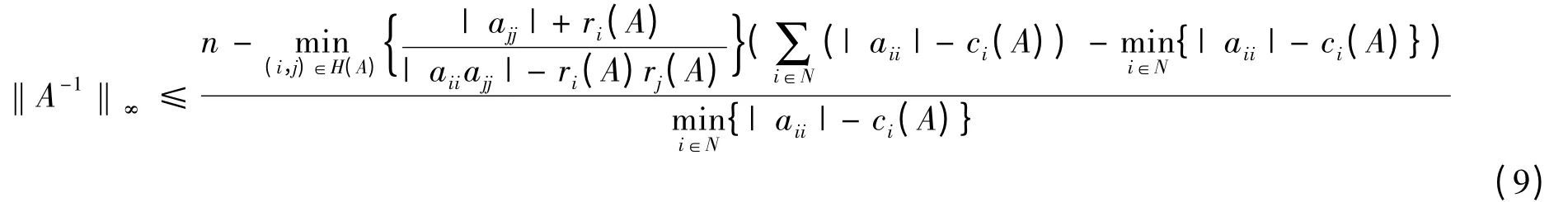
证 若A 为严格列对角占优矩阵，则AT为严格行对角占优矩阵，又‖A－1‖∞= ‖(A－1)T‖∞=‖(AT)－1‖1，对∀i ∈N，有ri(AT)= ci(A)，ci(AT)=ri(A)，再由式(8)得

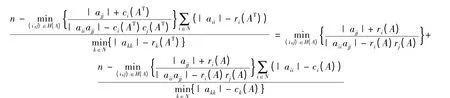
整理得式(9)。

注4 由推论5 可知，式(9)中‖A－1‖∞的上界不大于［4;Theorem2］中‖A－1‖∞的上界。

3 数值实例

本节用数值实例说明式(8)和式(9)的上界分别优于［4;Theorem1］中‖A－1‖1的上界和［4;Theorem2］中‖A－1‖∞的上界。

例1 设矩阵

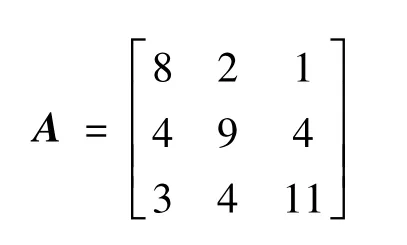
用Matlab7.0 直接计算得

利用文献［4;Theorem1］计算得‖A－1‖1≤1.5，利用式(8)计算得‖A－1‖1≤0.782 6。可以看出，定理8 中的‖A－1‖1的上界小于文献［4;Theorem1］中的上界。

例2 设矩阵

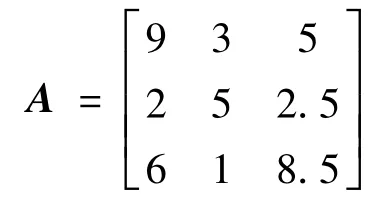
用Matlab7.0 直接计算得

利 用 文 献［4;Theorem2］ 计 算 得 ‖A－1‖∞≤1.666 7，利用式(9)计算得‖A－1‖∞≤1.390 2。可以看出，推论9 中的‖A－1‖1的上界小于文献［4;Theorem2］中的上界。

［1］Varah J M.A lower bound for the smallest singular value of a matrix［J］.Linear Algebra Appl，1975，11:3-5.

［2］WANG Chuanlong，ZHANG Guojian.Some simple estimates for the singular values of matrices［J］.Acta Mathematicae Applicatae Sinica，English Series，2002，18(1):117-122.

［3］CHENG Guanghui，HUANG Tingzhu. An upper bound for ‖A－1‖∞of strictly diagonally dominant M-matrices［J］. Linear Algebra and Its Applications，2007，426:667-673.

［4］Moraca Nenad.Bounds for norms of the matrix inverse and the smallest singular value［J］.Linear Algebra and its Applications，2008，429(10):2598-2601.

［5］Horn Roger A，Johnson Charles R.Matrix Analysis［M］.Cambridge:Cambridge University Press，1986.

［6］Horn Roger A，Johnson Charles R.Topics in Matrix Analysis［M］.Cambridge:Cambridge University Press，1991.

［7］Berman A，Plemmons R J.Nonnegative Matrices in the Mathematical Sciences［M］.New York:Academic Press，1979.