冗余驱动消除Stewart 并联机器人奇异位形
李保坤, 郭永存, 韩迎鸽, 曹 毅
(1.安徽理工大学 机械工程学院,安徽 淮南232001;2. 安徽理工大学 机械工程博士后流动站,安徽 淮南232001;3.安徽理工大学 电气与信息工程学院,安徽 淮南232001;4. 江南大学 机械工程学院,江苏 无锡214122)
六自由度Stewart 并联机器人机构由于刚度大、承载能力强以及运动精度高等特点,已被广泛应用于运动模拟器、医疗器械、工业机器人、微纳操作、力/ 力矩传感器、空间探测、并联机床等多个高精技术领域[1]。然而,在该机构的位形空间内存在大量复杂的奇异位形,机构在奇异位形附近工作时,运动学及静力学性能将会变差;另外,由于奇异位形的存在,机构的有效工作空间将进一步缩小。为进一步提高并联机器人机构的各项性能,应尽可能避开奇异位形或消除奇异位形对机构的不良影响。Nakamura Y 等[2]和Chiaverini S 等[3]从消除奇异位形对运动精度、笛卡尔刚度以及机构的动力学性能等方面进行了研究;基于反螺旋理论,郭盛等[4]提出了一种构造可避免任何可能的运动平台奇异的三自由度转动并联机构的设计方法;张彦斌[5]通过构建雅可比矩阵,利用螺旋理论,按照支路分支连接度的不同综合出具有无奇异的完全各向同性纯移动并联机构;张耀军等[6]利用Grassmann 线几何判定绳牵引平面并联机构的奇异位形,并讨论了该机构避免奇异位形的几何条件;王玉新等[7]通过研究并联机构构型分岔特性,提出了一种利用扰动函数规避并联机构转向点奇异的方法。比较常用规避奇异的有效方法通常是利用路径规划避免奇异位形,即基于任务空间计算出预期的运动轨迹,对其整个工作过程实施无奇异的路径规划,以保证机器人在整个任务操作过程中,机构不会出现奇异位形。基于运动规划方法的奇异位形规避需要掌握机构奇异轨迹在机构位形空间内的分布情况,对于六自由度Stewart 并联机构,由于其位于位形空间内的奇异位形分布极其复杂[8-9],比较难以利用运动规划法规避奇异位形。
文献[10-13]提出可采用冗余驱动的方法消除奇异位形的影响,该方法通过添加适当的冗余驱动以消除机构的所有存在的奇异点,方法实用有效。为消除奇异位对Stewart 并联机器人机构的不良影响,文中主要阐述利用冗余驱动消除Stewart 并联机器人机构的奇异位形的原理和方法,并以实例证明该方法的有效性。
1 冗余驱动的含义
冗余驱动并联机器人机构一般具有两种方式:①在保证机构自由度不变的前提下直接在原来并联机构的基础上增加驱动关节,这种方式比较简单,但是增加了机构的不对称性,影响机构的动力学性能,并且机构的运动学反解与正解会变的比较复杂。②增加一条与机构的支链完全相同的支链,并保证机构的自由度不变,然后在增加的支链中引入驱动关节,构成冗余驱动并联机构。第②种方式可以非常容易地将驱动器安装在基座上,保证机构的对称性,并能使得机构的运动学反解简单。
2 雅可比矩阵与奇异位形
未添加冗余驱动的六自由度Stewart 并联机器人的结构如图1 所示。
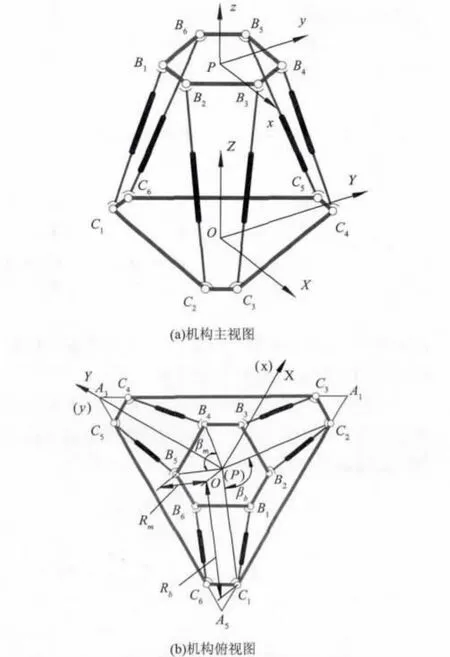
图1 Stewart 并联机器人的结构框架Fig.1 Schematic of the Stewart parallel manipulator
由图1 可以看出,其动定平台为两个非相似型的半规则正六边形B1B2…B6,C1C2…C6(i = 1,2,…,6),并通过6 根相同的球副-移动副-球副(或万向铰)支链(BiCi)相连。Bi和Ci分别为动定平台的6 个顶点,Aj(j = 1,3,5)为定平台六边形长边的交点。其中:P 为机构动平台几何中心点;O 为机构定平台几何中心点;βm为动平台上边B4B5对应中心角,0° ≤βm≤120°;βb为定平台上边C1C2对应中心角,0° ≤βb≤120°。Rm为动平台外接圆半径;Rb为定平台外接圆半径。
为分析机构的奇异位形(见图1),在动、定平台上分别建立动坐标系P-xyz 和固定坐标系O-XYZ。动平台中心点P 在固定坐标系中的位置矢量记为P,动平台上各个顶点Bi在固定坐标系中的位置矢量记为Bi(i = 1,2,…,6),在动坐标系中的位置矢量记为bi(i = 1,2,…,6),定平台各顶点Ci在固定坐标系中的位置矢量记为Ci(i = 1,2,…,6)。
根据刚体位姿变换关系不难得到

其中,R 为动平台的姿态。方程两边同时减去Ci,即可得到第i 根支链矢量表达式
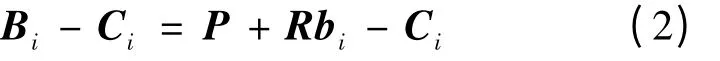
若将第i 根支链杆长记为li,则有
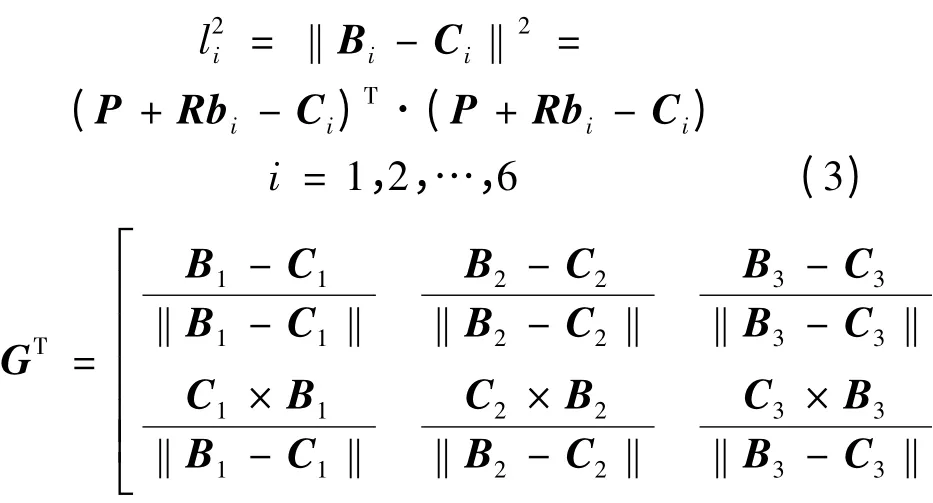
称矩阵G 为由运动输出到输入的逆速度雅可比矩阵,矩阵GT为矩阵G 的转置矩阵。
若增加一条与机构的支链完全相同的支链构建冗余驱动,则Stewart 并联机构在速度空间上描述的由运动输出到输入的逆速度雅可比矩阵为
又由文献[12]可知,Stewart 并联机器人的逆速度雅可比矩阵G 的转置矩阵GT也可表示为由关节力到操作力的线性映射,称为力雅可比矩阵GFf,即有= GT。因而,映射后的矢量长度极值可以从度量特征上评价机构的运动学和静力学性能。这些极值通常被定义为矩阵的奇异值
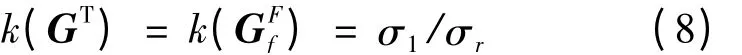
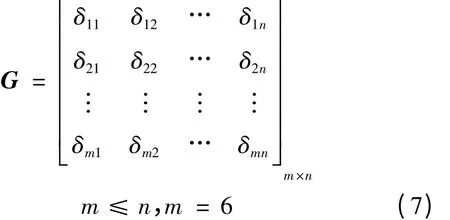
其中,σ1、σr分别为对应矩阵的最大奇异值与最小奇异值。当k =1 时,机构处于最佳的运动传递性能,称机器人机构的这一形位为各向同性。一般在机器人的机构设计时,应尽量使其条件数取较小值,从而使机器人灵巧性较高。当矩阵的条件数是无穷大即k(GT)= ∞时,机器人处于奇异位形。
若机构处于某一奇异位形时,相应的逆速度雅可比矩阵至少存在一个奇异值为0,换言之,有限的关节速度将导致操作器速度趋于无穷大。为此,通常把至少有一个奇异值为0 时的雅可比矩阵对应的式(2)两端对时间同时求一阶导数,便可得到机构基于雅可比矩阵的输入-输出运动学方程


机构的输出到输入的逆速度雅可比矩阵可以表示为

位形称为奇异位形,此时雅可比矩阵的条件数是趋于无穷大的,在物理意义上可解释为末端执行器增加了至少一个不可控的自由度[1]。
当逆速度雅可比矩阵和力雅可比矩阵至少有一个奇异值为0 时,则均为欠秩矩阵。当矩阵GFf 的奇异值均大于0 时,则为是满秩矩阵,即
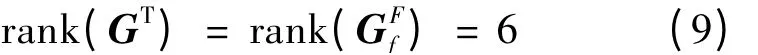
综上所述,对于Stewart 并联机构,无论是否为冗余驱动,均可通过判断逆速度雅可比矩阵的转置矩阵GT或力雅可比矩阵GFf 是否满秩判断是否处于奇异位形状态。当它们满秩时,机构不处于奇异位形;反之,则机构处于奇异位形。
3 冗余驱动消除奇异位形的方法
当Stewart 并联机构处于奇异位形时,由于6 个约束力线性相关,机构的动平台存在至少一个未被约束的剩余的瞬时自由度,机构不能保持静力学平衡,机构受力状态显著变坏。为了与动平台上很小的外力平衡,理论上需要非常大的驱动力,很容易损坏机构[1]。因此,必须避免奇异位形的产生。
以上分析可以看出,通过构造冗余驱动,使矩阵G 满足式(9),即可消除机构的奇异位形。
3.1 冗余驱动时的逆速度雅可比矩阵
当机构处于奇异位形时,rank(GT)= 6 -ε,添加ε 个冗余驱动使得rank(GT)= 6,奇异位形即可消除。根据文献[12]不难得到冗余驱动时机构的力雅可比矩阵
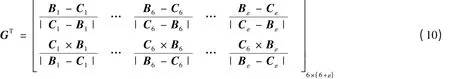
当机构为非冗余驱动时,有ε = 0,式(10)便为式(6)所示6 ×6 矩阵。
3.2 奇异位形的消除
黄真等[14]根据Grassmann 线几何将并联机器人机构的奇异位形分为一般线性丛奇异、第一类特殊线性丛奇异以及第二类特殊线性丛奇异。并指出Stewart 并联机构的奇异位形绝大多数情况属于一般线形丛奇异,即Merlet 5a[15],力雅可比矩阵GT的秩为5;而对于第一类特殊线形丛奇异,即Merlet 5b[15],力雅可比矩阵GT的秩也为5;而对于Stewart并联机构的第二类特殊线形丛奇异,只有当动、定平台重合时才会发生,此时雅可比矩阵的秩为3。
鉴于在实际应用过程中,动、定平台一般不会出现重合情况,因此,文中只探讨文献[14]所述的前两类奇异位形的消除方法,两种情况对应的机构雅可比矩阵的秩均为5。根据前面的论述,为消除这两类奇异位形,一般只需要添加一个冗余驱动支链,即式(10)中的ε = 1 即可。
4 数值实例
为进一步说明Stewart 并联机构奇异位形的消除方法,下面举例说明。
设机构的结构参数为:Rb= 20,Rm= 15 (为体现研究的一般性,结构尺寸取无量纲单位)、βb=βm=90°。现增加一个冗余驱动支链C7B7,该支链与动、定平台相连的铰链点分别是B7,C7。B7在动坐标系P-xyz 中的坐标(X'7,Y'7,0),C7在固定坐标系O-XYZ 中的坐标(X7,Y7,0),机构动平台的姿态以ZYZ-欧拉角(φ,θ,ψ)描述。
当X7= X'7= Y7= Y'7= 0,即添加的驱动支链与动、定平台铰点位于平台的几何中心点。当P 点Z坐标值一定时,非冗余驱动时的机构雅可比矩阵的条件数在给定姿态时随坐标(X,Y )变化如图2 所示。冗余驱动时的机构力雅可比矩阵的条件数在给定姿态时随坐标(X,Y )变化如图3 所示。

图2 非冗余驱动时条件数随(X,Y)的变化情况Fig.2 Condition number varies versus (X,Y)using non-redundant actuation
由图2 和图3 可以看出,非冗余驱动时机构在奇异位形与其附近处力雅可比矩阵条件数发生突变,并且机构处于奇异位形时的力雅可比矩阵条件数趋向于无穷大。增加冗余驱动后,无此现象的发生,机构运动学和静力学性能得到很大提高,有效地消除了机构原有奇异位形的不良影响。

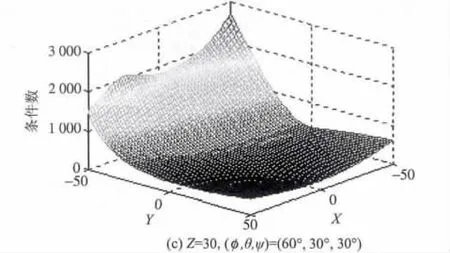
图3 冗余驱动时条件数随(X,Y)变化情况Fig.3 Condition number varies versus (X,Y)using redundant actuation
5 结 语
1)雅可比矩阵奇异值大小可以作为衡量并联机器人机构运动传递性能的一项重要指标,奇异值越大,机构运动传递性能越好,当奇异值大小为无穷大时,机构处于奇异位形状态。
2)对于Stewart 并联机器人,通过在适当的位置添加与其他支链相同结构的冗余驱动,可有效减小机构雅可比矩阵的奇异值,极大地改善了机构的运动传递性能。该方法对其他类型并联机构的奇异位形消除亦具有一定的参考价值。
3)由于Stewart 并联机器人的奇异位形绝大多数情况下为Merler 5a 类型,只需通过添加一支如2)所述的冗余驱动,即可有效消除机构的奇异位形。
4)增加冗余驱动可有效地消除并联机器人机构的奇异位形,但无疑会增加机器人控制的复杂性,因此下一步的目标将集中于冗余驱动控制并联机器人控制算法方面的研究。
[1]黄真,赵永生,赵铁石.高等空间机构学[M].北京:高等教育出版社,2006.
[2]Nakamura Y,Hanafusa H. Inverse kinematic solution with singularity robustness for robot manipulator control[J]. Journal of Dynamic System.Measurement and Control,1986,108(9):163-171.
[3]Chiaverini S,Siciliano B,Egeland O. Review of the experiments on an industrial robot manipulator[J]. IEEE Transactions on Control Systems Technology,1994,2(2):123-134.
[4]郭盛,方跃法.避免设计位形下发生平台奇异的三自由度转动并联机器人设计方法[J]. 中国机械工程,2005,16(1):8-11.
GUO Sheng,FANG Yuefa. A structural synthesis approach for 3-DOF rotational parallel manipulators avoiding platform singularities in the design configuration[J].China Mechanical Engineering,2005,16(1):8-11.(in Chinese)
[5]张彦斌,刘宏昭,胡鑫. 基于互易螺旋理论的无奇异完全各向同性移动并联机构型综合[J]. 机械工程学报,2008,44(10):83-88.
ZHANG Yanbin,LIU Hongzhao,HU Xin.Type synthesis of non-singular fully-isotropic translational parallel mechanisms based on theory of reciprocal screw[J].Journal of Mechanical Engineering,2008,44(10):83-88.(in Chinese)
[6]张耀军,张玉茹.基于Grassmann 线几何的平面柔索驱动并联机构奇异分析[J].机械工程学报,2011,47(19):1-7.
ZHANG Yaojun,ZHANG Yuru. Singularity analysis of planar cable-driven parallel mechanisms with Grassmann geometry[J].Journal of Mechanical Engineering,2011,47(19):1-7.(in Chinese)
[7]王玉新,李雨桐,潘双夏. 一种规避并联机构转向点奇异问题的新方法[J]. 中国科学E 辑:技术科学,2008,38(1):125-136.
WANG Yuxin,LI Yutong,PAN Shangxia.A novel method of turning point singularity avoidance of the parallel mechanisms[J].Science China:Technological Sciences,2008,38(1):125-136.(in Chinese)
[8]CHENG S,WU H,WANG C,et al.A novel method for singularity analysis of the 6-SPS parallel mechanisms[J].Science China:Technological Sciences,2011,54(5):1220-1227.
[9]LI B,CAO Y,ZHANG Q,et al. Position-singularity analysis of a special class of the Stewart parallel mechanisms with two dissimilar semi-symmetrical hexagons[J].Robotica,2013,31(1):123-136.
[10]LIU G F,WU Y L,WU X Z. Analysis and control of redundant parallel manipulators[C]// IEEE International Conference on Robotics and Automation.Seoul,Korea:IEEE,2001:3748-3754.
[11]杨建新,余跃庆.平面三自由度冗余并联机构的驱动奇异性分析[J].中国机械工程,2006,17(6):629-632.
YANG Jianxin,YU Yueqing.Actuator singularity analysis of planar 3-DOF redundant parallel mechanisms[J].China Mechanical Engineering,2006,17(6):629-632.(in Chinese)
[12]张彦斐,宫金良,高峰.冗余驱动消除并联机构位形奇异原理[J].中国机械工程,2006,17(5):445-448.
ZHANG Yanfei,GONG Jinliang,GAO Feng.Theory of singularity elimination by redundant actuation for parallel mechanism[J].China Mechanical Engineering,2006,17(5):445-448.(in Chinese)
[13]Saglia J A,DAI J S,Caldwell D G.Geometry and kinematic analysis of a redundantly actuated parallel mechanism that eliminates singularity and improves dexterity[J].Journal of Mechanical Design,2008,130(12):124501.
[14]HUANG Z,ZHAO Y S,WANG J,et al. Kinematic principle and geometrical condition of general-linear-complex special configuration of parallel manipulators[J].Mechanism and Machine Theory,1999,34(8):1171-1186.
[15]Merlet J P. Singular configurations of parallel manipulators and Grassmann geometry[J]. The International Journal of Robotics Reseach,1989,8(5):45-56.

