小学数学教学中错误资源的分析与应对

王倩

教学过程是学生认识和发展的过程，是学生由不懂到懂、从不会到会、从人格尚不完善到逐渐完善的过程。在这个过程中，学生说错话、做错事是正常的。课堂中学生出错也是无法避免的，错误伴随着学生的学习与成长。而且“学生的错误都是有价值的”，错误是学生最朴实的思想、最真实的经验，往往是一种鲜活而宝贵的教学资源。我们应该进一步分析学生犯错误的原因，透过错误发现有关问题，在错误上面做些文章，变“废”为“宝”，利用错误这一资源为教学服务，课堂也因错而变得更有意义和生命力。

一、“错误资源”的成因分析

1.生活经验不足产生错误

受到年龄特点和认知规律的影响，小学生缺乏足够的生活经验，对事物的认识也存在片面性，这往往会给学习带来一定的局限性，因而出现错误。如在“可能性”一课中，让学生用“一定、不可能、可能”分别说一句话，有位学生说：“孩子的身高不可能比成人高。”他还振振有词地解释：“我们的爸爸妈妈、爷爷奶奶都比我们要高。”显然，这位学生由于受到片面的生活经验的影响，产生认识上的错误。

2.思维定式产生错误

思维定式是指人们用固定的思维去分析问题和解决问题的模式。它既有正面影响，也有负面影响。在知识迁移过程中，如果受到思维定式的负面影响，学生思维受到束缚，就会产生错误。如在“求比一个数多（少）几的实际问题”一课中，学生遇“多”就“加”，遇“少”就“减”的思维定式容易造成错误。

3.新旧知识干扰产生错误

旧知识会影响新知识的学习，新知识对旧知识反过来也会产生干扰。如，在“乘法交换律、乘法结合律、乘法分配律”的教学中，用简便方法计算（10+80）×125时，有的学生会受乘法结合律的干扰，做成10+80×125;同样用简便方法计算（25×25）×4时，有的学生会受乘法分配律的干扰，做成（25×4）×（25×4）。

二、“错误资源”的应对策略

1.精心地预设错误

“认识三角形”一课中学生顺利得出：三角形两边之和大于第三边。这时我出示问题：有一个等腰三角形，其中的两条边分别为3厘米和7厘米，那么这个等腰三角形的周长是多少？学生出现两个答案：如果三角形的腰为7厘米，那么它的周长就是7×2+3=17（厘米）;如果三角形的腰为3厘米，那么它的周长就是3×2+7=13（厘米）。如我所料，学生果然会出现两个答案，此时我并不急于纠错，而是沉默不语，等待学生的反应。接着，一名学生急切地说：“如果等腰三角形的两个腰是3厘米，两腰加起来才6厘米，比第三条7厘米的边短，围不成三角形，所以答案只有一个：7×2+3=17（厘米），只有当两条短边的和大于第三条长边，才能围成三角形。”

故意让学生出错，然后让学生在错中产生质疑，在质疑中激起学生思维的火花，使学生进入深层次的思考，从而获得“柳暗花明又一村”的惊喜。其实课堂上学生出现的错误，有些是能够预料到的，这需要教师对“错误”有足够的预见性，在课堂抓住错误的契机。

2.宽容地接纳错误

在“乘法的初步认识”课上玩“拍手说算式”游戏，教师先示范拍“×× ×× ××”，生说算式3×2或2×3。接着生生互动，其中某学生拍“××× ××× ××××”，这时教师鼓励：“你没拍错，只是没拍完。能重新来一次，把它拍完吗？”该生听后自信地拍出“××× ××× ××× ×××”。接着教师追问：“她第一次拍手时，给我们提出了一个很难的问题，你们能根据她拍的情况列出与乘法有关的算式吗？”学生思考后说出3×3+1、3×2+4、4×3-2等算式。

该生的拍法显然与本节课的教学不相符，如果教师不能宽容接纳，完全忽视这一“错误”或是断然否定，该生还会勇敢、自信地举起小手吗？难得教师认可，给了该生重新拍的机会，增强其学习的信心。同时正是这一“错拍”，给同学们提供了创新思维的情境，成就了课堂的意外精彩，在原有认知的基础上又拓展了学生的认知，从而让这节课充满了张力。

3.理性地认识错误

在“8加几”一课中计算8+6=？某学生认为8+6=15，并说出理由：“昨天我们计算9+6=？时，是向6借1给9凑成10，那计算8+6=？时，也要向6借1给8凑成10，6还剩5，不就等于15吗？”教师板书出这位学生的想法，引导大家观察并说说出错的原因。该生立刻醒悟过来，并及时纠正自己的想法：“8+6=？要向6借2给8凑成10，6还剩4，应该等于14。”教师适时引导学生比较总结：计算“9加几”，要向另一个数借1凑成10;计算“8加几”，要向另一个数借2凑成10。

对于学生真实的想法，教师要认真倾听，理性地认识错误，让不同的思维在交流中碰撞，让学生及时醒悟并掌握正确的算法，让全班学生对于“凑十法”有更深刻的理解，这样的课堂才是不加修饰的原汁原味的课堂。

4.机智地筛选错误

“认数”的练习中有一题：十位上是（ ），个位上是（ ）的两位数是（ ）。一名学生说：“想怎么填都可以。”教师示意他举例说明，他一下便举了好几个例子，看似精彩的回答却隐藏着大错误，其他学生也被这突如其来的回答惊呆了。教师随即追问：“那最后一个括号里可以填多少个数呢？”经过交流学生知道因为填的必须是两位数，所以十位上不能为0。

对于这种错误，多数教师不会太在意，一般会一带而过。但这位老师意识到这个错误有着不同寻常的教学价值，随即进行机智地筛选，让全班同学共同讨论交流，在错误得以纠正的同时，使数学思维得以深入。

5.巧妙地运用错误

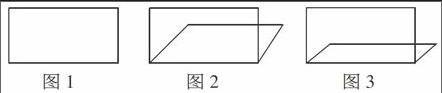
图1 图2 图3

在教学“平行四边形面积公式的推导”时，我先出示一个长方形（如图1，长7宽3），让学生说出图形名称并计算面积。再把长方形稍微一拉，成平行四边形（如图2），引出课题“平行四边形的面积”。话音未落，一位学生就高举小手说：“我知道平行四边形的面积是7×3=21，因为两条邻边还是7和3，没变！”其他学生也好像豁然开朗，都肯定是7×3=21。怎么办呢？真是急中生智：我一拉再拉，拉至上下邻边挨得更近（如图3）时问：“那照你们的想法一定还是7×3=21喽？”学生们面面相觑，还窃窃私语：“很明显图3的平行四边形的面积要比长方形的面积小很多。”“是的，接近0了呀！”学生已经发现了面积的变化，因此认识到平行四边形的面积不是两条邻边的乘积。教师顺势利导：“那平行四边形的面积该如何计算呢？你能大胆地猜测一下吗？”学生讨论后纷纷举手：“通过减拼转化成长方形就能计算出平行四边形的面积了。”

当学生试图用已有的旧知去解决新知时出现了错误，教师可通过演示给学生创造条件，让学生有足够的时间和机会去发现错误、纠正错误，学生的奇思妙想就会在教师巧妙的引导下取得意想不到的效果，增强学习的积极性和自信心。

三、小结

学生在知识建构的过程中，难免会有认识上的偏差，对于学生的错误教师要坦然面对，要让学生明白出错是正常现象。对于学生生成的错误资源，教师应迅速作出相关检索并有效分类。对于有效的错误资源，教师要让学生充分展示思维过程，显露错误资源中的闪光点，顺着学生的思路将有效成分激活，因势利导，促进学生自我反省、自我突破，使学生的好奇心和创造力在错误中发出异常的光彩。

课堂本身是丰富多彩的，错误也是其中的一部分。课堂正是因为有了错误才变得真实、鲜活;也正是因为有了错误才使学生茅塞顿开、豁然开朗。教学中我们要找出错误的原因，将错误作为一种促进学生情感和智力发展的教育资源。正确利用错误，教学的天空就不会因为学生的错误而阴云密布，拨开云雾展现的将是广阔的蔚蓝！

（责编 罗 艳）endprint