妙思巧解，演绎数学魅力

朱延春

培养学生运用数学知识解决实际问题的能力，是数学教学的目标之一。现结合“巧妙解题”的教学实录，介绍一下我是如何在解决问题的过程中，加强思维策略的指导，提升学生解决问题的策略水平的。

一、猜想——验证

自然科学，特别是数学中的新发现大都是从猜想开始的，这些猜想经过大量的时间检验，再经过严密的论证推理，才获得最终的定理、定论。在数学研究里，先猜想后证明，几乎是一条规律。教师在组织教学时，要考虑如何创设情境，为学生再发现创造必要条件。

【例1】小白兔非常爱吃青菜，兔妈妈决定在它们家门前的空地上用篱笆围一块长方形菜地，自己种菜。要想种的青菜多，围成的菜地面积就要尽量大，但自家篱笆的长度只有28米，菜地的长和宽各等于多少时，面积才能最大呢？

1.猜想——激活灵感

师：同学们，你有办法使围成的菜地面积最大吗？

生1：若长方形的长为a米，宽为b米，周长是2a+2b=28米，那么长与宽的和就是a+b=14米，长方形的面积公式是“长×宽”，我们只要求出a×b的最大积就行了。

生2：因为正方形是特殊的长方形，我们可以直接猜想“当a=b时，也就是a=b=7。a×b取得最大值”。

生3：假设a×b的最大值为7×7=49，那么长方形的最大面积为49平方米。

2.验证——得出结论

师：大家的猜想非常有道理，但究竟对不对呢？拿出纸和笔来检验一下，怎么样？

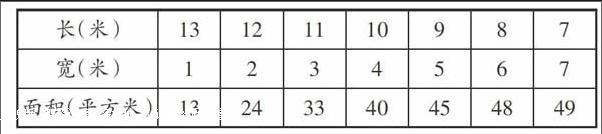
同桌交流：把长方形的长和宽变化时面积的变化情况用表格的形式表示出来：

长方形边长与面积变化规律表

[长（米）＼&13＼&12＼&11＼&10＼&9＼&8＼&7＼&宽（米）＼&1＼&2＼&3＼&4＼&5＼&6＼&7＼&面积（平方米）＼&13＼&24＼&33＼&40＼&45＼&48＼&49＼&]

生：耶！我们的猜想是正确的。

在教学中，教师要让学生在“猜想——验证”活动中感受、领悟、理解和掌握数学的思想方法，培养学生勤于思考、勇于提出猜想，并对猜想进行检验的学习态度，形成独特的个人见解，产生创新灵感。

二、探究——归纳

【例2】把、、、化成小数（除不尽的保留三位小数）。

学生顺利地把这些分数化为小数后，颇有大功告成之态。见时机成熟，我故意说：“同样是分数，为什么有的能化成有限小数，而有的却不能呢？”一石激起千重浪，学生在新问题面前个个凝神思索。这时，我启发学生仔细观察这几个分数有什么相同的地方。学生发现它们的分子都是7，我说：“对呀！为什么分子相同的有的能化成有限小数，而有的却不能呢？”把学生的思考引到对分母的观察与思考中去。他们终于发现：一个分数能否化成有限小数，跟它们的分母有关，与它们的分子无关。接着请学生将这些分数按照能否化成有限小数分成两类，比较它们的分母有什么不同。引导学生初步归纳出：一个分数，如果分母中除了2和5以外，不含有其他的质因数，这个分数就能化成有限小数，如果分母中含有2和5以外的质因数，这个分数就不能化成有限小数。

在课堂上，使学生主动地投入到知识的发生、形成、发展、运用的过程中去，切实把他们推向思考问题的最前沿，这是课堂教学中激活学生思维的重要途径。

三、数形——结合

“数”和“形”是数学中最基本的两大概念。在教学中，要有目的地帮助学生把抽象的概念、复杂的数量关系与几何图形联系起来考虑，为发展学生的直觉思维创造条件，能使题意形象具体，一目了然，从而较快地找到解题的途径。

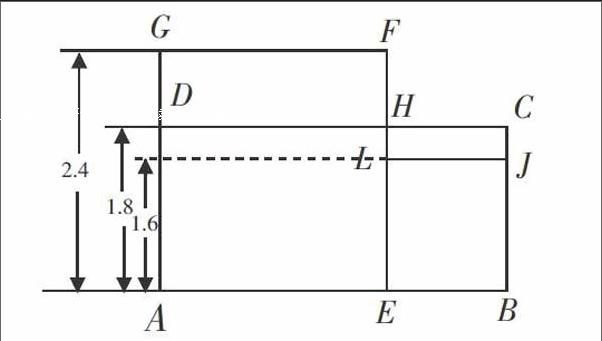
【例3】王大伯今年收获了2.4吨苹果，其中一半以上达到一级质量标准，其余达到二级质量标准。如果分等级出售，一级苹果每千克为2.4元，二级苹果每千克为1.6元;如果不分等级出售，每千克为1.8元。请你用计算器算一算，怎样出售比较合适？

解：根据题意画长方形示意图。

[A][C][B][D][F][E][G][J][L][H] [2.4][1.8][1.6]

从长方形图可见：不分等级出售，总收入为长方形ABCD的面积值。分等级出售，总收入为长方形AEFG和长方形EBJL面积和的值。需要比较长方形DHFG与长方形JLHC面积的大小，由于FH>HL，DH>HC，所以SDHFG>SJLHC。所以，分等级出售总收入更多，分等级出售更合算。

数学的思想方法是数学学科的精髓。日本著名数学家米山国藏认为：作为知识的数学出校门不到两年可能就忘了，唯有深深铭记在头脑中的数学精神、数学的思想、研究方法和着眼点等，这些随时随地发生作用，使他们受益终身。”在课堂教学中，教师要积极而又审时度势地把学生引向他们的“最近发展区”，给学生充分的独立自主学习和探究操作的活动空间，让学生在主动参与探究的过程中激活创新思维。

（责编 金 铃）endprint