追寻习题背后的精彩

顾笑颜

在小学数学学习中，练习是一个不可或缺的组成部分，新授课中有练习，练习课与复习课中更是以练习为主，练习占了整个小学数学教学时间的一半以上。因此，习题设计的好坏将直接影响学生知识掌握的质量，关系到学生思维方式的形成、学习策略的获得、数学素养的提升。而教师备课时大多比较重视新知教授阶段的设计，而将新授后的练习置于被遗忘的角落，很少用心去体会和追寻那些隐藏在习题背后的精彩。本文笔者将结合教学实际，谈谈自己对于数学习题设计的一些探索与思考。

一、找准目标，有的放矢

教学目标是教学的出发点，也是教学的归宿，支配着教学的全过程。课堂习题承载着巩固知识、训练技能的功能，要想提高课堂练习的实效，教师应紧紧围绕教学目标来设计习题。

以五年级下“圆的整理与练习”为例，学生通过前面新授知识的学习已熟记圆的周长与面积公式，在单一知识练习中也能模仿、套用公式解决一些实际问题，但一旦将周长与面积放到同一道题中，并且题目的情境再生活化一些，学生就常常对究竟求周长还是面积产生混淆。针对这一问题，笔者将这一课的教学目标之一定为：辨析周长与面积概念，灵活运用圆的周长与面积公式解决相关实际问题，并紧紧围绕“概念辨析”设计练习。

填一填：半径为2cm的圆，周长是（ ）cm，面积是（ ）cm2。

“都是12.56，这个圆的周长与面积相等吗？”“谁来在图上指一指这个圆的周长与面积？”通过两个连续追问帮助学生分辨“周长”“面积”这两个不同概念，建立概念表象。

选一选：下面哪种情况是求周长。（ ）

A.夏日中午，一棵大树投在地上的阴影是一个近似的圆形，它的半径大约是6m，阴影部分大约有多大？

B.一辆自行车的车轮外直径大约是66cm，按车轮每分钟转100圈计算，每分钟能行多远？

C.美国亚利桑那州有一个直径达1280m的巨型陨石坑，它占地多少平方米？

将问题置于选项中，引领学生拨开繁复的情境，直击问题的核心。

算一算：一只闹钟的分针长3cm，时针长2cm。这根分针的针尖1小时移动了多少厘米？时针转一圈扫过的面积是多少平方厘米？

这道对比练习意在使学生对周长、面积的理解和建构更深刻，提升学生思维的含金量。

依据教学内容，明确教学目标，抓住教学中的重难点，针对学生学习中的薄弱之处设计习题，使习题既有目的性，更有针对性;既能起到巩固知识、训练技能技巧的作用，更能促进学生数学思维的发展。

二、统整设计，增强实效

小学数学教材的编写凝聚了众多专家、学者对教育的认识、对数学的理解，其中每一道习题的安排都是有一定的目的和意图的，但是教材面对的是全体学生，因此课本习题也是最基础、最具有普适性的。这就使得教学实践中出现了两种截然不同的情况，有的教师喜欢抛开教材到课外寻找资源，认为教材中的习题过于简单、呆板。而有的教师则过度信奉教材，认为教材的安排都是好的，习惯于将课本习题原封不动地让学生一一练习。但笔者认为，两者都有不足之处。教师应该根据学生新知的掌握情况，适度地对教材中的习题进行增删、改造、统整，从而实现习题效益的最大化。

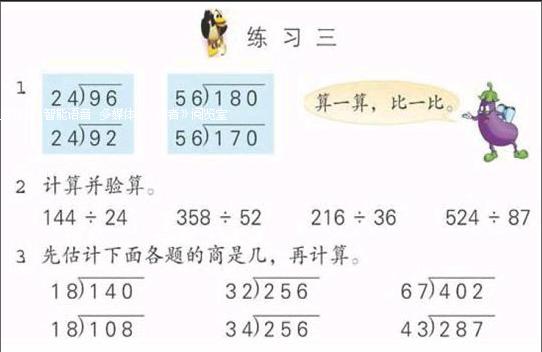
如四年级上册教材P11有这样三道习题（见下图）。

如果只是按部就班地让学生把这三题一一进行计算，课堂内的时间是不够的，学生对其中的规律还未及感悟，只有生硬接受，因此笔者将这三道习题进行了综合设计： 147÷20，147÷21，147÷29， 139÷20，并用“导学单”引领学生进行探究。

这样的调整，将零散的知识点整合于一个一以贯之的问题情境中。“比一比”，让学生体会“被除数相等时，除数越大商越小，除数越小商越大”和“除数相同时，被除数越大商越大，被除数越小商越小”这两个规律;“说一说”，帮助学生进一步巩固试商的方法及调商的基本策略;“算一算”，巩固除数是两位数除法的竖式计算和验算;“议一议”，在经验分享中回顾、整理知识结构，完善认知系统。

通过对习题的统整设计，既节约了课堂练习的时间，又将教材中习题的功能和优势发挥到了最大化，还促进了学生理解知识内涵，可谓是一举多得。

三、因材而练，引发内需

早在两千年前，至圣先师孔子就已经提出要“因材施教”。《义务教育数学课程标准（2011年版）》也在教学建议中提到，要“关注学生的个体差异，有效地实施有差异的教学”。教学要有差异，习题当然也要有差异，这样才能更好地顺应不同学生的认知需求。因此笔者认为，教师在进行习题设计时，可有意识地分成三个层次。

基础性习题：即一些基本的、简单的，难度系数等同于例题的题目，其目的是为了巩固基本概念、公式、性质、规律等，通过练习促进新知的掌握，促使知识内化。这样的练习是每个学生都要熟练掌握的。

整合性习题：即稍有变化、稍作整合，需要在对新知理解基础上再度进行分析综合才能完成，用以检查学生对新知的掌握程度和实际运用能力的习题，既利于知识的深化，又能增强学生综合应用的能力。这类习题同样要求每个学生都能掌握，但是对不同层面的学生，可有不同的要求。对于学有余力的学生要求他们能够熟练掌握，能举一反三，掌握一类题的解答方法，并能寻求多种方法来解决问题。对于学有困难的学生则要求他们能够顺利解答即可。

拓展性习题：这一层面的习题具有开放性的特点，对于学生发散思维的培养十分有利。但是并不是每一个学生都能够从中获得正向迁移的。对于那些学有困难的学生而言，过高的难度反而会让他们产生畏难的情绪，不利于学习兴趣的培养，因此这一类型的习题对他们不作要求。而学有余力的学生，特别是数学学习的优等生，则应多多鼓励他们跳一跳，采摘高处的“仙桃”。

习题有了层次，也有了弹性，学生有了选择，也有了挑战，“不同的人在练习中得到不同的发展”的目标才能得以落实。这样的分层设计，无疑是“因材施教”“有效作业”最好的注解。endprint

四、尊重主体，练中生趣

教学中，一些教师简单地认为练习的功能仅仅是“知识的巩固”与“技能的强化”，因此多有题海战术的应用。这是因为教师在教学中忽略了学生的主体地位，误以为习题的作用仅是服务于教学，而极少关注学生在练习过程中能力、情感、素养的生成和提升，缺少人文的关怀。因此笔者以为教师在设计习题时应多从练习的主体——学生考虑，习题的设计应该要让学生在练习中满足需要、升华自我。

1.变换多种形式，增加习题趣味性

小学生的年龄特点决定了他们更喜欢变化的事物。一成不变的书面练习会让他们产生“审美”疲劳。教师不妨也可以有意识地将习题的形式变一变，从而增加习题的趣味性，调动学生的积极性。

如三下“认识小数练习”一课，笔者设计了一个“比较小数大小”的习题，并将习题从书面的常规形式变化为游戏的形式。规则是：男女两队各派一名代表，每队各摸两个数，组成一个小数。比一比哪队组成的小数大。

师：女士优先，请女生先摸。

女生摸到6，师采访：你准备把6放整数部分还是小数部分？

女生：放整数部分，比6小的有6个数，比6大的只有3个数，获胜的可能性比较大。

男生摸到4，毫不犹豫放在小数部分。师：你要征求一下队友的意见吗？

男生：不用，要是放在整数部分，我们就必输无疑了，放小数部分的话，还有赢的机会。

女生摸到1。师问女生：你们希望男队摸到几？

女生：0、1、2、3、4、5。

师追问：摸6，怎么样？

女生：那我们可就输了。

男生摸到5，全体女生沸腾了。

……

每一局游戏出现的情况各不相同，学生在一次次多变的游戏中自觉应用了小数大小的比较方法，加深了对“比较小数，先比整数部分，再比小数部分”的理解，这样的设计，把学生从单调、乏味的练习中解放出来，唤起学生主动参与练习的激情，收到了事半功倍的效果。

2.激活多样生长点，触发学习动力

教学到了练习阶段，学生对一些基本的习题大多已经掌握，教师继续呈现一些传统习题，机械重复、枯燥无味根本无法吸引学生，要想让学生保持“心动”的感觉，就要在练习中给学生带来新的认识，触发学生练习的动力能源。

同样是三下“认识小数练习”一课，笔者又设计了这样一道习题：

问题一：估计一下，小芳家到学校的距离是多少千米？

问题二：小强家到学校的距离是2.5千米，指一指小强家的位置大概在哪？

问题三：根据这些信息，你能提出哪些数学问题？

本题中将估计、推测等元素巧妙地融合于实际问题中，一改“教师供给”为“学生创编”，让学生从被动的接受到主动的创造。学生根据条件“小华家距学校1.6千米”，再借助“线段图”这个半具象的支撑，估计、推测都更加有理有据，再自己提出问题并解答。如此设计练习，让习题充满生长的力量，不仅巩固了本节课的知识，更是在其中融入了估算、线段图等知识，促发了多样的生长点。

“教者若有心，学者必得益”。习题设计需要教师研读教材、了解学生、精心构思、潜心钻研，只有这样习题才能打开学生心灵的窗扉，真正与学生进行心与心的交流和碰撞。

（江苏省海门市育才小学 226100）endprint