按“四基”的要求编写数学教材

张奠宙

随着时代的进步，一些现代数学内容，逐渐进入了小学数学课程。在六年级的小学数学教材里，出现了组合数学中常用的“抽屉原理”。这是一个与时俱进的数学教学改革成果，值得肯定。但是，在如何呈现这类新内容的途径上，可以有更多的不同选择。《义务教育数学课程标准（2011年版）》突出地强调“四基”教学，即注重基本数学知识、基本数学技能、基本数学思想方法、基本数学活动经验的教学。按照这一要求，抽屉原理的教学如何设计，教材上如何表述，值得研究。

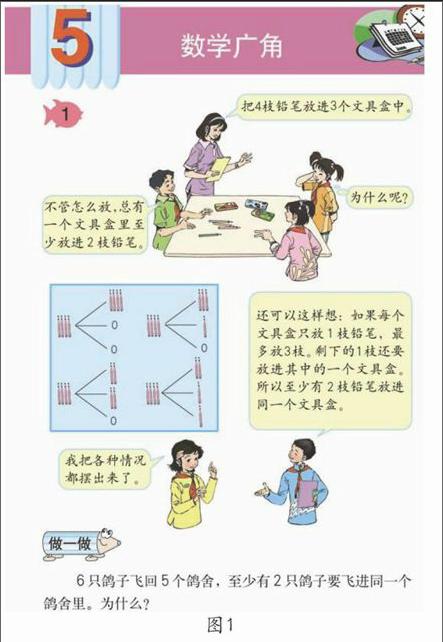
首先，在某教材六年级“数学广角”单元的第一页（图1），直接出示“文具盒放铅笔”的问题，没有用“抽屉原理”作为标题，令人遗憾。事实上，抽屉原理，或者鸽笼原理，乃是一种逻辑推理方法。它是一种普适的原理，并非单纯的个别数学问题。时至今日，它们已经成为了国际通用的名词，业已成为人们的常识。不出现“原理”二字，就将它弱化了。

其次，要研究抽屉原理教材所应表述的重点所在：究竟是当作一种“知识”进行展示呢，还是突出数学思想方法加以呈现呢？

按照现在的处理（见图1），仍然将它当作一种解题知识加以表述。思考的顺序是：

提出放铅笔问题 直接给出答案 用穷举法加以证明，最后总结为“还可以这样想……”

这里，只是把抽屉原理当作一个“问题解决”的个别例题进行呈现，因而马上给出答案。最不妥的是把穷举各种情况作为论证的基础。然而，抽屉原理并不是靠穷举各种情况再加以归纳出来的。恰恰相反，学习抽屉原理的意义在于丢开穷举检验，诉诸逻辑论证。

图1

现在，我们不妨将上述教材的呈现顺序反过来，按照“四基“的要求进行教材设计。

标题：抽屉原理

●把4个苹果放到3个抽屉里，会不会有一个抽屉里至少有2个苹果呢？

●小胖说：“我来放放看。”

●小明说：“不必一个个地放苹果，我也能断定，总有某一个抽屉里至少有2个苹果。”

●为什么呢？

●因为苹果比抽屉多一个。如果每一个抽屉里都只放1个苹果，最多放3个。那么一定多出来1个苹果。现在还要把它放到某一个抽屉里去，那么那一个抽屉就会有2个苹果了。

●小胖说：“是的，我把各种情况都摆出来了。小明的判断是对的。”

●归纳：把N个苹果放到M个抽屉里（N>M），那么一定存在某一个抽屉中至少有2个苹果。

以上的设计，突出原理的普适性，彰显逻辑推理数学方法的理性价值。

接下来，还可以进行以下的数学活动。

标题：数学活动

活动1：现在有102个苹果，要放到100个抽屉里，试问是不是一定在某个抽屉里有2个以上的苹果？来得及把所有情况都摆出来吗？怎样论证你的结论？你知道是哪一个抽屉里的苹果数大于2吗？能不能肯定该抽屉里恰好有2个苹果？

活动2：某学校有400名学生，问是否会有两个学生同一天过生日？

（分组讨论，汇报总结）[ 这是教材里的一个练习， 不妨作为课堂活动让学生讨论研究。]

这是一项非常重要的基本数学活动。事实上，活动1呈现的情况可以是成千上万的，根本无法摆完全，但是，运用抽象的演绎推理可以得出绝对肯定的结论。后面两个问题，是要说明抽屉原理是纯粹的存在性定理，只知其中有一个抽屉里至少有2个苹果，却不知道究竟是哪一个抽屉。也只知道某抽屉里的苹果数至少是2，却不能肯定究竟是几个？也许102 个苹果都放在某一个抽屉里呢！活动2是一个看起来无法回答的问题，却给出了绝对正确的答案。理性的力量令人震撼。积累这样的数学活动经验，并将之内化为一种数学思想方法，学生将终身受用。

某教材的第二页，出现了5本书放到两个抽屉的情形（图2），并引申到了7本、9本的情形。这是否有必要？放入练习如何？遗憾的是，教材呈现的情形越来越复杂，却没有展现每章蕴含的数学思想方法，制作极端情形。虽然教材的内容不可能包罗万象、面面俱到，但也不能把落实“四基”的任务统统推给任课教师。教材应该首先垂范才是。

图2

以下让我们来进行一些现代数学的注释，也许可以写入教学参考资料，供教学参考。

1.关于数学中的存在性定理和构造性定理

数学中有许多存在性的命题。它能肯定一些对象的存在，却不能具体地构造出来。最著名的是高斯首先证明的代数基本定理：在复数域内，任意单变元的N次代数方程，必有N 个根。但定理只是断言根的存在，却没有指出具体的根是什么。另一种问题则不同，比如鸡兔同笼这样的命题，不仅知道此问题一定有解，而且按照一定的方法，可以把解具体地求出来，即“构造”出来。这一类命题称为构造性的命题。中国古代数学，擅长构造性数学，善于用机械化的算法，将问题的解构造性地算出来。

2. 关于存在性数学命题的人文意境

存在性定理最美丽动人的描述，可以在中国古典诗词中获得。小学语文教材里收有贾岛的诗作《寻隐者不遇》，其中写道：

松下问童子，言师采药去。

只在此山中 云深不知处。

诗句肯定药师必定在山中，但是云深不知处。如果我们的教材里，引用这首小诗，是不是有助于对存在性命题的理解呢？是否有助于中华文化和西方数学的融合呢？教材能不能有一点创新呢？

3.初步接触逻辑量词

20世纪以来，数理逻辑迅猛发展。其中使用了两个逻辑量词，对数学教学的影响巨大。它们是：全称量词“任意一个”（传统符号是，它倒过来的字母是 A），表示单词 “all（每一个）”;存在量词的相应的符号是 ，它是反过来的字母 E，表示单词“exists（存在一个）”。抽屉原理要用到存在量词 。教材里有“总有一个“的词语，其实就是说“存在某一个”抽屉如何如何。为了传达量词的真意，和后续课程接轨，建议多用“存在某一个”的说法。存在量词的否定形式就是“全称量词”。事实上，“不存在某一个……”就意味着“任意一个都不……”这在中学数学和高等数学里使用非常频繁。

（华东师范大学数学系 200241）endprint