个数乘个数,结果怎么会等于种数?
庄治新+++严育洪


【“望”:病例观察】
“事物搭配的规律”是苏教版教材四年级下册的内容。教材例1的情境图是木偶搭配帽子——
师:小明就要过生日了,妈妈要送他一件礼物,小明来到玩具柜台旁,(出示挂图)小明要买一个木偶,再配一个帽子。像这样一个木偶配一个帽子,我们就叫搭配。柜台上有三种不同颜色的木偶和两种不同颜色的帽子,小明在思考买什么颜色的木偶配什么颜色的帽子好看,请同学们给他提些建议好吗?
师:刚才几个同学的主意都不错,那同学们能不能有序而又不重复地把所有的搭配方法都找出来,让小明自己去选择呢?请同学们拿出老师事先发给你们的木偶和帽子的图片,动手搭配一下。
反馈汇报时有两种搭配思路:A.先选帽子再配木偶;B.先选木偶再配帽子。
……
师:把木偶增加到4个,一共有多少种不同的搭配方法呢?8个、50个呢?
师:如果帽子增加到3个,又有多少种搭配方法呢?5个、100个呢?
教师根据学生的回答完成表格:
木偶个数 帽子个数 搭配种数
3 2 6
4 2 8
8 2 16
50 2 100
3 5 15
3 100 300
师:观察表格中数据,木偶的个数和帽子的个数与有多少种搭配方法之间有什么关系呢?
生:木偶个数×帽子个数=搭配种数。
师:这就是搭配的规律。
……
在练习环节,教师出示题目“如果木偶和帽子一共有12种搭配方法,那么你知道可能有多少个木偶和帽子吗?”一位学生答道:“6+6=12,……”教师未等她说完,便指着板书提醒这位学生:“木偶个数×帽子个数=搭配种数,应该从乘法上想。”谁知这位学生甚是困惑地问道:“个数乘个数,结果怎么会等于种数啊?”
【“问”:病历记录】
我们暂且不论学生“个数乘个数,结果怎么会等于种数?”这一困惑,它涉及的是教师的教法问题。笔者更多地是对这位学生“6+6=12”的回答产生好奇,隐约感觉到它的背后可能有着没有说出来的“故事”,很想知道她的答案到底是怎么来的,真的是教师所认为的对该问题尚未理解吗?
课后一问才知道,这位学生的“6+6=12”如果说完整应该是“6种+6种=12种”,于是,笔者接着追问:“如果是这样,那有多少个木偶和帽子呢?”她说出了课上没来得及说出的最终答案:“可以是2个木偶、6个帽子,也可以是6个木偶、2个帽子”。原来她是会做题的,只是不理解“个数乘个数,结果怎么会等于种数?”这一知识在形式上的矛盾,这一问题其实也就是知识的本质问题,她隐约感觉到了,只是教师没感觉到而已。
【“切”:病理诊治】
我们常说“有理走遍天下”,知识学习同样如此。学生懂“道理”,知识才会学得深刻,学得牢固,而要让学生成为得道之人,教师就必须懂得讲“道理”。上述课例中,学生的质疑“个数乘个数,结果怎么会等于种数啊?”道出了学生对知识理解的不深刻,分析教学过程,我们可以发现,学生的一知半解是因为教师教学的浅尝辄止,没有挖到知识的本质。
从教学结果上看,学生似乎根据相关条件的数据特点顺利地找到了搭配的规律——“木偶个数×帽子个数=搭配种数”,教师也似乎圆满地完成了教学任务。然而,整个教学过程,规律的得出,学生更多的是从数据的特点上找出来的,或者说是把数据“搭配”出来的,从中发现搭配的种数恰好等于木偶个数与帽子个数的乘积,并在众多例子中得到了证实。
在此值得一提的是,课中这些例子都处于同一情境中,缺乏普遍性。规律的发现与概括需要“大数据”,一是指观察素材数量足够多,二是指观察素材范围足够广,能够体现事物的多样性,所以,理想的教学是,增加其他情景,例如配衣、配餐、配人等。如教材中的“想想做做”(如下图)中线路搭配问题所呈现的就是一种很好的素材,我们可以从多方面、多角度地归纳出“一种事物个数×另一种事物个数=搭配种数”这一更抽象的规律,这样规律的得出更完整,也更可信。
不过,这些素材虽然更多地会从生活情景引入,一旦成为数学研究材料,就应该区别于生活,避免受到非数学本质因素的干扰。例如上述课例中,教师说了这么一句话——“小明在思考买什么颜色的木偶配什么颜色的帽子好看,请同学们给他提些建议好吗?”其中“好看”问题就很容易让学生陷于生活的泥潭中,对此纠缠不清。此处,教师应把问题直接指向“有多少种搭配方法”这一数学问题比较妥当。
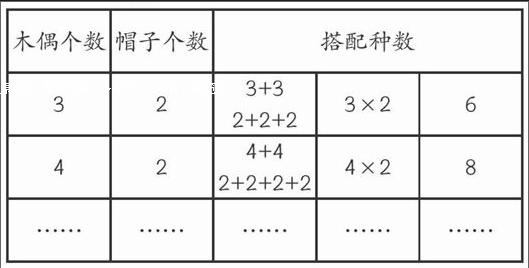
固然,本课的教学是要让学生发现数据背后隐藏的规律,从而找到一种容易操作的数学公式,便于学生运用规律去解决问题。但在得出这一算法之前,我们是否要让学生知道其中真正的算理呢?答案是肯定的,因为算法要建立在算理之上。以2个木偶与3个帽子搭配为例,如果从木偶出发,1个木偶与帽子就有3种搭配方法,那么2个木偶就有“3种+3种=6种”搭配方法,如果从帽子出发,1个帽子与木偶就有2种搭配方法,那么3个帽子就有“2种+2种+2种=6种”搭配方法,它们都可以统一用“3×2=6(种)”这一乘法算式表示。换一句话说,搭配规律的得出需要建立在“搭”与“配”的基础动作上(配合搭配动作,我们的语言可以采用“谁‘搭谁‘配成一种”这样的表述方式),也就是不仅要让学生从数据上找规律,还要让学生从活动中找规律。
教师在教学过程中如果能够从知识的本质出发,讲清上述规律中蕴含的道理,这样的教学才是建立在知识意义上的教学。在教学过程中,教师应该把算理清楚地反映出来,不能轻描淡写,我们可以把表示思路的算式补在搭配种数之前(如下表),这样就把算理固定下来,然后指导学生去寻找数据中的规律,从而发现一种简捷的解决问题的数学模型。此时,学生对“木偶个数×帽子个数=搭配种数”的理解就不会产生异议。由此可见,本课“找规律”的教学,不仅要指导学生找到知识形式上的规律,还要指导学生找到知识本质上的规律,不仅让学生找到了知识的精髓,而且事先找到了知识的精神。endprint
木偶个数 帽子个数 搭配种数
3 2 3+3
2+2+2 3×2 6
4 2 4+4
2+2+2+2 4×2 8
…… …… …… …… ……
上述课例中,那位学生“6+6=12”的回答,虽然没有一下子点到答案,但恰恰点到了知识的精神所在,也就是算理,教师不应该被表象所迷惑,误认为错。此时,教师应该耐心听学生把话说完,这样才能知道事情的真相,之后再去引导学生根据所表达的意思,把“6+6=12”转化成“2×6=12”。
上述课中,之所以学生会有此一问——“个数乘个数,结果怎么会等于种数?”还得感谢这一教材的特殊性——算法与算理不“搭配”,搭配规律的算法可以“跳过”算理,直接看事物个数就可以算出结果,正是最终在形式上算法与算理的“脱离”状态让学生在不知情的情况下触景生情,产生困惑并反映了出来,促使教师反思教学中存在的问题。
在教学中,教师把操作的目的大多定位在为了找出结果——“一共有多少种搭配方法?”至于指导学生有序搭配,也只是为了让学生能够更正确、更快速地得到搭配的结果,也就是说操作方法的有序性只是为了操作行为的有效性而为之。
虽然操作的有序性也是教师需要教会学生的一种思考方法,但在“讲道理”的知识教学中,操作的如此定位还没有实现价值的最大化。我们应该看到,有序搭配还可以让学生更容易得出反映算理“2个3种”或“3个2种”的算式“3×2”,如果教师能够看到这一操作活动所蕴藏的深意,那么学生对规律意义的深刻理解就容易水到渠成。换一句话说,教师不应该只追求“配”的结果,也应该注重“搭”的过程,从而使算法与算理能够无缝“搭配”。此时的操作就不再是为操作而操作,而是为意义而操作。
总之,学生的学习要深刻,教师的教学就要深入。教学之道不仅仅只是让学生知道走向知识的道路,还要让学生知道知识中蕴藏着的道理。学生得道了,对知识的掌握也就能够得心应手。
另外,教学之道还要让学生知道知识学习的道路,还要掌握对知识的学法。本课属于找规律的教学,那么学生就应该知道找规律的一般方法,其中以少见多、以小见大是研究问题的常规思路。由此,教师一开始就可以抛出“大数据”——成百上千个木偶搭配成百上千个帽子这样的“大问题”,让学生无从下手,自觉想到从简单问题开始研究,看一看有没有规律可循,如果有规律,是怎样的规律,从而解决问题。如果基于这样真实的科学研究设计本课,那么就能够更好地实现学生的自主学习,教学起点和教学行程都可以让学生自己确定,例如学生会从最简单的一一搭配、一二搭配、一三搭配等问题开始,发现没有研究的价值,接着就会主动增加到二二搭配、二三搭配、二四搭配以及三三搭配、三四搭配、三五搭配等,从纵横两个方向对研究素材进行不断拓展,当研究素材足够多,达到学生“满足”为止,学生就会自动转入知识的抽象概括程序,从而总结出规律。
(江苏省无锡市坊前实验小学 214111
江苏省无锡市锡山教师进修学校 214101)endprint

