超混沌系统的反同步研究

李贤丽 张超颖 窦雪莹

(东北石油大学，黑龙江 大庆 163318)

混沌运动是发生在确定的非线性系统中的一种随机行为，其对初始条件高度敏感，具有复杂的动力学性质，且难以预测，目前广泛地应用于物理学、地质学、生物学、化学及保密通信[1]等工程领域中。混沌在发现之初是用来解释某些自然和物理现象的，如蝴蝶效应及天气预报等。近年来，人们开始控制和应用混沌，混沌控制的主要方法有线性反馈法[2]、周期扰动与激励控制[3]、参数扰动法。基于混沌控制的方法，在一定条件下，构造出四维自治超混沌系统，超混沌系统与混沌系统相比具有更为复杂的动力学行为，它具有两个或两个以上正的李雅普诺夫指数，拓扑结构更为复杂，动态行为更加难以预测，更难被破解。将超混沌同步技术应用于保密通信系统时，有着更强的保密性能。混沌信号应用于保密通信是要把有用信号隐藏在混沌信号里，再在接收端提取出有用信号，可以直接利用混沌通信，也可以利用混沌同步实现通信，所以对超混沌同步方法的研究也极为重要。混沌同步是混沌控制的一种特殊形式，混沌系统的同步类型有完全同步、投影同步、反同步[4,5]及相同步[6]等，混沌同步方法有自适应同步法[7]、反馈同步法[8]、基于状态观测器广义投影同步法[9]和脉冲同步法[10]。

笔者针对超混沌liu系统，采用基于状态观测器法和反馈法设计合适的观测器和控制器，从理论分析和数值计算两个角度出发，研究超混沌系统在不同初始值条件下的反同步问题。同时，通过同步曲线和误差曲线，比较两种方法的不同之处。

1 基于状态观测器法实现反同步①

超混沌系统具有两个正的李雅普诺夫指数，与三维混沌系统相比具有更加复杂的拓扑结构，所以其动力学性质也更为复杂。笔者选取一个超混沌liu系统[11]，其系统方程为：

(1)

其中，a=35，b=35，m=2，c=2，d=10。

首先，采用基于状态观测器的方法来实现liu系统自身的反同步。把系统(1)作为驱动系统并化为f(x)=Ax+Bg(x)+G的形式。驱动系统为：

(2)

其中，A、B、G、D为定常矩阵：

G=0

根据状态观测器理论，响应系统可表示为：

(3)

响应系统中的α为投影同步中的比例系数，为了使A-BD的特征值为负实部，取特征值为(-0.5，-1，-1.5，-2)，运用极点配置法得到矩阵D：

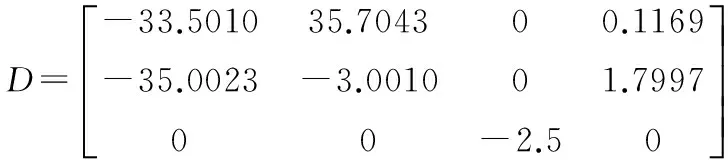
此时的响应系统为：

(4)

所谓反同步就是指混沌系统运动轨道的振幅大小相等、方向相反。因此，令比例系数α=-1，系统(1)的初始值为(2，20，35，-2)，系统(3)的初始值为(12，30，50，40)，利用Matlab进行数值仿真得到结果，此时驱动系统(1)和响应系统(3)实现了反同步，其系统的反同步曲线和反同步误差如图1、2所示。由图2可知，系统的误差e1、e2、e3、e4随着时间的增加逐渐趋于零点，也就是驱动系统和响应系统达到了反同步。

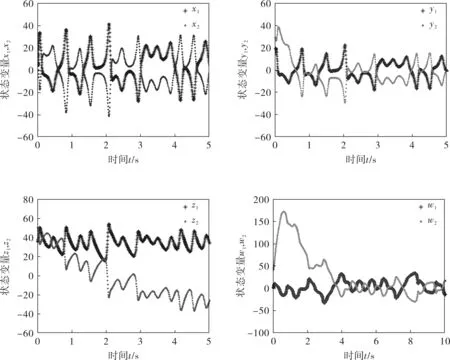
图1 驱动-响应系统中的各状态变量的反同步曲线

图2 驱动-响应系统的反同步误差曲线

2 反馈法实现反同步

同样选取系统(1)作为驱动系统，那么，其同结构加了控制器后的响应系统为：

(5)

其实U=(u1,u2,u3,u4)T即将要设计的控制器。

将系统(1)和系统(5)相加，得到误差动态系统为：

(6)

其中e1=x1+x2，e2=y1+y2，e3=z1+z2，e4=w1+w2，设计合适的控制器U=(u1,u2,u3,u4)T，将驱动系统(1)和响应系统(5)实现反同步。

以非线性控制理论为依据，设计控制器U为：

(7)

由式(6)、(7)可将误差系统转化为如下形式：

(8)

取李雅普诺夫函数为：

(9)

对式(9)取导数为：

=e1[a(e2-e1)+μ1]+e2(be1-me4+μ2)+

e3(-ce3+μ3)+e4(de2+μ4)

(10)

则可得：

令驱动系统(1)的初始值为(2，20，35，-2)，响应系统(5)的初始值为(12，30，50，40)，运用四阶Runge-Kutta法在Matlab中进行数值仿真，从而得到系统的反同步曲线和反同步误差曲线如图3、4所示。

由图2可知，当t=12.8s时，基于状态观测器法得到的同步误差曲线趋于零点。由图4可知，当t=3.0s时，反馈法得到的误差曲线趋于零点，由此可知，对于一般系统而言，采用反馈法来实现系统的同步，虽然控制器设计复杂，但是同步速度较快。

3 结束语

根据状态观测器理论和李雅普诺夫定理，采用基于状态观测器法和反馈法分别设计了观测器和控制器，对liu系统的反同步进行了理论论证，同时，利用Matlab对该系统进行数值模拟得到了系统的反同步曲线和反同步误差曲线，验证了两种方法的可行性和有效性。基于状态观测器的方法具有算法简单、计算量小的优点，与其相比，通过反馈法实现的系统同步，虽然控制器的设计较为复杂，但其同步速度相对较快，更适用于保密通信。

图3 驱动-响应系统中的各状态变量的反同步曲线

图4 系统的反同步误差曲线

[1] 李瑞红,陈为胜,李爽.超混沌Lorenz系统的投影同步及其在保密通信中的应用[J].电路与系统学报,2011,16(2):41～45.

[2] 李贤丽,王升,张秀龙,等.四翼混沌吸引子系统控制[J].大庆石油学院学报,2011,35(4):117～122，14.

[3] 李贤丽,张笑宇,王升，等.Lorenz超混沌系统的周期扰动与激励控制[J].大庆石油学院学报,2010,34(4):105～109，131.

[4] Chen J Y,Wong K W,Cheng L M,et al. A Secure Communication Scheme Based on the Phase Synchronization of Chaotic Systems[J].CHAOS,2003,13(2):508～514.

[5] 王兴元.混沌系统的同步及在保密通信中的应用[M].北京：科学出版社,2012.

[6] Tam W M,Lau F C M,Tse C K.Analysis of Bit Error rates for Multiple Access CSK and DCSK Communication Systems[J]. IEEE Transactions on Circuits and Systems I:Fundamental Theory and Applications,2003,50(5):702～707.

[7] 单梁,刘光杰,李军,等.Liu混沌系统的线性反馈和状态观测器同步[J].系统仿真学报,2007,19(6):1335～1338.

[8] Hu M F,Xu Z Y,Zhang R,et al.Adaptive Full State Hybrid Projective Synchronization of Chaotic Systems with the Same and Different Order[J].Physics Letters A, 2007,365(4):315～327.

[9] Zhang G, Liu Z R,Ma Z J.Generalized Synchronization of Different Dimensional Chaotic Dynamical Systems[J].Chaos,Solitons and Fractals,2007,32(2):773～779.

[10] 马铁东,江伟波,浮洁.基于比较系统方法的分数阶混沌系统脉冲同步控制[J].物理学报,2012,61(9)：39～44.

[11] 高智中,王颖.一个新超混沌系统及其线性反馈控制[J].数值计算与计算机应用,2012,33(3):167～172.