磁桥式磁通切换型混合励磁电机电感特性分析与建模

许泽刚，谢少军

(1.常州工学院，常州213002;2.南京航空航天大学，南京210016)

0 引 言

磁通切换型混合励磁电机［1－2］(以下简称FSHM)继承了永磁磁通切换电机的诸多优点，如转子上既无永磁体，也无绕组，机械强度高;永磁体切向安置于定子侧，易于散热和冷却，适合高速运行;聚磁效应和定子磁链双极性，有助于提升功率密度。通过引入辅助电励磁绕组，有效拓宽了永磁电机气隙磁场调节范围，在风力发电、航空航天和电动汽车等领域具有潜在的应用前景。

依据是否存在连接“C”型分瓣定子的铁心磁桥，可将FSHM 分为有磁桥［1，4，6］和无磁桥［2，3，5］两种单元结构。无导磁磁桥FSHM 具有永磁体利用率高的特点，而导磁磁桥为电励磁绕组提供了额外的并联磁分路，有助于以较小的励磁磁动势获得较大的调磁范围。

电感是反映电机静态特性的重要参数，也是建立FSHM 模型的难点和关键所在。文献［7］基于有限元法研究了无桥式FSHM 的电枢绕组电感、励磁绕组电感以及励磁绕组与电枢绕组之间的互感，鉴于电励磁磁路及电枢反应磁路经由永磁体顶部的空气磁通管闭合，因此，励磁电流及电枢电流对电感的影响相对较小。磁桥式FSHM 为兼顾永磁体利用率和电励磁调磁范围，铁心磁桥初始磁密(永磁磁动势单独作用)宜设置在铁心磁化曲线拐点的附近［8］，铁心磁桥段饱和程度的变化给电感参数的计算增加了不确定因素。

多域系统仿真软件提供了电机本体有限元模型与外电路模型的场路耦合仿真分析功能，可较为精确地研究系统性能［9－10］，但计算和存储代价相对较高，因此希望通过全系统联合仿真实现控制系统的参数整定，进而优化系统设计存在较大难度。

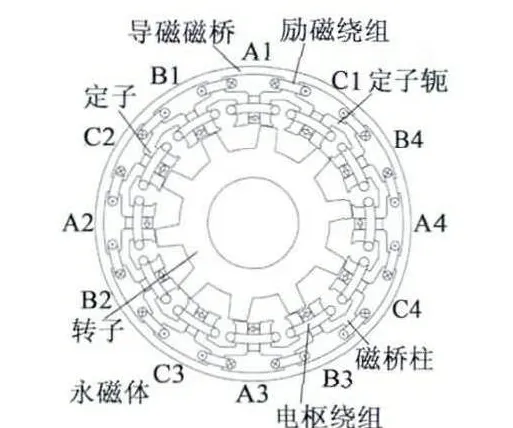
图1 三相12/10 极FSHM 电机剖面图

针对上述问题，本文以如图1所示的三相12/10极磁桥式FSHM 为例，首先建立定子坐标系下的时变电感电机模型和旋转坐标系下的交直轴电感电机模型，通过二维有限元分析得到电感随励磁电流和电枢电流变化的规律，接着利用适当的曲面拟合技术生成便于计算机快速执行的电感曲面方程。最后通过时变电感经坐标变换得到交直轴电感与旋转坐标系下的分析结果对照，以及电机外特性的仿真与实验研究，验证了磁桥式FSHM 电感分析与建模的正确性。

1 电机的数学模型

Hoang 提出永磁磁通切换电机时就将它归为永磁同步电机［11］，FSHM 虽然增加了辅助电励磁绕组，但磁链仍具有良好的正弦度［8］，因此可按正弦波电机的分析方法建立相应的数学模型。在描述和研究磁通切换电机过程中，频繁用到的是三相静止坐标系和dq 旋转坐标系。

1.1 三相静止坐标系下的电压方程

假设各相电枢绕组电阻值相等，同时忽略导体的集肤效应和温度效应，三相静止坐标系下的电压方程可表示:

式中:Rs，Rf分别为电枢绕组与励磁绕组的电阻;Ljj为各绕组的自感，Ljk为各绕组间的互感;uj和ij分别为各绕组的端电压及电流(j= a，b，c，f;k = a，b，c，f);绕组间的互感系数是可逆的，即Lab=Lba，Laf=Lfa;p 为微分算子d/dt;θe和ωe分别为转子位置电角度、转子电角速度。

1.2 dq 旋转坐标系下的电压方程

如采用坐标变换前后功率守恒的变换矩阵:

并忽略系统的不对称性以及电压、电流的零序分量，三相FSHM 在两相旋转坐标系下的电压方程可以表示为:

式中:Ld，Lq分别为电枢绕组的交直轴电感;ψm0和Lev分别为永磁空载磁链的基波幅值，相绕组与励磁绕组间互感的基波幅值。

2 三相静止坐标系下的电感特性与建模

2.1 时变电感的计算模型

以A 相为例，在电枢绕组中注入电流Ia，采用磁链法的电枢绕组自感Laa计算模型为:

式中:Nph为每相电枢绕组线圈匝数，Φa(HM，Ia=0)和Φa(HM，Ia)分别为相绕组的空载磁通，电枢磁场与永磁、电励磁磁动势共同作用下的合成磁通。

同理，与励磁电流If对应的电励磁绕组自感Lff，由A 相电枢电流产生的A 相与B 相电枢绕组之间的互感Lba，以及A 相电枢绕组与励磁绕组之间的互感Lfa可分别表示:

式中:Nf为电励磁绕组线圈匝数，Φaf(PM，If=0)和Φaf(HM，If)分别代表空载条件下励磁电流If作用前后的永磁磁通以及混合励磁磁通;Φab(HM，Ia=0)，Φab(HM，Ia)和Φaf(HM，Ia=0)，Φaf(HM，Ia)分别表示相电流Ia作用前后，B 相绕组中的空载磁通与合成磁通，以及励磁绕组中的空载磁通与合成磁通。

2.2 时变电感参数的计算与分析

永磁磁动势单独作用与额定励磁(If= ±5 A)工作状态下的空载电感曲线频谱分析结果如表1 所示。需要说明的是，为便于建模分析，表1 仅给出了对总谐波含量影响较大的最低次谐波分量。由表1可以看出，相绕组自感曲线与其互感曲线的2 倍频分量大小接近，与理想同步电机特征吻合;相绕组与励磁绕组间互感保持了良好的正弦度，表现为最低次谐波与基波分量幅值比均不超过2%。

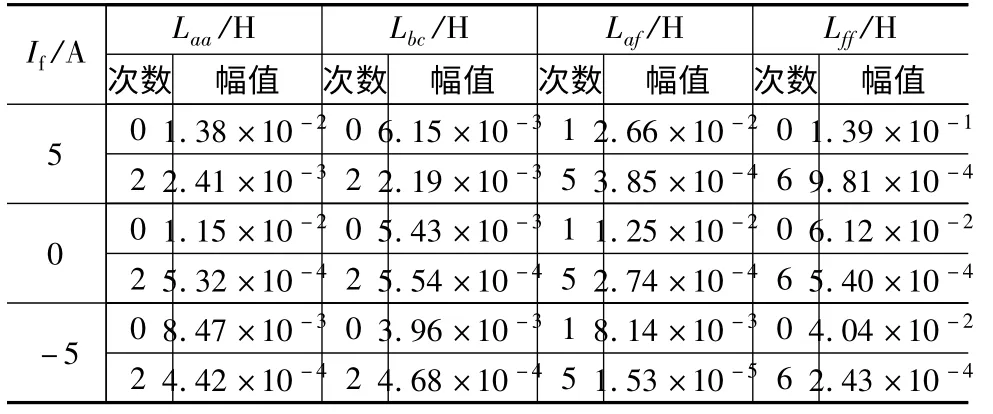
表1 自感与互感的频谱分析结果

Spline 插值法既保留了分段(低次)多项式插值的各种优点，又具有较高的预测精度［12］。图2 给出了正负额定励磁电流范围内，采用静态场分析得到的If(励磁电流)－Lev(Laf曲线基波幅值)样本数据，以及利用Spline 插值法得到的拟合曲线。在对步长为1 A 的励磁电流扫描结果进行Spline 插值时，If=4.5 A 附近出现了拐点，后经补充静态仿真数据验证了Spline 插值法预测趋势的正确性，体现了该方法对研究的指导价值。

图2 Lev与励磁电流关系曲线

插值精度与计算时间是一对矛盾，为保证电感函数的连续性，采用高阶多项式对Spline 输出数据进行拟合。鉴于Lev曲线的拟合精度是影响发电机空载反电动势、外特性仿真结果正确性的关键因素，同时为便于快速仿真，搜索发现8 次多项式的最大相对误差可接近3%，对应的拟合表达式:

为验证基于空载状态时变电感搭建的电机建模的合理性，表2 给出了上述磁桥式FSHM 在1 200 r/min，负载采用星型连接方式，分别基于式(1)所建的MATLAB 仿真模型与二维瞬态场分析得到的负载端电压。表2 显示，永磁磁动势单独作用与额定去磁工作状态(If=－5 A)下两种计算方法得到的结果基本吻合，以额定电流附近的工作点(表中以粗体示出)为例，相对误差分别仅有2. 67%和2.02%;而额定增磁工作状态(If=5 A)下的计算结果明显高于有限元仿真数据，相对误差高达11.86%，并且随负载的增加有进一步扩大的趋势。究其原因，当励磁电流较小时，磁桥段处于准饱和或深度饱和状态，因此电枢反应效果不明显;随着励磁电流的增加，磁桥段饱和程度不断较低，电枢反应去磁效果逐渐显现并导致电感值上升，由此忽略相电流对电感影响得到的负载端电压明显偏高。

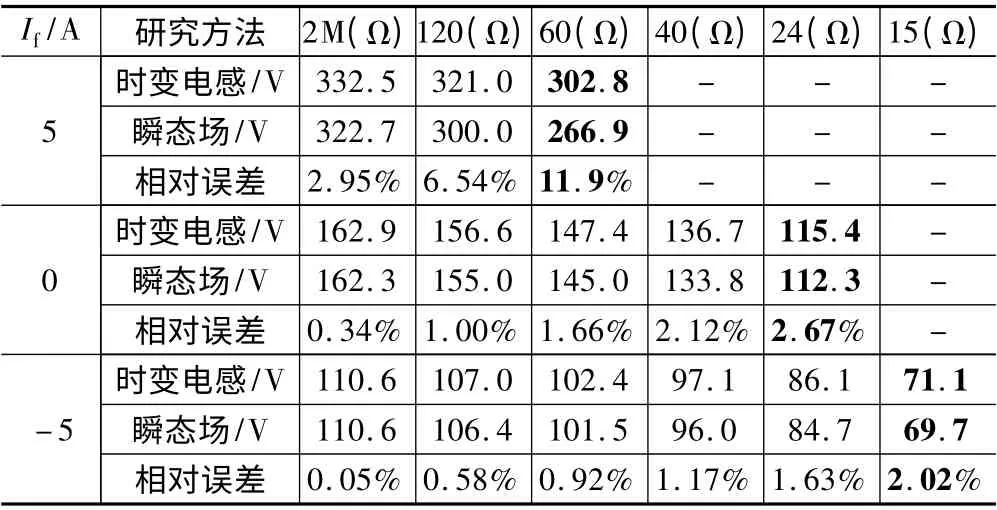
表2 时变电感建模与瞬态场计算结果对比

3 dq 旋转坐标系下的电感特性

3.1 转子坐标系下的电感计算

按照直轴电感Ld定义，依据d 轴磁动势单独作用下的d 轴磁链ψd与d 轴电流id计算求得;同理，按照交轴电感Lq定义，依据q 轴磁动势单独作用下的q 轴磁链ψq与q 轴电流iq计算求得［13］。直、交轴电感的计算公式:

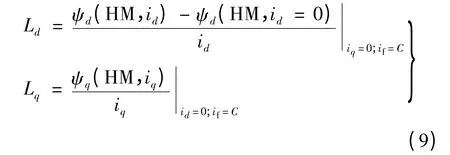
式中:ψd(HM，id=0)和ψd(HM，id)分别代表id作用前后d 轴的空载磁链以及合成磁链;ψq(HM，iq)代表永磁体与iq共同作用产生的q 轴合成磁链。

将转子旋转到d 轴轴线与A 相磁链最大位置相重合(对应θe=0°)，在相绕组中施加ia=Im，ib=ic=－Im/2，其中Im为相电流峰值。把θe=0°代入式(2)，可得:

可见，θe=0°位置只有直轴电流存在，而交轴电流为零的。此时，直轴磁链:

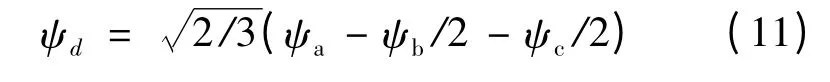
式中:三相磁链ψa，ψb，ψc可由静磁场求得。分别计算直轴电流作用前后的ψd(HM，id=0)和ψd(HM，id)，再结合式(13)即可得Ld。交轴电感的求解过程与此类似，只需将转子位置顺时针旋转机械角度9°(对应θe=－90°)。

3.2 直轴电感的分析与计算

为定性分析直轴电感Ld随励磁电流If和直轴电流Id变化的规律，图3 分别给出了直轴电感求取位置(即A 相磁链最大位置)，直轴电流单独作用、以及混合励磁去磁、永磁磁动势单独作用、混合励磁增磁工作状态下的空载磁场分布图。

图4 直轴电感的三维曲面

图3 直轴电感求取位置磁力线分布图

3.3 交轴电感的分析与计算

由图5(a)的交轴电流单独作用的磁力线分布图可知，交轴电流磁力线通路中，以虚线圈出的两处磁桥段磁力线密集，对空载电磁场影响的也更为突出。对照图5(b)、图5(c)和图5(d)发现，以虚线圈出的对应磁桥段磁力线也呈密集分布，由此Iq对Lq的影响可忽略不计。

混合励磁去磁(见图3(b))与永磁磁动势单独作用(见图3(c))模式中，以点划线圈出的区域内磁力线密集，导磁磁桥处于磁化曲线准饱和或深度饱和区(呈现高磁阻状态)，因此，Id对Ld的影响并不明显。同时，去磁工作状态磁桥部分磁力线密度高于初始值，相应Ld值更小。

若电枢绕组中通入如图3(a)所示极性的Id(对应Id正方向)，将导致以虚线圈出的图3(d)定转子齿端饱和程度降低，单就这点而言，有助于提升Ld;另一方面，因额定增磁工作模式下的磁桥段饱和程度相对较低，并且上述两图中点划线圈出区域磁通方向相反，电枢反应促使磁桥段饱和程度上升，导致Ld降低。如改变Id极性，则定转子齿端与磁桥段饱和程度的变化趋势互换。这意味着，混合励磁增磁工作模式下，Id对Ld的综合影响效果取决于各铁心单元的空载磁密及施加的直轴电流，存在不确定性。

分别改变If(－5 A≤If≤5 A)和Id(－6 A≤Id≤6 A)，其中，直轴电流扫描范围对应1.5 倍峰值电枢电流，得到如图4 所示的直轴电感三维非线性曲面。图4 显示，当If≤1 A 时，直轴电感随励磁电流的增加呈单调上升趋势，空间网格接近矩形分布，体现出直轴电感对直轴电流的变化不敏感;而当If＞1 A 时曲面形状不规整，并且曲面变化趋势与基于磁力线分布图得到的分析结果一致。

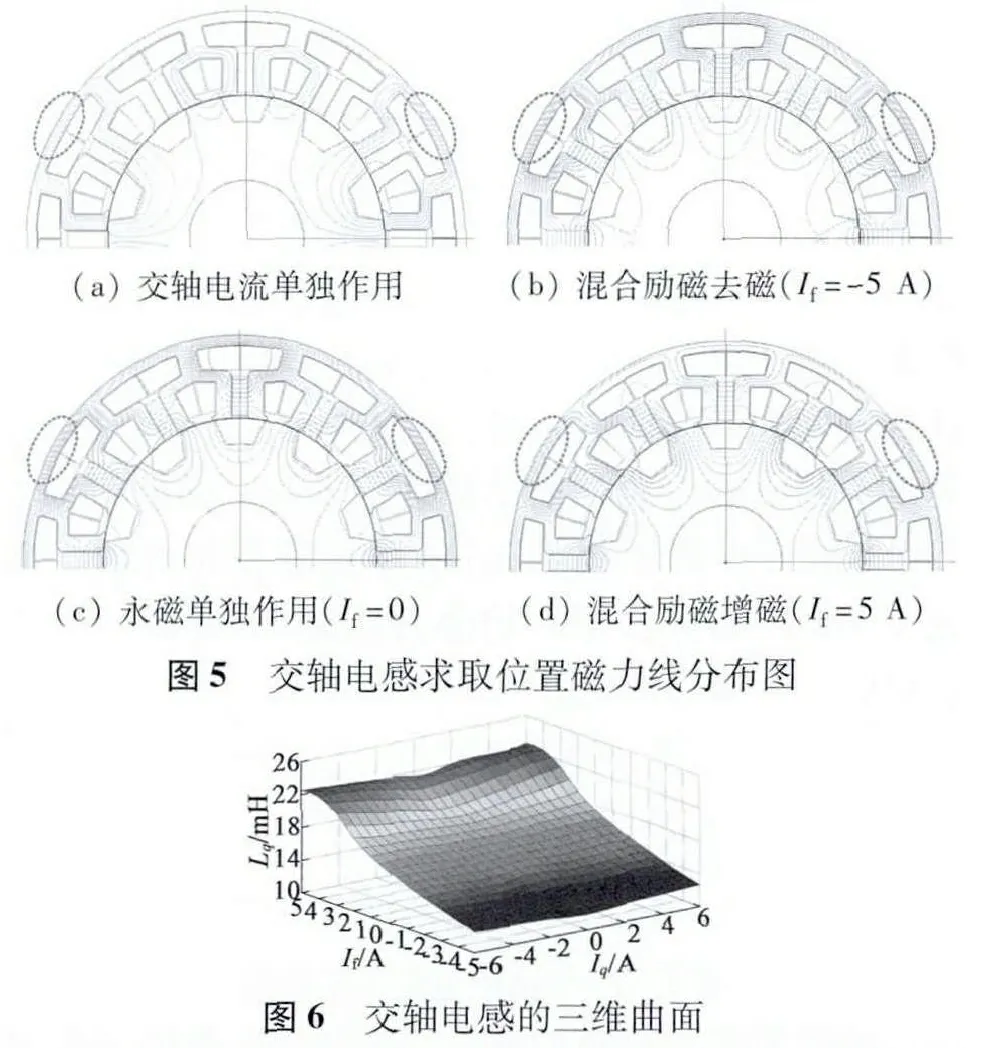
接着分析交轴电感Lq与励磁电流If变化的规律。随着电励磁电流的增加，经由定子磁桥段自闭合曲线的磁力线数量不断减少，而经由永磁体和气隙构成磁力线回路的数量则不断增加。由于硅钢片磁导率大于空气磁导率，因此磁桥段磁力线密度总体呈下降趋势，表现为Lq随If的增加而增加。

同理，分别改变If(－5 A≤If≤5 A)和Iq(－6 A≤Id≤6 A)，图6 给出了不同工况下交轴电感的三维非线性曲面。图6 中空间网格接近矩形分布所体现的Lq对Iq变化不敏感，以及三维曲面随励磁电流增加而单调上升的特性和磁力线分布图得到的分析结果一致。

3.4 交直轴电感拟合

为评估相同励磁电流作用下，交直轴电流变化对交直轴电感值的影响效果，定义波动范围:

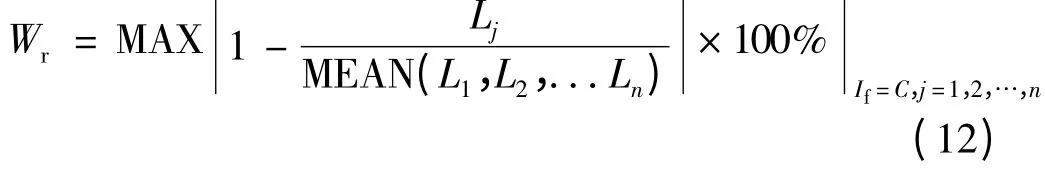
式中:MAX，MEAN 分别为最大值函数和平均值函数;n 为反映交直轴电流变化的样本数据量。

图7(a)给出了各励磁电流下的交轴电感波动范围，Lq的最大波动系数约为5.7%，因此，Lq可视作仅与If存在关联。进一步采用与Lev－If曲线相同的拟合方法，搜索发现选用四次多项式对不同励磁电流下的交轴电感平均值进行拟合，最大相对误差即可控制在3%以内。交轴电感曲面拟合表达式:

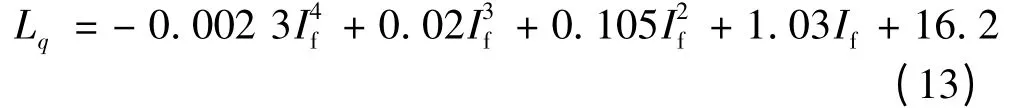
图7(b)显示Ld的最大波动系数高达62%，需要采用适当的曲面拟合技术生成便于计算机快速执行的曲面方程。基于最小二乘法拟合曲线方法改进并推广至三维空间拟合曲面的双三次多项式，具有较高的逼近精度［14－15］。在二维曲线拟合中，为避免高次多项式拟合过程中可能出现的龙格现象，已有不少学者尝试采用分段拟合方法［16－17］。本文通过分析电感波动范围确定合适的分段节点，并利用二维曲线与双三次多项式相结合的方法来实现直轴电感的三维非线性曲面的拟合。

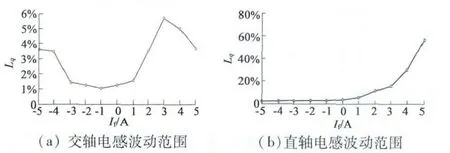
图7 交直轴电感波动范围

当If≤1 A 时，直轴电感Ld的最大波动系数约为5.1%，可忽略Id对Ld的影响，由此确定If=1 A为分段节点。与此对应的直轴电感曲面拟合表达式:

4 仿真与实验验证

4.1 交直轴电感仿真验证

图8 和图9 比较了三种工况下分别采用三相电感矩阵L(a，b，c)经坐标变换得到的交直轴电感，以及三维空间散乱数据点经曲面方程拟合得到的交直轴电感。对比结果显示，不论是永磁磁动势单独作用、混合励磁去磁，或是混合励磁增磁工作模式，两种方法得到的计算都比较接近，验证了曲面拟合方程具有较高的逼近精度，为电机建模创造了条件。

4.2 负载端电压仿真研究与实验验证

通过对FSHM 负载特性的仿真与研究，来验证三维电感曲线拟合方法的合理性以及电机模型的准确性。电流检测采用25 A 磁平衡霍尔电流传感器(匝数比5∶ 1 000)，采样电阻取为75 Ω，示波器探头选择×10 档，相当于将电枢电流放大至3.75 倍。在同一台计算机上运行二维有限元瞬态场求解器与Simulink 仿真模型，求解步长均设为20 μs，同计算一个电周期，前者约需30 min，后者仅需0.2 s。图10 给出了转速为1 200 r/min，星型连接电阻为60 Ω，三种励磁模式下的单相负载实测波形与仿真结果，对比结果显示相电压和相电流波形均近似正弦波，幅值和频率与仿真数据相一致，表明依据交直轴电感建立的转子坐标下的Simulink 模型可以较为准确地反映电机的输出特性，并且大幅度降低电机特性分析的计算成本。

图10 负载端电压实验与仿真波形比较

5 结 语

在建立三相静止坐标系下磁链和电压方程的基础上，采用磁链法计算了时变电感。分析了铁心磁桥饱和程度与电感参数的关系，指出磁桥式FSHM不能忽略电枢反应，相应由三相电感矩阵经坐标变换得到交直轴电感的方法存在较大难度。在对励磁电流和交直轴电流分别扫描的基础上，针对交直轴电感的非线性特点，依据电感曲线对电枢反应敏感性的差异，采用二维拟合与双三次多项式拟合相结合的方法构造了电感与多重激励电流的曲面方程，并据此搭建了Simulink 仿真模型。与有限元瞬态场仿真结果、实测波形对比显示，所建曲面方程描述的三维电感具有较高的逼近精度;基于该电感曲面方程建立的电机仿真模型可较好地反映磁桥式FSHM的实际工作特性，并具有运行速度快、准确度高的特点。

［1］ HOANG E，LECRIVAIN M，GABSI M.A new structure of a switching flux synchronous polyphased machine with hybrid excitation［C］//Power Electronics and Applications，2007 European Conference，Aalborg，Denmark，2007:1－8.

［2］ HUA W，CHENG M，ZHANG G. A novel hybrid excitation flux－switching motor for hybrid vehicles［J］. IEEE Trans. on Magnetics，2009，45(10):4728－4731.

［3］ JANG J S，LEE J K，KIM B T. Characteristic analysis of a hybrid excited flux switching PM motor by using the equivalent magnetic circuit method［J］. International Journal of Applied Electromagnetics and Mechanics，2012，39(1－4):843－849.

［4］ SULAIMAN E，KOSAKA T，MATSUI N.A novel hybrid excitation flux switching synchronous machine for a high－speed hybrid electric vehicle applications［C］//International Conference on Electrical Machines and Systems (ICEMS)，2011:1－6.

［5］ LIU X P，W C，ZHENG A H. Operation principle and topology structures of axial flux－switching hybrid excitation synchronous machine［C］//International Conference on Electrical Machines and Systems，2011:1－7.

［6］ HWANG C C，LI P L，LIU C T.Design and analysis of a novel hybrid excited linear flux switching permanent magnet motor［J］.IEEE Trans. on Magnetics，2011，48(11):2969－2972.

［7］ 花为，董广鹏，程明.混合励磁型磁通切换电机电感特性分析［J］.中国科技论文，2010，5(8):637－642.

［8］ 许泽刚，谢少军，许津铭.12/10 极混合励磁磁通切换电机的快速设计［J］.电机与控制学报，2013，17(3):76－83.

［9］ 张卓然，周竞捷，朱德明，等.多极低速电励磁双凸极风力发电机及整流特性［J］.中国电机工程学报，2009，29(6):67－72.

［10］ 张卓然，严仰光，周竞捷，等. 新型十二相梯形波永磁无刷直流发电机［J］.中国电机工程学报，2009，29(21):74－79.

［11］ HOANG E，AHMED A H B，LUCIDARME J.Switching flux permanent magnet polyphased synchronous machines［C］//7th European Conference on Power Electronic and Applications，1997，3:903－908.

［12］ 王莉.电励磁双凸极电机高压直流发电系统研究［D］. 南京:南京航空航天大学，2006.

［13］ HUA W，CHENG M，ZHANG G. Inductance characteristics of 3－phase flux－switching permanent magnet machine with doubly－salient structure［C］//5th International Power Electronics and Motion Control Conference，2006，3:1－5.

［14］ 张彩明，李雪梅，刘慧，等. 基于组合方法对图像的双三次多项式拟合［J］.中国科学，2011，41(9):1101－1111.

［15］ 尹士献，余学义，呼庆华.曲面拟合技术在开采沉陷预计中的应用［J］.西安科技大学学报，2010，30(5):518－522，530.

［16］ 张厚升，赵艳雷. 多项式拟合的光伏电池阵列模拟器研究与设计［J］.电力自动化设备，2012，32(2):109－113.

［17］ 李光辉，叶绪国. 基于Legendre 多项式的分段拟合［J］.统计与决策，2013，(18):28－31.