在线递推支持向量机的磁轴承转子位移预测

朱志莹，孙玉坤，李祖明，周云红，王正齐

(南京工程学院，南京211167)

0 引 言

主动磁轴承因其无摩擦、无磨损、超高速、长寿命、刚度可调、易于控制等一系列优点得到了广泛研究和应用［1－3］。位移检测环节是主动磁轴承系统重要组成部分。目前国内外实际实际磁轴承位移检测中多直接利用各类位移传感器，增加了系统复杂性，使得安装和调试不便，同时增加磁轴承转子轴向长度，降低临界转速，使得系统的优越性能发挥受限，因此探索无位移传感器的磁轴承转子位移自检测技术具有重要意义［4－6］。

由于磁轴承系统的本质非线性和参数不确定性，使得传统依赖于对象模型的转子位移自检测算法很难取得较好的检测效果。人工神经网络作为一种智能辨识方法能够摆脱对控制对象精确模型的依赖，在处理非线性和不确定性的问题中获得可处理性和鲁棒性［7］。但神经网络遵循经验风险最小化准则，存在训练样本规模过大、易陷于局部极小值等问题。为此，Vapnik［8］和Suykens［9］等人提出了一种新型机器学习算法——最小二乘支持向量机(以下简称LS－SVM)，该方法训练过程遵循结构风险最小化原则，不易发生过拟合现象，也不存在局部极小值问题，且小样本学习具有很强的泛化能力，近年来得到了广泛研究和快速发展。文献［10］将其用于磁轴承转子位移预测建模中，取得了比神经网络更好的应用效果。然而文献［10］将LS－SVM 用于位移预测建模时，基于离线学习算法，而实际磁轴承是一个时变不确定的系统，其电磁参数和运行工况随时间而变化，通过固定样本离线构建学习模型，并不能完全准确反映系统实际动态特征。

本文为实现主动磁轴承转子位移动态实时自检测，研究了一种在线递推LS－SVM 的磁轴承转子位移预测算法。首先对LS－SVM 进行改进，设定窗体宽度，使样本集随时间不断更新，并采用递推最小二乘法训练LS－SVM，实现LS－SVM 权值和阈值的在线递推式求解，提高计算速度;其次基于在线学习算法，建立磁轴承转子位移预测模型，该模型利用输入等效悬浮控制电流和等效磁链，实现转子位移的在线实时预测，仿真结果验证了算法的有效性。

1 在线递推最小二乘支持向量机

LS－SVM 算法是标准SVM 的一种改进，计算效率已经有了较大提升，但依然难以满足在线预测要求。这是因为在线学习样本是时间序列，不是批处理方式提供，每次引入新样本都需要从第一个样本开始重新学习，学习效率随着样本数目增多会急剧下降;同时引入在线学习后，LS－SVM 求解的线性方程组是时变的，需要不断地进行矩阵求逆运算，计算耗时较长。考虑到磁轴承系统的实际运行情况，在现有LS－SVM 基础上，进一步结合样本窗式更新和递推计算思想对其进行改进。设定在线学习样本窗的宽度固定为L，每进来一个最新样本，同时就丢掉一个最旧样本，使学习样本随时间t 不断更新而不是递增。这样既可以有效利用最新的样本集反映系统实时动态性能，又可以解决样本过大影响在线学习速度的问题。

假设t 时刻采样得到的输入输出样本集为{X(t)，Y(t)}，X(t)=［xt－L+1，…，xt－1，xt］，Y(t)=［Yt－L+1，…，Yt－1，Yt］，xt∈Rn为n 维输入向量，Yt∈R 为一维输出向量。在线LS－SVM 回归约束优化如下:

式中:k=0，1，…，L－1;φ(·)是从输入空间到特征空间的非线性映射;w 为权向量;bt为t 时刻偏置量;γ 为正则化参数;ek为松弛变量。

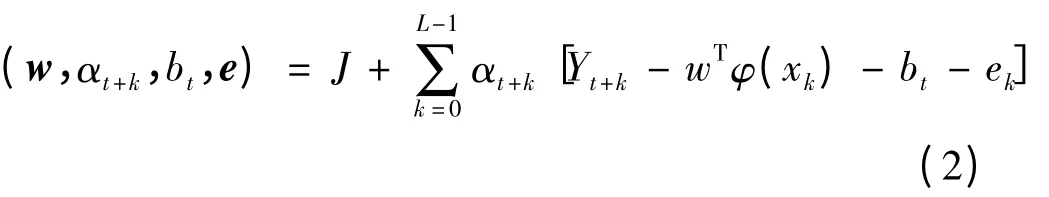
由式(1)定义拉格朗日函数如下:式中:αt+k为t 时刻拉格朗日乘子。由KKT［9］优化条件，对式(2)求偏导数，并消去ek和w，得到如下线性方程组:

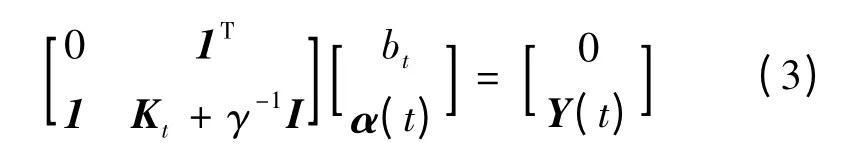
式中:1 =［1，…，1］T;I 为单位矩阵;α(t)=［αt－L+1，…，αt］T;Y(t)=［Yt+L－1，…，Yt］T;Kt为t 时刻核函数矩阵，元素Kt(i，j)=K(xt－i，xt－j)=φ(xt－i)Tφ(xt－j)，i，j=0，1，…，L－1。采用高斯径向基函数为核函数，表达式:

式中:σ 为核参数，反映边界封闭包含的半径。

设Pt=Kt+γ－1I，解式(3)线性方程组，可得:

这样在输入X(t)下的在线辨识模型:

由式(5)和式(6)可知，α(t)和bt求解涉及复杂的矩阵求逆运算，采用传统最小二乘法直接求逆运算量大，不利于在线学习，为此引入递推最小二乘算法。假设t 时刻有:θ=［bt，α(t)］T=［bt，αt－L+1，…，αt］T，Hk=［1，K(xt－L+1，xk)，…，K(xt，xk)］T，k=t－L+1，t－L+2，…，t。

设测试样本窗宽度亦为L，则采用递推最小二乘算法在线训练LS－SVM 步骤如下:

(1)初始化θ(0)=0，S(0)=δ－1I，δ 取小的正常数10－6，0 为零向量，I 为单位矩阵。

(2)取k =t－L +1，t－L +2，…，t。逐步刷新θ，即:

式中:Si为协方差矩阵;Mi为增益向量;θi为待辨识参数向量;λ 称为遗忘因子，其目的是减小旧数据的影响，增加新数据的作用，通常取0.95≤λ≤0.98，本文选取λ=0.98。

(3)若i≤t，返回步骤(2);否则，刷新完毕。

2 基于在线递推LS-SVM 转子位移预测

2.1 转子位移预测模型

LS－SVM 实现高度复杂的非线性映射，具有较快的运算速度，同时在线学习机制使得LS－SVM 具有自适应能力，能够随时间的变化而在线进化，可实现转子位移的在线预测。图1 给出了在线递推LS－SVM 建立磁轴承位移预测模型结构。输入为等效控制电流(ix，iy)和等效磁链(ψx，ψy)，输出为转子径向位移(x，y)，为简洁起见，此处图1 以位移x的预测为例作介绍。图1 中数据处理包含采样保持和窗式滚动两个步骤，其中采样保持的作用是通过对数据的采集、储存和延迟等操作;窗式滚动更新是数据缓冲区，将数据按时间顺序添加到时间窗内，转化为带时间特征的样本序列，并使样本集随时间不断滚动更新，以供模型在线学习使用。这样经过采样保持后得到的学习样本集，经过窗式滚动更新后，得到当前时刻最新的在线学习样本集，然后基于模型输出值与实际期望值之差，通过递推最小二乘算法(RLS)在线调整LS－SVM 模型参数，从而保证在t 时刻样本集的输入下，位移预测值与对象实际输出值匹配。

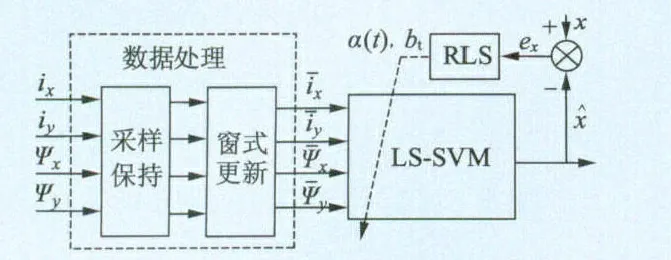
图1 基于在线递推LS－SVM 的转子位移预测模型结构

2.2 转子位移在线预测

运用在线递推LS－SVM 在线预测磁轴承转子位移主要包括以下几个步骤:

1)确定输入和输出变量。输入变量为磁轴承等效悬浮控制电流(ix，iy)和等效磁链(ψx，ψy)，输出变量为磁轴承转子径向两自由度位移x 和y。其中输入等效电流(ix，iy)可由三相交流电流iA，iB，iC经过C3/2变换得到:

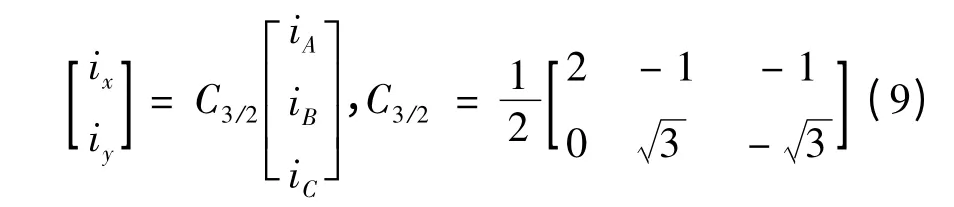
而三相电流可有电流传感器直接采集得到，而等效磁链无法直接检测得到，但可通过直接检测得到的电压、电流而间接得到磁链:

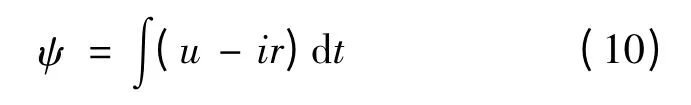
式中:u 为放大器的端电压;i 为绕组电流;r 为绕组等效电阻;ψ 为绕组磁链。

2)获取学习样本集。采集绕组电流、端电压和转子位移数据，通过C3/2变换和式(10)分别得到等效电流和等效磁链数据，并对实际数据进行采样保持和窗式滚动更新，将处理后时间长度为L 的电流、磁链和位移数据作为学习样本集。

3)选择RBF 型核函数的核宽度σ 以及处罚因子γ。为了提高LS－SVM 的预测能力，避免人为选择参数的盲目性，本文利用粒子群优化算法［10］对参数(σ，γ)进行自动寻优。

4)利用递推最小二乘法训练两个LS－SVM 模型，获得相应参数θ1= (，α1(t))和θ2= (，α2(t))，从而根据当前的输入X(t)，预测模型在线预测出转子的位移x 和y。

随着我国经济以及社会的快速发展，我国迅速进入数字化时代，此时信息发现、信息分析整合、信息管理以及信息创新应用都发生了很大的改变。在此背景下，如何加强我国党校图书馆的信息整合建设，受到了我国党和政府的高度重视。习近平总书记曾指出：我国的党校图书馆信息整合建设应重点从提高信息质量、推动信息创新方面下手。加强党校图书馆为党政部门决策所提供的的信息资源和服务，实现我国党政建设的健康发展。

5)利用测试样本集检验预测精度是否达到目标要求，符合要求，则预测结果有效，转步骤6);否则转步骤4)。评价模型采用均方根误差:

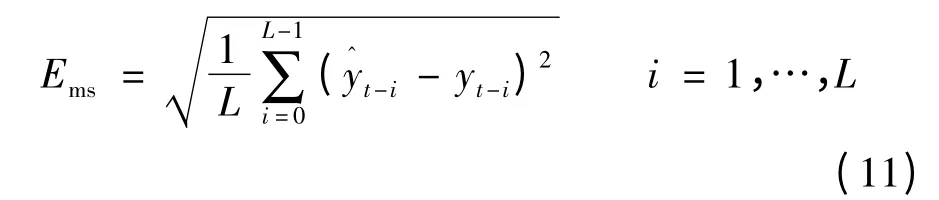
6)采集t+1 时刻电流和位移数据，剔除t－L+1 时刻的数据，采集t+1 时刻的期望位移，并将计算结果加入期望数据集，令t= t+1，转至步骤4)。

2.3 基于在线递推LS－SVM 的转子位移预测控制

以一台三相交流主动磁轴承为例，介绍在线递推LS－SVM 转子位移预测控制算法。图2 给出了三相交流主动磁轴承结构示意图。由图2 可见，三个U 型电磁铁沿圆周120°均匀分布，I0为偏置绕组中的直流电流，提供静态偏置磁通;iA，iB，iC为三相交流电流［4］。

图2 三相交流主动磁轴承结构示意图

忽略3 个磁极间的磁路耦合、漏磁、铁心磁阻、转子磁阻及涡流损耗等，根据磁路等效法，可得磁轴承悬浮力计算公式:

式中:I0为偏置绕组直流电流;S 为磁极截面积;δ0为磁极下气隙长度;μ0为空气的磁导率。

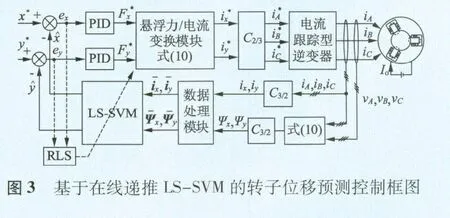
根据三相交流主动磁轴承的悬浮力模型，结合在线梯度LS－SVM 位移预测原理，构建如图3 所示的磁轴承转子位移预测控制框图。图3 中，三相绕组电流和电压由传感器直接检测得到，等效电流和等效磁链(ix，iy，ψx，ψy)经过C3/2和式(10)得到，通过数据处理模块形成在线窗式学习数据，LS－SVM模块根据输入样本集，得到转子位移预测值和，与参考值x*和y*进行比较，经PID 调节器和力/电流转换模块得到两相等效电流指令，经过C2/3变换得到三相电流的指令值，，再经过逆变器控制产生三相电流实际值iA，iB，iC，控制磁轴承转子悬浮。

3 仿真分析研究

根据本文提出的转子位移预测方法，在图2 控制框图基础上进行仿真验证。仿真所用磁轴承样机参数如表1 所示，转子初始位移为x=y =－0.2 mm。

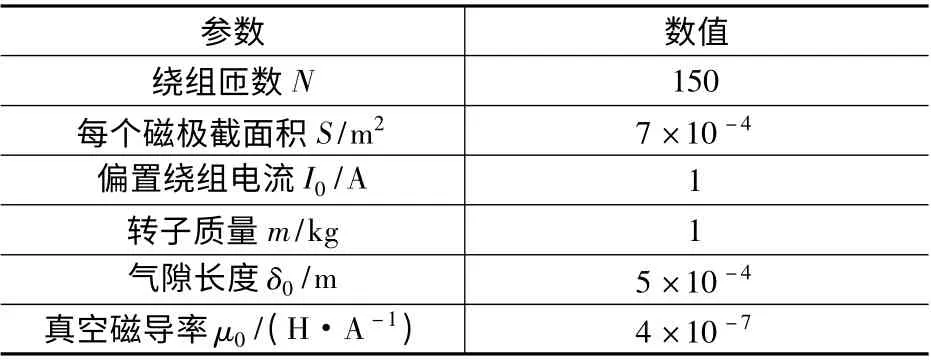
表1 磁轴承模型参数

图4 是空载起浮时转子在径向位移x 和y 的实际值和预测值对比曲线。从图4(a)的转子径向位移曲线可以看出，基于在线递推LS－SVM 的转子预测位移能够准确、快速地跟踪转子实际位移，并最终稳定悬浮在平衡位置处。从图4(b)的位移误差曲线可以进一步看出，预测误差分布具有如下特点:①转子稳定悬浮阶段预测误差小于起浮阶段的预测误差，主要是因为:转子在稳定悬浮阶段基本无径向位移，而在起浮阶段径向位移波动较大，使得在线算法的回归计算时间较长，从而导致了预测位移滞后于实际位移;②对于同一预测位移，在较为平滑的上升或下降段预测精度较高，而在曲线拐点处的预测误差较大，这主要是由于在拐点处曲线趋势发生变化，导致算法的预测精度有所下降。③位移最大预测误差为28 μm，远小于气隙长度0.5 mm。因此所述在线递推LS－SVM 具备较高的预测精度。

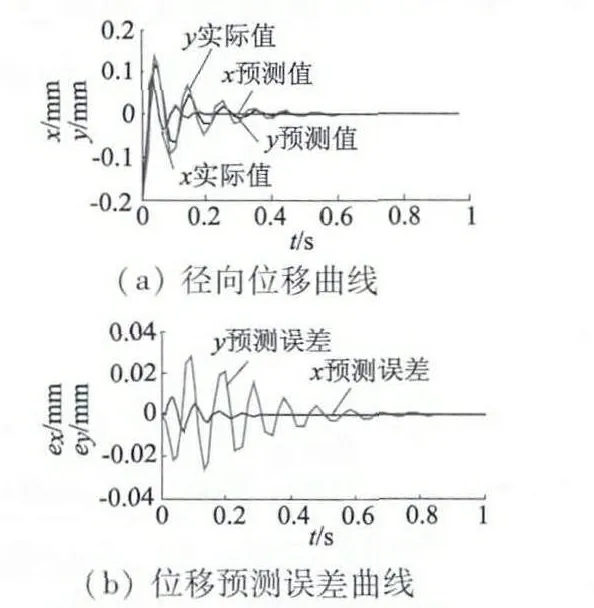
图4 位移实际值与预测值

为进一步验证在线递推LS－SVM 位移预测算法的优越性，将其与传统离线LS－SVM 位移预测算法进行对比研究。对比研究中，在转子稳定悬浮时对径向两自由度施加冲击负载，观察两种算法下转子位移响应情况。图5 和图6 分别给出了x 方向冲击负载和y 方向冲击负载作用下两种算法的位移响应波形。

图6 y 方向冲击负载仿真波形

从图5 和图6 可以看出，对两个自由度施加冲击负载后，在两种预测算法控制下，磁轴承转子在经过一个单边抖动后都能回到平衡位置，这表明了离线LS－SVM 和在线递推LS－SVM 的位移预测控制均能实现转子稳定悬浮运行。这体现了LS－SVM预测控制算法的有效性。同时，进一步比较图5(a)、图5(b)以及比较图6(a)、图6(b)可以看出，当冲击负载消失以后，在线递推LS－SVM 算法作用下转子径向波动幅值明显小于离线LS－SVM 算法下的转子波动幅值，这说明在线递推LS－SVM 预测算法采用在线学习后，使其对对象变化具备更强的适应能力，因而所提在线递推LS－SVM 预测算法具有更强的适应性。

4 结 语

本文采用在线递推LS－SVM 进行磁轴承转子位移在线预测研究，理论分析与仿真结果表明:

1)利用样本窗式更新和递推最小二乘法实现在线递推LS－SVM 算法，提高了计算速度，使其满足在线学习的要求;

2)基于在线递推LS－SVM 预测模型能够较好地映射出等效电流、磁链与转子位移的实际动态关系，具备较高的预测精度和自适应能力;

3)在线递推LS－SVM 的磁轴承转子位移预测控制方案，避免了位移传感器的不利影响，简化了悬浮控制系统的结构，提高了系统的可靠性。

［1］ SCHWEITZER G，BLEULER H，TRAXLER A. Active magnetic bearings［J］.vdf Hochschulverlag AG，ETH Zurich，1994.

［2］ 周丹，祝长生，王玎. 电磁轴承用磁通控制型功率放大器力增益的研究［J］.电工技术学报，2012，27(1):188－195.

［3］ 楼晓春，吴国庆.主动磁轴承系统的自适应滑模控制［J］.电工技术学报，2012，27(1):142－147.

［4］ 黄振跃，邹海丹，朱熀秋，等.三相交流主动磁轴承位移自检测技术仿真研究［J］. 中国电机工程学报，2009，29(S1):228－233.

［5］ 金婕，朱熀秋.磁悬浮轴承转子位移自检测方法［J］.微电机，2014，47(9):79－84.

［6］ 于洁，祝长生.基于希尔伯特变换的自传感电磁轴承实现［J］.浙江大学学报:工学版，2015，49(4):732－739.

［7］ 王喜莲，葛宝明，伍召莉.基于柔性神经网络自适应PID 的磁轴承径向力控制［J］. 北京交通大学学报，2012，36(2):85－90.

［8］ VAPNIK V. The nature of statistical learning theory［M］. New York:Springer－Verlag，1999.

［9］ SUYKENS J A K，VAN GESTEL T，DE BRABANTER J，et al.Least squares support vector machines［M］.World Scientific Publishing，2002.

［10］ 朱志莹，孙玉坤.群优化支持向量机的磁轴承转子位移预测建模［J］.中国电机工程学报，2012，32(33):118－123.