基于MPSO-BP 的超声波电动机Hammerstein 模型建模

邢 航，张铁民，张建桃，杨秀丽，漆海霞

(华南农业大学，广州510642)

0 引 言

超声波电动机是通过压电元件产生超声波振动来驱动的新型电机，它具有很多优点，如起动转矩大、结构简单、不受电磁干扰、不产生电磁干扰等，但它随着驱动条件不同具有严重非线性以及负载依赖性，因此，超声波电动机建模是一件困难并有挑战性的工作，其建模的理论和方法有很多，如等效电路建模、有限元建模、解析法建模等，但这些方法都较复杂，难以实用。从实现超声波电动机高精度控制的角度，系统辨识法可以克服上述方法在控制器设计中存在的问题［1］。

文献［2］提出了一种基于Hammerstein 结构的超声波电动机建模方法，但该方法不仅复杂而且由于采用试凑法提取参数，不适合所有超声波电动机，因为即使是同类型的超声波电动机，除了动态特性不同外，静态特性也是不同的，且该方法处理时间长。文献［1］提出一种超声波电动机Hammerstein模型建模方法，该方法需要识别死区，但考虑了驱动电压对模型参数的影响。文献［3］提出的Hammerstein 模型，其非线性静态部分采用RBFNN 结合遗传算法来近似，线性动态部分采用一阶传递函数。

粒子群优化算法(以下简称PSO)与遗传算法很相似，都是基于迭代的优化算法，都具有全局、并行搜索特性，都可以用于识别非线性系统模型的参数。但与遗传算法相比，PSO 算法的优点是实现简单，性能良好，因此在短短几年间得到了快速发展。本文提出一种超声波电动机的Hammerstein 模型的建立方法，其非线性静态部分采用改进的粒子群优化BP(以下简称MPSO－BP)算法来近似，线性动态部分采用一阶传递函数模型。

1 超声波电动机建模

1.1 Hammerstein 模型

Hammerstein 模型由非线性静态模块和线性动态模块串联而成，结构如图1 所示。

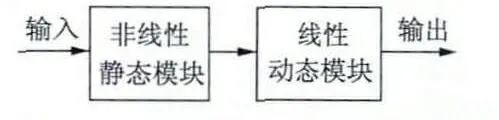
图1 Hammerstein 模型结构

在本文中，超声波电动机两相电压的相位差Φ 是输入的控制变量，v 是非线性部分的输出，是一个中间变量，ω 是Hammerstein 模型的输出。Hammerstein 模型的非线性静态部分采用MPSO－BP 算法建模，线性部分采用一阶传递函数模型，如图2 所示。

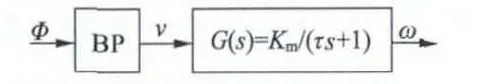
图2 超声波电动机的模型结构

一阶传递函数［4］:

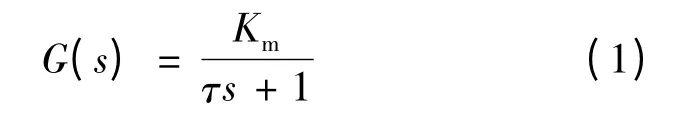
式中:Km是超声波电动机的静态增益;τ 是时间常数;模型的参数可以从测量数据中提取。USR60 超声波电动机的参数如下［4］:Km=10.25，τ =0.003 5 s。

Hammerstein 模型的非线性静态部分采用如图3 所示的BP 神经网络来建模。输入层一个节点，为Φ，输出层一个节点，为ω。设隐层节点n 个，ω1i(i=1，2，…，n)是输入层和隐层节点间的连接权值，vi1(i=1，2，…，n)是隐层与输出层节点间的连接权值。隐层输出函数如下:

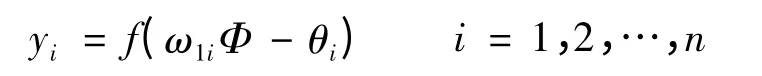
输出层单元的输出函数如下:

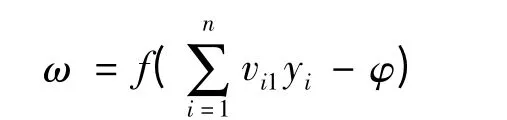
式中:yi(i=1，2，…，n)为隐层输出;θi是隐层阈值;φ 是输出层阈值，f(·)为神经元激活函数。

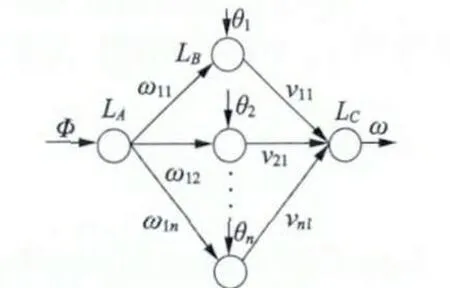
图3 BP 神经网络结构

由于BP 算法的优劣主要取决于初始权值和阈值选择，如果选择不合适，容易陷入局部最小，因此，本文利用MPSO 算法的全局搜索能力以及BP 算法的局部搜索能力，来优化初始权值和阈值，使其避免陷入局部最小。

1.2 MPSO－BP 算法

PSO 算法是1995 年提出的一种迭代进化算法，该方法从随机解出发，通过不断地寻找当前空间中的最优值来搜寻全局最优解。

1)标准PSO 算法

标准PSO 算法假设N 维空间中有m 个粒子，第i 个粒子在N 维空间中的位置用xi=(xi1，xi2，…，xiN)来描述，粒子的飞行速度vi=(vi1，vi2，…，viN)，适应度值由目标函数确定，每个粒子当前位置为xi，截止当前最好的位置为pbest，在整个群体中最好的位置为gbest(gbest是pbest的最优值)［5］，并用下面的公式来更新第i 个粒子的速度和位置，即通过第k 级推导第k+1 级的数据:

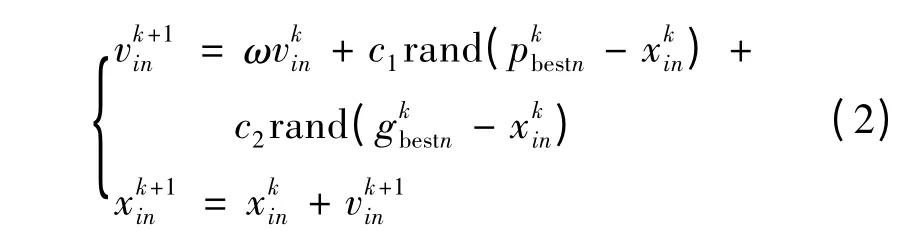
式中:c1，c2为加速度因子，用于调节每个迭代步的大小;rand()为［0，1］之间的随机数，i =1，2，…，N;k 为迭代个数;ω 为惯性因子。

2)改进的粒子群优化算法

在PSO 算法中，惯性因子较大，有利于跳出局部最小，实现全局搜索;惯性因子较小，便于实现局部搜索，算法易收敛。为了在全局和局部搜索之间找到最好的惯性因子，本文采用改进的惯性因子来改变收敛速度和精度。为了解决局部粒子早熟线性，并避免后面所有粒子集中于一个极值点附近，采用自适应速度调节因子，改进后的粒子群算法如下:

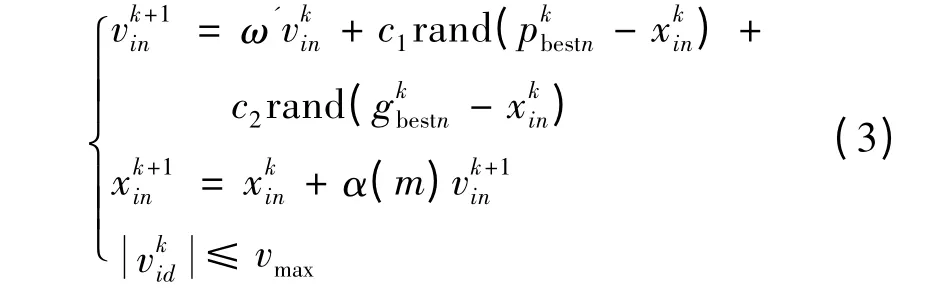
式中:α(m)是速度调节因子，m=1，2，…，j，j 是速度区间系数;ω'为改进的惯性因子。

惯性因子的改进策略如下:

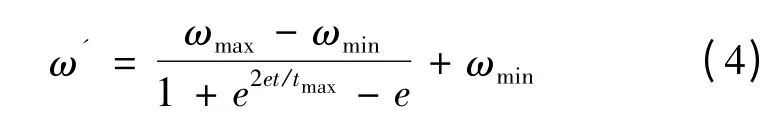
式中:ωmax和ωmin分别是惯性因子的极大、极小值;t和tmax分别为当前的迭代个数和最大迭代个数;e 是用来调节速度变化的控制因子，一般e =10。这种方法可以实现在寻优的早期粒子保持高速飞行，在寻优中期逐渐将飞行速度减速，在寻优的后期保持一定的飞行速度以进行最后的收敛［6］。

速度调节因子α(m)用于决定放大或缩小粒子的新位置，函数如下［7］:

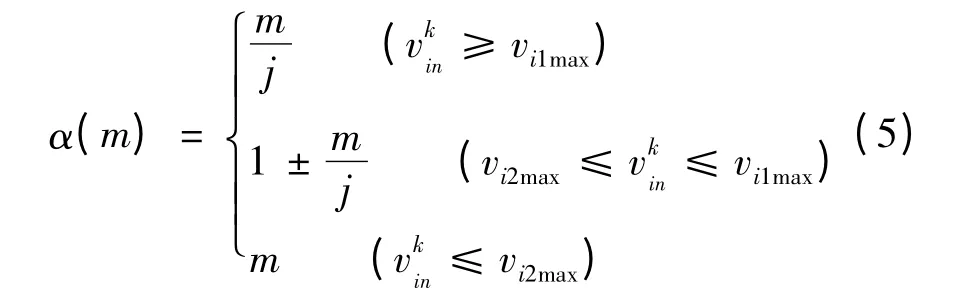
假设最大速度为vi1max，最小速度为vi2max，当≥vi1max时，α(m)减小寻优速度;当≤vi2max时，α(m)增大寻优速度;当vi2max≤≤vi1max时，将两个方向的大小放大或缩小，于是粒子可以有足够求解空间。

3)基于MPSO 算法的BP 神经网络算法

假设MPSO 中位置向量X 的元素是神经网络各个节点之间的权值和阈值，p 为样本数，c 为输出节点数为神经网络的期望输出，xi，j是神经网络的实际输出。每次迭代都找到一个最优的权值和阈值使得下面的均方误差最小:

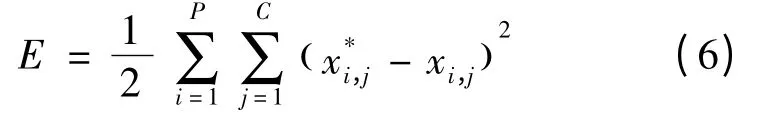
基于MPSO 算法的BP 神经网络优化过程如下:1)建立BP 网络拓扑结构。2)初始化粒子群。初始化粒子的随机位置和速度，初始化迭代次数的最大值，将当前位置作为粒子的初始最好位置。3)将粒子的初始位置作为初始权值和阈值赋予BP 网络。4)确定个体的极值点。训练网络，计算粒子的适应度值(用式(6))，如果粒子的当前适应度值比历史上最佳适应度值更好，则将粒子当前位置赋予历史最好位置。5)确定全局最优极值。将每个粒子的当前阈值与gbest进行比较，如果当前适应度值比gbest小，则将当前适应度值赋给gbest。6)根据式(3)、式(4)、式(5)来更新粒子的速度和位置。7)当迭代次数达到最大值或最小误差限时，停止迭代，全局极值就是训练过程的最优解，它就是神经网络权值和阈值，否则转到步骤4)执行。

采用上述训练结果，结合一阶线性模型来完成超声波电动机Hammerstein 模型的建模和测试。

2 仿真与测试

2.1 测试数据和参数设置

超声波电动机控制变量主要为两相输入电压频率、幅值和相位。本文的研究对象为USM60 超声波电动机，负载TL=0，本文主要讨论当输入为相位差时的Hammerstein 速度模型。超声波电动机的动态线性部分采用一阶传递函数描述，非线性静态部分采用MPSO－BP 算法来逼近，在BP 神经网络中输入层为一个神经元φ，隐层为3 个神经元，传递函数为logsig，输出层一个神经元ω，传递函数为purelin，神经网络误差限为10－4，迭代次数为1000，超声波电动机输入相位在［－90°，90°］之间每隔10°输入，分别在输入电压频率为41.5 kHz，42 kHz，42.5 kHz情况下输入相位差信号，获得三组数据，将这三组数据作为网络训练样本集。本文中，采用MPSO－BP神经网络建模方法建立Hammerstein 模型静态非线性部分，MPSO 算法的参数设置如下:ωmin=0.1，ωmax=0.9，c1=2，c2=2，r1，r2是［0，1］之间的随机数，粒子群数量为100，粒子速度范围在(0，0.5)之间。

2.2 预测结果和误差分析

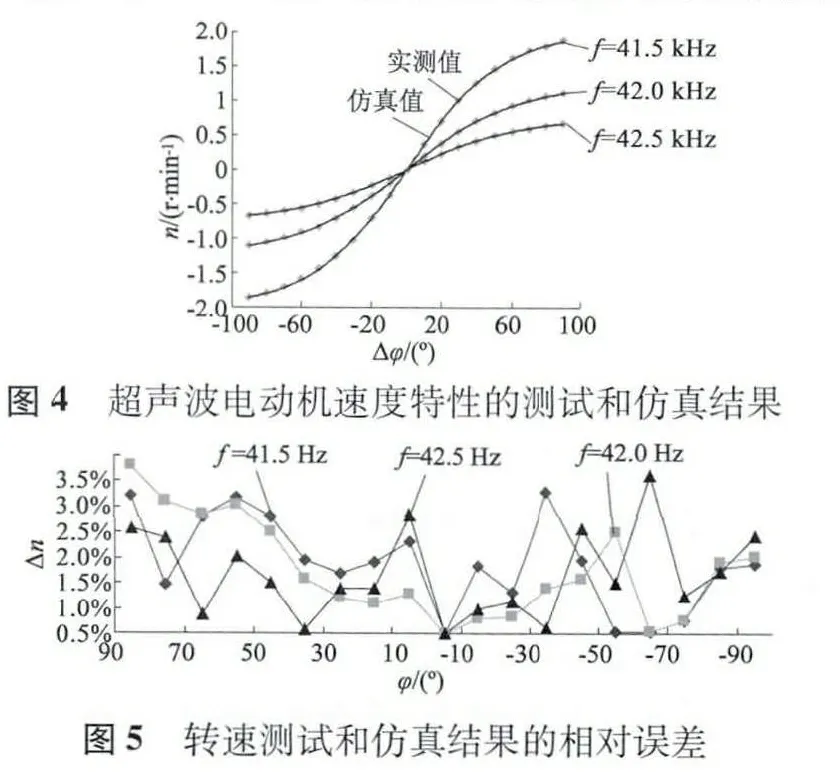
下面给出仿真结果以说明本文给出的方法的意义。驱动电压峰峰值为360 V，驱动频率分别为41.5 kHz，42 kHz 和42.5 kHz，系统输入信号为相位差，输出为速度，测试数据和仿真数据的比较如图4 所示，误差分析如图5 所示。三种情况下，系统的均方误差分别为1.38，0.9，0.45，最大相对误差为2.79%，3.3%，3.14%。可以看出，采用MPSO－BP 神经网络的Hammerstein 模型预测精度更高一些，采用此方法建立的超声波电动机模型可行且实用。

3 结 语

本文采用MPSO－BP 算法建立超声波电动机Hammerstein 模型，其中非线性静态部分采用MPSOBP 神经网络建模，线性动态部分采用一阶传递函数模型。仿真和实验分析结果显示，该方法建立的模型和实验数据较吻合，准确度较高，是复杂非线性系统的一种可行的建模方法，为高性能控制器的设计提供了基础研究。

［1］ ZHANG Xin－liang，TAN Yong－hong.Modelling of ultrasonic motor with dead－zone based on Hammerstein model structure［J］. Journal of Zhejiang University:SCIENCE A. 2008，9(1):58－64.

［2］ BIGDELI N，HAERI M.Modeling of an ultrasonic motor based on hammerstein model structure［C］//Control，Automation，Robotics and Vision Conference，2004，2(8):1374－1378.

［3］ JAHANI M，MOJALLALI H. Neural network based modeling of traveling wave ultrasonic motor using genetic algorithm［C］//International Conference on Computer and Automation Engineering(ICCAE)，2010，(5):486－490.

［4］ SENJYU T，YOKODA S，GUSHIKEN Y，et al. Position control of ultrasonic motors with adaptive dead－zone compensation［C］//Institute of Electric and Electronic Engineer Industry Applications Conference，33rd IAS Annual Meeting，1998，(1):506－512.

［5］ 郭亮，陈维荣，贾俊波，等.基于粒子群算法的BP 神经网络光伏电池建模［J］.电工电能新技术，2011，30(2):84－88.

［6］ 王建国，阳建宏，云海滨，等.改进粒子群优化神经网络及其在产品质量建模中的应用［J］. 北京科技大学学报，2008，30(10):1188－1193.

［7］ 师彪，李郁侠，于新花，等.改进粒子群－BP 神经网络模型的短期电力负荷预测［J］.计算机应用，2009，29(4):1036－1039.