轮迹位置对钢桥面板U 肋对接焊缝疲劳性能的影响

朱 伟，吉伯海，傅中秋

(河海大学 土木与交通学院，江苏 南京210098)

0 引 言

疲劳［1］是结构在反复荷载作用下产生的裂纹的生成、不断扩展、最终导致构件断裂的现象。正交异性钢桥面板因其自重轻、承载力大、施工速度快等优点，而广泛应用于大中跨径的钢桥中。日常频繁的车流荷载作用下，纵肋受到扭转和弯曲综合作用，容易处于拉压循环的应力状态，再加上U 肋对接焊缝部位现场施工对中存在偏差或者焊接质量不能得到保证，使得在纵肋对接焊缝处易产生疲劳损伤。此外，据日本钢结构委员会对日本阪神高速公路和首都高速公路钢桥面板的钢桥疲劳裂纹统计结果，纵肋对接焊缝是四大易疲劳部位之一［2-3］。

由于正交异性钢桥面板构造复杂，各疲劳细节的应力幅值对车轮作用位置较为敏感，车辆在桥面不同横向位置行驶时，各构造细节的应力循环特征不同，导致应力峰值出现的概率也有较大的差异，并最终影响各疲劳细节的应力谱。因此，轮迹位置是影响正交异性钢桥面板疲劳性能的重要因素。针对轮迹位置对疲劳的影响，国外已进行大量的研究，如欧洲规范［4-5］和荷兰规范NEN6788 等［6］均已明确给出了车辆轮迹线横向位置概率分布模型，并以应力幅折减系数的形式体现到设计规范当中。然而我国在这方面的研究较少，设计规范中尚未对轮载的横向分布概率作具体规定。本文中以江阴长江大桥为研究对象，通过数值模拟的方法，分别研究车辆轮迹位置对U 肋对接焊缝开裂前以及开裂后的疲劳性能影响。

1 有限元分析模型

采用ANSYS 有限元软件建立江阴长江大桥局部有限元模型，分析车轮横向位置对正交异性钢桥面板典型构造细节疲劳应力幅的影响，有限元模型如图1 所示。顺桥向取4 个横隔板间距，横桥向取7 个U 肋的宽度。桥面板厚度为12 mm，U 腹板尺寸为300 mm×6 mm×280 mm，U 肋之间间距为300 mm，横隔板间距为3.2 m，采用shell63 单元模拟;荷载取英国规范［7］中标准疲劳车中的一个轮载，加载工况及测点如图2 所示，图中e 为车辆轮迹中心线偏移待测U 肋中心的横向距离，每移动150 mm 作为一个加载工况，共计算7 个工况，以分析车辆轮迹位置对开裂前的U 肋对接焊缝疲劳影响分析。

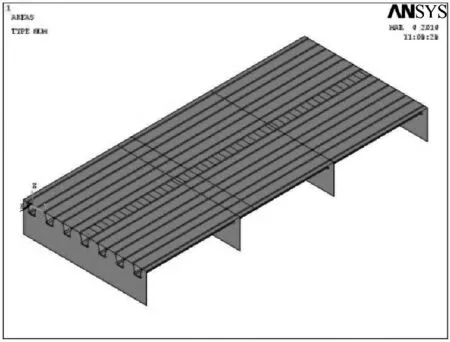
图1 模型示意图Fig.1 The finite element model

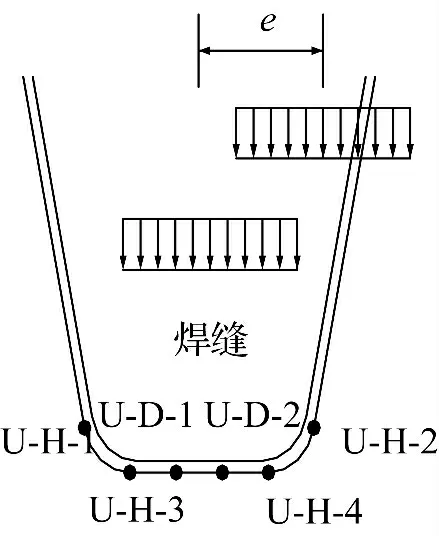
图2 加载工况及测点示意图Fig.2 The loading position and measuring point

针对开裂后的裂纹扩展分析，分别利用ANSYS 以及FRANC2D/L 建立U 肋对接焊缝的局部模型，进行了相同荷载作用下(-100 MPa)的两种模型计算，并提取两模型垂直焊缝方向、沿焊缝方向的应力变化情况，以对比验证FRANC2D 计算结果的准确性，计算结果如图3 所示。

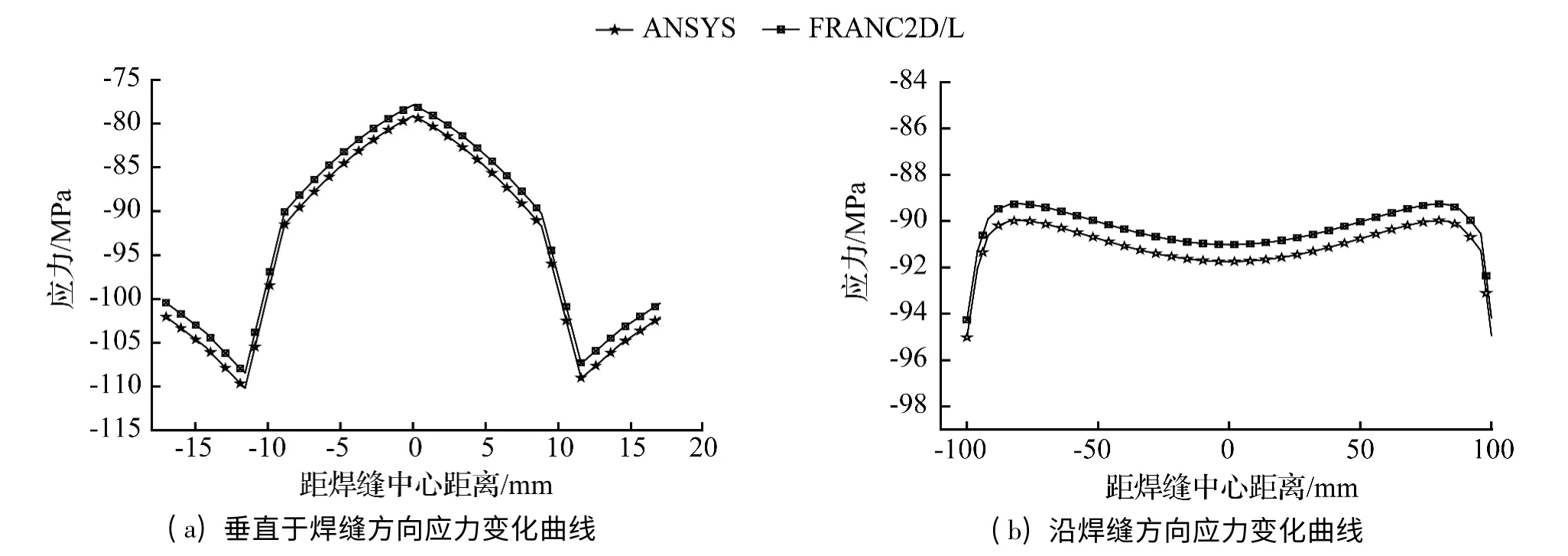
图3 焊缝处应力分布Fig.3 The stress distribution of butt weld

沿焊缝方向的变化规律如图3(b)所示，均匀拉力作用下，距离焊趾越近，其周围应力越大，并在焊趾处达到最大值，焊缝余高中心处应力最小;垂直于焊缝方向的变化规律如图3(a)所示，均匀拉力作用下，焊缝两端边缘应力最大，距离焊缝中心越近，焊趾处应力先减小后增大，并在焊缝中心处达到最大。应力云图如图4 所示。

经对比，两种模型所计算得到的应力变化规律一致，且两种模型所得到的相同位置处的应力大小相差较小，最大仅为0.9%。因此，FRANC2D/L 可以较为准确的模拟。

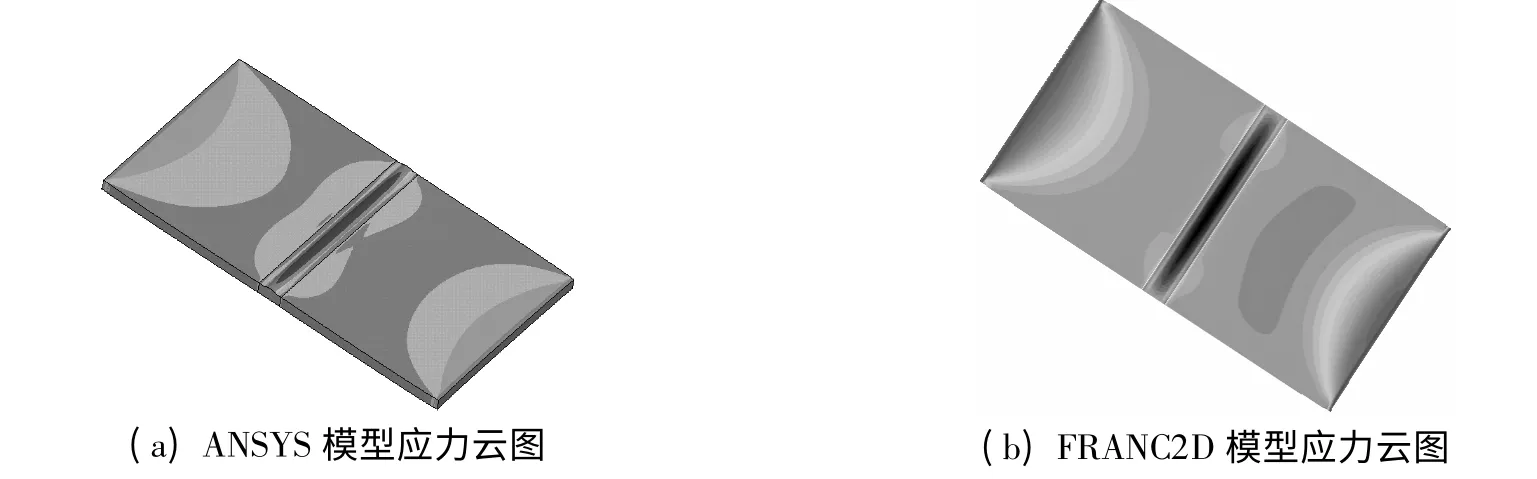
图4 焊缝局部应力云图Fig.4 The local stress nephogram of butt weld

现利用FRANC2D/L 分别建立焊缝与母材的局部模型，分别建立焊缝与母材的有限元模型，并采用层状分析技术将焊缝黏贴于母材上，以模拟U 肋对接焊缝。同时在焊缝中央边缘焊趾处设置一长度为4 mm 的初始裂纹，如图5 所示，以分析车辆轮迹位置对开裂后的U 肋对接焊缝疲劳性能影响分析。

图5 裂纹扩展模型以及初始裂纹示意图Fig.5 Crack propagation model and initial crack

2 轮迹位置对疲劳应力的影响

2.1 应力幅分析

根据课题组前期对江阴长江大桥应力监测结果，发现实桥U 肋嵌补段底部应力较大，容易产生疲劳裂纹，选取U 肋对接焊缝底部6 个部位进行应力的提取，以分析不同车轮位置对U 肋对接焊缝的疲劳应力幅以及U 肋对接焊缝不同位置的损伤分布情况，计算结果如图6 所示。

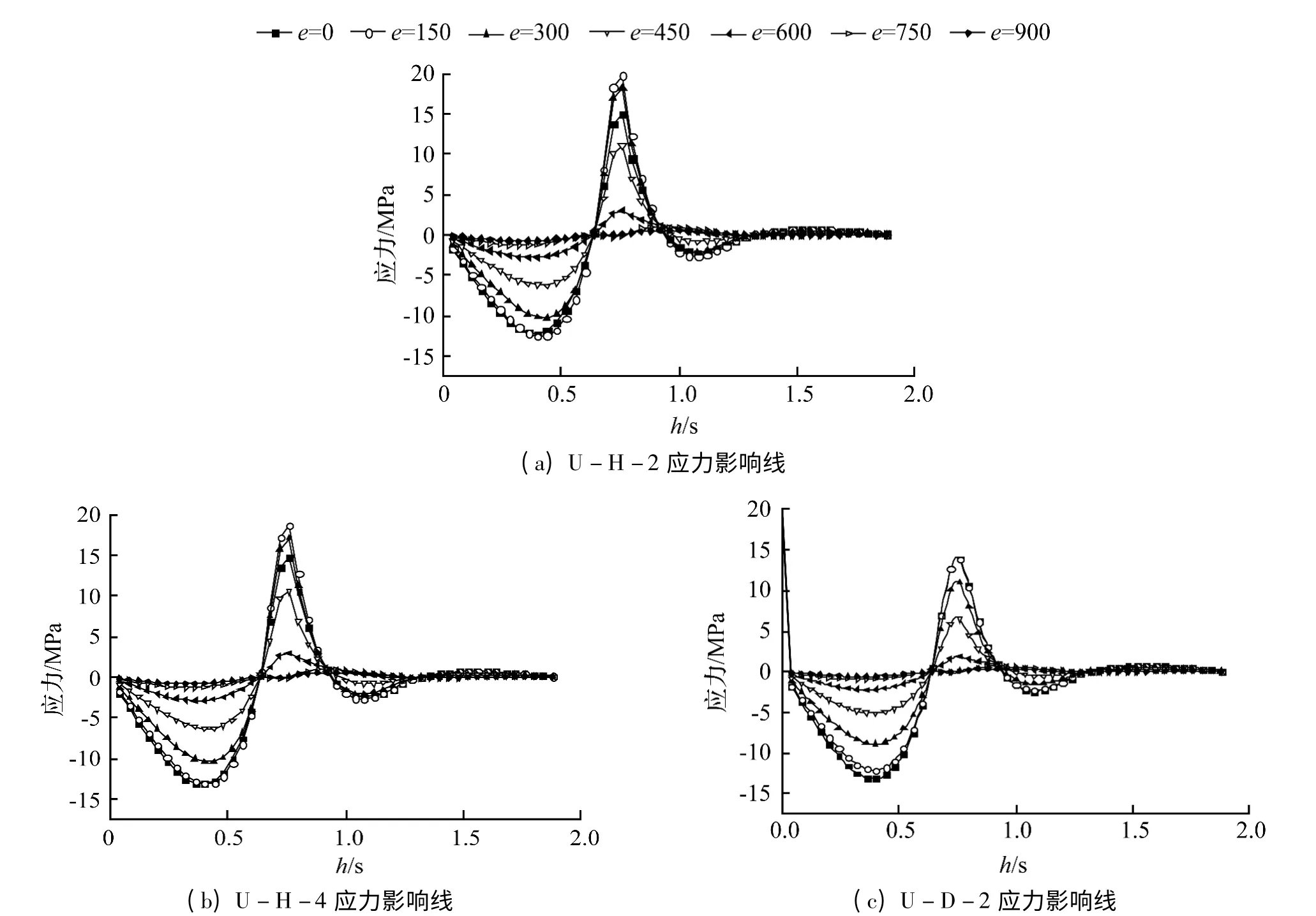
图6 各测点应力影响线Fig.6 The Stress curve of measuring points

由图6 可知，各测点的应力变化曲线可以得出，车轮经过测点U-H-2、U-H-4 以及U-D-2 正上方时，各测点应力迅速增加，车轮偏离测点时各测点拉应力迅速下降，且随着车轮的移动，U 肋对接焊缝处呈现，先“压”后“拉”再“压”再“拉”的应力变化趋势。如图6(a)所示，当e=0 时产生的最大拉应力为14.9 MPa(最大应力)，e=150 mm 时产生的最大拉应力为5.95 MPa，e 为＞300 mm 时最大拉应力已低于1 MPa，因此U 肋对接焊缝处各部位应力对车轮位置较为敏感。

应力幅是决定构件疲劳性能的关键因素之一［8-9］，因此有必要分析车轮位置对应力幅的影响。如图6(a)所示，经计算，e=0(最不利位置)时产生的最大疲劳应力幅为27.1 MPa;e=150 mm 时最大应力幅为15.2 MPa，相对于最不利位置降低了43.9%;e=300 mm 时产生的最大应力幅为6.3 MPa，相对于最不利位置降低了76.8%;e=450 mm 时产生的最大应力幅为2.7 MPa，相对于最不利位置降低了90%;当e ＞600 mm 时最大应力幅已低于1 MPa，对U 肋对接焊缝处的疲劳损伤几乎可以忽略不计。因此，车辆轮迹位置对U 肋对接焊缝处的疲劳应力幅影响距离较小，根据本文计算结果该细节的横向疲劳影响范围为600 mm。由此，当车辆之间的横向距离大于600 mm 时，可不必考虑多车效应。

2.2 疲劳损伤分析

为了更加直观的分析横向车轮位置对正交异性钢桥面板U 肋对接焊缝处疲劳损伤的影响，以及同一U 肋对接焊缝不同部位的损伤情况。现根据BS5400 规范，确定构造细节的疲劳抗力等级，选择可接受的失效概率，得到U 肋对接焊缝构造细节的S-N 曲线，按照Miner 法则计算其疲劳损伤度。计算结果如表1所示。由于当e ＞600 时车轮位置对疲劳损伤的影响较小，可以忽略，因此现仅分析e≤600 的各工况。

表1 各测点疲劳损伤度Tab.1 The fatigue damage degree

由表1 可知，随着车轮位置的改变，即e 的增加，损伤度依次降低，与应力幅变化规律一致。现对比不同车轮位置作用下U-H-2、U-H-4、U-D-2 三个测点的疲劳损伤度，不难发现，U-D-2 的疲劳损伤度明显低于U-H-2、U-H-4，最低仅为U-H-2、U-H-4 的9.7%，变化趋势如图7 所示。

由图7 可知，随着车轮位置的改变，e 的增加，疲劳损伤差异程度先急剧增大后趋于减小并最终达到稳定。当e=300 mm 时，疲劳损伤差异达到最大，当e ＞300 mm 时，疲劳损伤差异趋于减小，当e=450 mm 时趋于稳定。

综上所述，车辆轮迹位置对U 肋对接焊缝开裂前的疲劳性能影响较大，主要体现在几个方面:①车轮位置对U 肋对接焊缝处的疲劳应力幅影响距离较小。根据本文计算结果该细节的横向疲劳影响距离为600 mm，即车辆之间的横向距离大于600 mm 时，可不必考虑多车效应的影响。②U 肋对接焊缝疲劳损伤分布差异较大，U 肋两侧弧形段疲劳损伤较其他部位损伤严重。③随着车轮位置的改变，U 肋对接焊缝各部位疲劳损伤差异程度先急剧增大后趋于减小并最终达到稳定，e=300 mm 时疲劳损伤差异最大。

图7 U 肋对接焊缝不同部位损伤度差异变化曲线Fig.7 The difference of U-rib butt weld fatigue damage degree

3 轮迹位置对裂纹扩展的影响

随着车辆等的循环荷载作用，许多部位已经达到其损伤累计极限而产生开裂，因此长期运营阶段的正交异性钢桥面板往往带着裂纹工作，因此有必要分析车轮位置对裂纹扩展的影响。在进行裂纹扩展分析时，模型所施加的荷载依据计算应力幅，并在此基础作了适当的简化。简化结果如下:当e=0 时，由于U 肋底部各部位应力基本一致，受力均匀，可简化为均布受力状态;当e=150、300、450、600 mm时，U 肋底部应力具有二次线性分布趋势，可简化为二次线性均布受力状态;当e=750、900 mm 时，U 肋底部应力近似一次次线性分布，可简化为一次线性均布受力状态。

3.1 应力强度因子分析

构件的疲劳断裂起源于裂纹，而裂纹的静止、平衡或者发展，都与裂纹尖端应力场有直接的关系。Irwin 通过裂纹尖端应力场的研究，提出了一表征裂纹尖端应力场强度的量——应力强度因子(SIF)。应力强度因子的求解方法主要有裂纹张开位移、J 积分(J-INTEGRAL)、修正裂纹闭合积分等［10］。本文选取J 积分法计算裂纹的SIF。图8 为Ⅰ型应力强度因子分量计算结果。

图8 裂纹尖端应力强度因子KI变化曲线Fig.8 Thecrack tips stress intensity factor curve

由图8 对比同一工况作用下，不同裂纹长度对应的应力强度因子值KI可知，随着裂纹长度的增加应力强度因子KI逐渐增大，即裂纹扩展的驱动力增大，裂纹越容易发生扩展，这是由于随着裂纹长度的增加，截面承载能力逐渐退化，导致裂纹尖端应力场不断增强;同时随着裂纹的扩展，KI先急剧增加后趋于稳定，计算结果显示，当裂纹长度小于12 mm 时，KI处于急剧增加阶段，当裂纹长度大于12 mm 时，KI处于稳定增加阶段。

由图8 对比不同工况作用下相同裂纹长度对应的应力强度因子值可知，随着车轮位置的改变(e 增大)，KI逐渐减小，即裂纹驱动力减小，裂纹越难发生扩展，这是由于随着车轮的偏离，轮载局部效应逐渐减弱，使得焊缝处应力降低，导致裂纹尖端应力场强度降低。计算显示:当e≥750 时，各扩展阶段的KI基本保持一致，说明此时车轮位置对裂纹扩展的影响效应已不显著。

3.2 裂纹扩展角度分析

为了获得裂纹的扩展路径，需要确定裂纹扩展的临界条件和扩展方向，即断裂准则和扩展角。目前常用的裂纹扩展理论主要有三种:最大周向拉应力准则，最小应变能密度因子准则和最大能量释放率准则。本文选取的是最大能量释放准则，首先根据最大能量释放准则的两个基本假设［11］，即裂纹沿着最大能量释放的方向扩展以及裂纹的扩展是由于最大能量释放率达到临界值而产生的，建立裂纹扩展的基本判据。然后通过Matlab 软件建立裂纹扩展角度的平衡方程，再将每一步的应力强度子输入程序，最后通过迭代求出裂纹每一步的扩展角度。计算结果如图9 所示。

图9 裂纹扩展角度变化曲线Fig.9 The crack propagation angle curve

由图9 可知，随着裂纹长度的增加，裂纹扩展角度逐渐减小，且具有逐渐保持稳定的趋势。因此在进行裂纹修复时，比如止裂孔法，由于前期裂纹扩展角度变化幅度较大，止裂孔的方向不易确定，应尽量选择裂纹稳定扩展阶段。

3.3 裂纹扩展路径分析

为了分析车轮位置对裂纹扩展路径的影响，现根据每一步裂纹的扩展角度以及扩展长度，计算初始裂纹在各车轮荷载作用下的扩展路径，如图10 所示。

通过对比不同车轮位置作用下，整体裂纹发展形态可知:当车轮处于最不利位置时(e=0)，此时模型、荷载均对称，裂纹也沿着焊缝方向呈对称扩展;当车轮位置改变时(e ＞0)，裂纹尖端TIP1 向焊区内侧扩展，裂纹尖端TIP2 向焊区外侧扩展，整条裂纹沿初始裂纹中心呈反对称方式。

通过对比不同车轮位置作用下，每一扩展步的裂纹尖端坐标可知，随着车轮位置的改变，裂纹沿Y 方向(垂直于焊缝)的扩展增量逐渐增大，沿X 方向(平行于焊缝)的扩展增量逐渐减小，即裂纹扩展路径逐渐由与焊缝平行向与焊缝垂直过渡。如当e=150 mm时，TIP1 的X 方向坐标为-16.23，e=300 时，TIP1 的X 方向坐标为-15.94，e=450 mm 时，TIP1 的X 方向坐标为-15.8，逐渐减小;而当e=150 mm 时，TIP1 的Y 方向坐标为71.93，e=300 mm时，TIP1 的Y 方向坐标为72.71，e=450 mm 时，TIP1 的Y 方向坐标为72.9，逐渐增大。裂纹尖端TIP2扩展规律类似，在此不再赘述。

此外，对比不同车轮位置作用下的裂纹扩展路径可知，随着裂纹的扩展，当e≥750 mm 时，各工况作用下的裂纹扩展路径已趋于重合，同时结合各裂纹扩展参数的变化趋势，说明当e≥750 mm 车轮位置对裂纹的扩展已无显著影响。

图10 裂纹扩展路径Fig.10 Crack propagation path

4 结 语

本文通过有限元分析了车辆轮迹位置对江阴长江大桥U 肋对接焊缝开裂前以及开裂后的影响，得到以下结论。

①随着车轮位置的改变，U 肋对接焊缝处的应力幅逐渐减小，车轮位置与焊缝之间距离大于600 mm，可忽略车辆位置对U 肋对接焊缝开裂前的疲劳损伤累计。

②相对于其他部位，U 肋两侧弧形段疲劳损伤严重，易产生疲劳裂纹。不同车轮位置对该细节产生的疲劳损伤差异不同，当车轮位置与焊缝之间的横向距离为300 mm，所引起的疲劳损伤差异最大。

③随着裂纹扩展，应力强度因子KI逐渐增加，裂纹扩展角度逐渐减小，并最终保持稳定。计算显示:裂纹长度大于12 mm 时，处于稳定扩展阶段，疲劳裂纹修复应尽量选择稳定扩展阶段。

④随着车轮位置的改变，裂纹扩展路径逐渐由与焊缝平行向与焊缝垂直发展，车轮位置与焊缝之间距离大于750 mm 时，各扩展参数以及裂纹扩展路径趋于重合，可忽略车辆位置对U 肋对接焊缝疲劳裂纹扩展影响。

［1］ 王春生，陈艾荣，陈惟珍.基于断裂力学的老龄钢桥剩余寿命与使用安全评估［J］.中国公路学报，2006，19(2):42-48.

［2］ 曾志斌.正交异性钢桥面板典型疲劳裂纹分类及其原因分析［J］.钢结构，2011，26(2):9-15.

［3］ 吉伯海，朱伟，傅中秋，等.正交异性钢桥面板U 肋对接焊缝疲劳寿命评估［J］.重庆交通大学学报:自然科学版，2015，34(1):16-21.

［4］ GULVANESSIAN H，MENZIES J B.The eurocode for structural loading:eurocode 1［J］.Progress in Structural Engineering and Materials，2000，2(4):472-482.

［5］ JOHANSSON B，MAQUOI R，SEDLACEK G.New design rules for plated structures in Eurocode 3［J］.Journal of Constructional Steel Research，2001，57(3):279-311.

［6］ 崔冰，吴冲，丁文俊，等.车辆轮迹线位置对钢桥面板疲劳应力幅的影响［J］.建筑科学与工程学报，2010，27(3):19-23.

［7］ 周泳涛，鲍卫刚，翟辉，等.公路钢桥疲劳设计荷载标准研究［J］.土木工程学报，2010，43(11):79-85.

［8］ 荣振环，张玉玲，刘晓光.天兴州桥正交异性板焊接部位疲劳性能研究［J］.中国铁道科学，2008，29(2):48-52.

［9］ 苏益声，许安邦，陈宗平，等.钢结构脆性破坏浅析［J］.广西大学学报:自然科学版，2003，28(3):254-257.

［10］刘明尧，柯孟龙，周祖德，等.裂纹尖端应力强度因子的有限元计算方法分析［J］.武汉理工大学学报，2011，33(6):116-121.

［11］PALANISWAMY K，KNAUSS W G.On the problem of crack extension in brittle solids under general loading［J］.Mechanics today，1978，30(4):87-148.