基于Bootstrap 方法的近地风剖面参数分析
胡尚瑜,丁九成,李秋胜
(1.桂林理工大学 广西岩土力学与工程重点实验室,广西 桂林541004;2.湖南大学 建筑安全与节能教育部重点实验室,湖南 长沙410082;3.香港城市大学 土木及建筑工程系,香港999077)
随着近海岸高层建筑和高耸结构及超大跨度桥梁等工程大量的兴建,近海岸结构工程的抗风设计和安全可靠性显得尤为重要。开展强/台风作用下近地风场特性的现场实测,对近海岸工程结构抗风设计和结构安全评估有着重要的意义。近年来国内外学者[1-5]通过各种测风平台获取了大量的近地台风风场数据,探讨了台风风场平均风特性及湍流相关特性的参数取值情况,给出了相关参数的适用性;此外,一些学者[6-8]针对台风强湍流特性研究了其对建筑与结构的破坏,并取得了一些有意义的理论成果。然而受台风自身湍流结构和不同强风标准及样本统计方法等因素影响,风剖面参数存在较大变异性和不确定性。本文根据近海岸100 m 测风塔获取的2009 年台风“彩虹”和东北季风期间,10 m、50 m、65 m、80 m 和100 m 等5 个高度实测风速资料,应用Bootstrap 统计方法[10],对近海岸平坦地貌条件,台风和季风风场强风条件下平均风剖面参数和区间估计进行分析。并将实测结果与风荷载规范规定值进行比较,探讨了风荷载规范的适宜性,为近海岸工程结构抗风设计时近地风场参数的合理取值提供参考。
1 近地边界层风特性
1.1 平均风剖面
在强风作用下,近地中性稳定大气边界层的湍流主要由地面粗糙度控制,平均风速剖面变化规律常认为符合指数律或对数律[11-12]。
指数律模型:

式中:zR为参考高度,一般取10 m;Zi为任意一高度;α 为风剖面指数,α 值与地貌状况相关。对数律模型:

式中:k 为卡曼常数,取0.4;u*为摩擦速度;z0为地面粗糙度长度。
1.2 指数律模型拟合
依据指数律模型式可得:

式中:U(zi)为Zi高度上平均风速;U(zR)为参考高度ZR处平均风速;α 为风剖面指数。
根据5 个高度的实测平均风速,应用最小二乘法对风剖面指数α 进行拟合,即拟合计算风速与实测风速离差平方和趋于零可得平均风剖面指数α 的计算公式为:

各高度拟合计算风速与实测风速离差平方和计算式如下:

式中:U(z)为实测平均风速,U(zi)为拟合平均风速。
1.3 对数律模型拟合
依据对数律模型计算式可得:

式中:z0为地面粗糙度长度,其余各参数符号意义与式(3)一致。
采用最小二乘线性拟合法对5 个不同高度实测平均风速进行拟合,即拟合计算风速与实测风速离差平方和趋于零,可得地面粗糙度z0的计算公式[13]如下:

式中:z0为地面粗糙度长度,其余各参数符号意义与式(3)一致。
1.4 针对风剖面指数的Boostrap 法分析思路
选取台风和季风风场近地100 m 高度范围内的强风风速样本,采用指数律模型拟合得到各样本的风剖面指数计算序列(αs1,αs2,…,αsn)。运用Bootstrap 方法,统计分析风剖面指数置信区间的分析思路如下[14]:
①根据风速数据样本拟合得到的α 指数,记作αsi(i=1,2,…,n)。
②根据样本值X=(τ1,τ2,…,τn)=(αs1,αs2,…,αsn),计算样本均值和方差S2。
③对②中所得样本作有放回模拟再抽样:采用蒙特卡洛法随机抽出一个数据,共抽取n 次,得到第一个Bootstrap 样本X″1=(τ″11,τ″21,…,τ″n1)。
④对步骤③进行重复运作B 次,即可得到B 个Bootstrap 再生样本,用矩阵表示为:

计算再生样本的统计量:

其中:y″i=y″i1,y″i2,…,y″iB,i=1,2。
⑤根据再生样本y″i,可以得到μ 和σ2的估计:
⑥采用百分位法进行参数的区间估计:将Bootstrap 估计量θ 按从小到大排序,则置信度为1-δ 的置信区间为(kδ/2,k1-δ/2),其中kδ/2和k1-δ/2为θ^*i 的经验分位数。
2 现场实测
2.1 实测系统及场地条件
测风塔位于海南文昌木兰头近海岸,东经110°44',北纬20°09',海拔约9 m。在离地10 m、50 m、65 m、80 m、100 m 高度处分别布设安装了NRG-Symphonie 型杯式风速仪进行风速观测,同时在50 m、65 m、100 m 高度处安装了风向仪进行风向角的观测。数据测试系统采样频率为1 Hz,每10 min输出1 组平均风速风向、极大风速风向和风速、风向标准差等。观测塔观测地貌状况:东北方位来流地貌条件为海面,西南方位为平坦开阔场地,下垫面为近地2 ~3 m 高的马尾松防护林。
2.2 强风样本选取
本文以近中性条件下10 m 高度10 min 平均风速大于10 m/s 的样本为强风判定条件。台风风场风特性统计与选取样本平均风速相关,工程结构更为关注8 级大风条件下台风风场风特性。因而本文选取近海岸地貌条件下平均风速大于17.2 m/s 的台风风场强风样本,同时选取相同地貌条件下平均风速大于10 m/s 的季风风场强风样本,进行台风风场和季风风场平均风剖面统计分析。近地台风风场和季风风场观测样本的极值风速统计如表1 所示:台风“彩虹”实测3 s 最大平均风速为26.2 m/s,10 min最大平均风速为20.4 m/s。东北季风实测强风样本3 s 最大平均风速为15.9 m/s,10 min 最大平均风速为12.4 m/s。

表1 实测强风风速样本Tab.1 Filed observation of strong wind speed samples
2.3 统计样本数的影响
基于现场实测季风强风样本(样本相对较多),分别应用Bootstrap 法和经典方法对风场的平均风剖面指数α 进行统计分析,探讨分析样本容量大小对均值置信区间估计的影响。两种方法统计分析得平均风剖面指数α 均值及95%置信度条件下置信区间估计差异如表2 所示:样本容量较小(小于10 个)条件下,Bootstrap 法所得区间长度较经典方法窄,样本容量大于10 个以上时两种方法区间估计基本一致,表明在样本容量较小条件下Bootstrap 法分析结果具有较好的精度。强风条件下台风“彩虹”和季风风场样本数据,应用Bootstrap 法统计得到的风剖面均值估计的概率分布比较如图1 所示,台风风场和季风风场风剖面指数α 估计均值的样本概率分布都呈高斯分布特征,台风风场估计均值整体大于季风风场估计值,同时95%置信度条件下均值的置信区间相对窄、趋于稳定,表明强风小样本容量条件下,应用Bootstrap 方法统计分析平均风剖面α 参数分析结果具有较好的可信度。

表2 不同样本数的平均风剖面指数的均值及区间估计统计Tab.2 Statistics on mean and interval estimation of the mean wind profile index

图1 风剖面指数均值参数估计概率密度分布Fig.1 The probability density distribution about mean wind speed profile index estimations
3 风特性Boostrap 统计分析
选取实测台风“彩虹”及季风风场5 个高度的平均风速数据,应用对数律和指数律模型对风剖面进行最小二乘线性拟合。台风风场平均风剖面的拟合曲线如图2 所示。从图2 中可以看出,指数律和对数律模型都能较好的反映台风条件下近地平均风速随高度的变化规律。应用指数律和对数律模型对台风“彩虹”5 个高度变化上的平均风剖面进行拟合,得到平均风速实测值与拟合值的离差平方和分别为0.10(m/s)2和0.07(m/s)2。台风“彩虹”近地平均风剖面指数α 均值的置信上、下限曲线能较好的包络实测各高度风速比值。指数律、对数律风剖面参数拟合值如表3 所示:台风“彩虹”应用Bootstrap 法统计分析得风剖面指数α 的均值估计为0.121,95%置信度条件下的置信区间为[0.117,0.125],与我国《建筑结构荷载规范》(GB50009-2012)中A 类地貌条件风剖面指数α 规定值0.120[15]相近。季风风场应用Bootstrap 法分析得风剖面指数α 的均值估计为0.071,95%置信度条件下的置信区间为[0.065,0.070]。季风风场风剖面指数α 值小于规范推荐值和台风风场值。此外,台风风场摩擦速度及地面粗糙度长度大于季风风场。图3 给出了季风风场平均风速剖面随高度的变化情况,应用指数律和对数律模型拟合,得到平均风速实测值与拟合值的离差平方和分别为0.13(m/s)2和0.11(m/s)2。

表3 平均风剖面参数Tab.3 Parameters of mean wind speed

图2 台风彩虹平均风剖面Fig.2 The mean wind speed profiles of typhoon
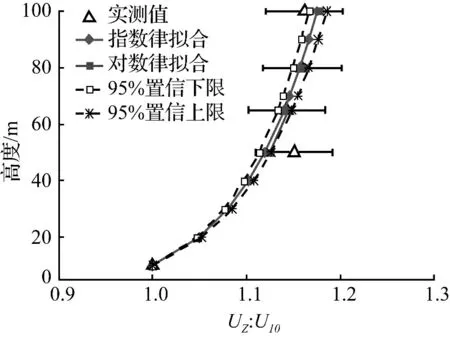
图3 季风平均风剖面Fig.3 The mean wind speed profiles of monsoon
4 结 论
本文基于选取近海岸平坦开阔地貌条件下,近地台风和季风风场强风风速样本,运用Bootstrap 方法对近地风场平均风剖面指数进行了分析,可得到如下结论:
①强风小样本容量条件下,应用Bootstrap 方法统计分析平均风剖面α 参数样本的均值概率分布符合高斯分布模型,分析结果的置信区间相对窄、趋于稳定,具有较好的精度和可信度。
②近地平均风速剖面符合指数律或对数律,应用Bootstrap 法计算得台风风场平均风剖面指数α的均值估计为0.12,与《建筑结构荷载规范》(GB50009-2012)规定值相一致;季风风场风剖面指数α的均值估计为0.07,小于规范值。台风风场摩擦速度及地面粗糙度长度大于季风风场。
致谢:感谢中国华能海南文昌风电厂提供的实测风速数据。
[1] SCHROEDER J L,EDWARDS B P,GIAMMANCO I M.Observed tropical cyclone wind flow characteristics[J].Wind and Structures,2009,12(4):349-381.
[2] 胡尚瑜,宋丽莉,李秋胜.近地边界层台风观测及湍流特征参数分析[J].建筑结构学报,2011,32(4):1-8.
[3] 宋丽莉,毛慧琴,汤海燕,等.广东沿海近地层大风特性的观测分析[J].热带气象学报,2004,20(6):731-736.
[4] 李亚春,武金岗,谢志清,等.不同强风样本湍流特性参数的计算分析[J].应用气象学报,2008,19(1):28-34.
[5] 王旭,黄鹏,顾明.台风“梅花”影响下近地风脉动特性研究[J].土木工程学报,2013,46(2):54-61.
[6] 胡尚瑜,李秋胜.低矮房屋风荷载实测研究(I)——登陆台风近地边界层风特性[J].土木工程学报,2012,45(2):77-84.
[7] 胡尚瑜,李秋胜,戴益民,等.近地台风风场特性及低矮房屋风荷载现场实测研究[J].建筑结构学报,2013,34(6):30-38.
[8] 徐 旭,李芬.玻璃幕墙在台风作用下的可靠度分析[J].广西大学学报:自然科学版,2009,34(1):22-27.
[9] EFRON B.Bootstrap methods:another look at the jackknife[J].The Annals of Statistics,1979,7(1):1-2.
[10]POWELL M D,VICKERY P J,REINHOLD T A.Reduced drag coefficient for high wind speeds in tropical cyclones[J].Nature,2003,422:279-283.
[11]CHOI E C C.Characteristics of typhoons over the south China sea[J].Journal of Wind Engineering and Industrial Aerodynamics,1978,3:353-365.
[12]ARCHER C L,JACOBSON M Z.Spatial and temporal distributions of US winds and wind power at 80 m derived from measurements[J].Journal of Geophysical Research:Atmospheres,2003,108(D9):1984-2012.
[13]蔡平,冒刘燕.基于Bootstrap 法的船闸大修间隔时间参数估计[J].珠江水运,2013,33(24):78-79.
[14]中华人民共和国住房和城乡建设部.GB 50009—2012 建筑结构荷载规范[S].北京:中国建筑工业出版社,2012.

