硅微角振动陀螺仪温度特性补偿方法研究*

余 磊， 徐大诚， 郭述文

(苏州大学 微纳传感技术研究中心，江苏 苏州 215100)

硅微角振动陀螺仪温度特性补偿方法研究*

余 磊， 徐大诚， 郭述文

(苏州大学 微纳传感技术研究中心，江苏 苏州 215100)

在研究硅微角振动陀螺结构和温度特性的基础上，创建了二元高阶多项式补偿模型，并设计了基于STM32F405的硬件补偿电路，实现该陀螺仪实时温度补偿。实验结果表明:温度补偿后的标度因数温度系数和全温零偏稳定性分别由344×10-6/℃和441°/h减小为12.6×10-6/℃和40.6°/h，使得该陀螺仪的温度特性有明显改善，验证了该补偿方法的有效性和可行性。

硅微角振动陀螺仪； 温度补偿； 标度因数温度系数； 全温零偏稳定性

0 引 言

硅微陀螺仪具有体积小、重量轻、价格低、寿命长和易批量生产等优点，广泛应用在消费电子、汽车安全系统、机器人以及惯性导航等领域[1]。温度变化对硅微角振动陀螺仪性能有较大影响，主要影响到陀螺的标度因数和零偏。对硅微陀螺的温度补偿通常有三种方法：一是利用驱动谐振频率随温度变化的关系进行自补偿[2]；二是利用品质因数的温度特性进行自补偿[3]；三是外接温度传感器进行温度补偿[4]。但是,当Q值不是很高时，前两种方法不适用。 本文是利用集成温度传感器进行补偿，使硅微角振动陀螺仪的标度因数温度系数和全温零偏稳定性提高了1个数量级，有效改善了陀螺仪的性能。

1 硅微角振动陀螺温度性能分析

1.1 硅微角振动陀螺的结构原理

单支点角振动陀螺仪结构如图1所示。陀螺工作时，由四相位驱动信号对陀螺外环进行驱动，使外环在梳齿状电极驱动下绕z轴旋转振动，当有一个绕x轴方向的角速度时，陀螺将受到一个沿y方向的科氏力作用，内盘将沿y方向左右摇摆，而摆动幅度将与科氏力大小呈正比[5]。

图1 单支点角振动陀螺仪结构模型图

角振动陀螺传递函数

|θsense(ωdriver)|=

(1)

式中 Δω=ωsense-ωdriver，为敏感与驱动的谐振频率的频差；Q为品质因数。

当Q值很大，Δf=fsense-fdriver>20 Hz，Δω≪ωdriver时，上式可以近似简化为

(2)

式中 θsense为绕敏感轴的偏转角度，Δω越小，则灵敏度越高，θdriver越大，灵敏度越高。

1.2 温度对硅微角振动陀螺仪的影响

硅微陀螺以薄硅片为材料，利用半导体加工技术制作而成，在温度变化时，结构热应力和硅材料杨氏模量的变化会影响系统刚度，而硅微陀螺的谐振频率随系统刚度变化而变化，因此，温度的变化会导致陀螺谐振频率产生漂移[6]。

材料弹性模量与温度的变化关系可用下式表示

E(T)=E0[1-α(T-T0)]，

(3)

式中 E(T)，E0分别为硅材料在温度为T，T0时的弹性模量，α为弹性模量的温度系数，系统的刚度与弹性模量呈正比

k(T)=k0[1-α(T-T0)]，

(4)

式中 k(T)，k0分别为硅材料在温度为T，T0时系统的刚度。在温度T0附近的小范围内时，谐振频率与温度线性近似关系可表示为

ω(T)=ω0[1-0.5α(T-T0)]，

(5)

式中 ω(T)，ω0分别是温度为T，T0时的谐振频率，由于温度影响谐振频率产生漂移，对陀螺驱动和检测模态均有影响[7]。

1.3 温度对标度因数和零偏的影响

谐振频率和品质因数是影响硅微陀螺性能的重要参数，标度因数和零偏是反映硅微陀螺仪性能的重要指标，其受温度的影响较大。

陀螺仪标度因数的公式如下

(6)

零偏温度系数与结构的对称性有很大的关系，因为结构设计是差分输入，具有一定的共模抑制比，与温度有关参数变化一般可以抵消掉。然而，工艺或者封装造成的结构对称性误差不可避免

(7)

这里,1/τ为各谐振模态的阻尼系数失配因子，τ= 2Q/ω为阻尼系数时间常数；θτ为阻尼轴与敏感轴的夹角。

根据式(6)、式(7)所示，影响标度因数和零偏的主要因素是谐振频率和品质因数，由1.2节可知，谐振频率和品质因数受温度的影响较大。因此，标度因数和零偏亦受温度变化的影响，随温度的变化，硅微角振动陀螺的性能变化明显，因而，有必要进行温度补偿的研究。

2 温度补偿系统设计

采用陀螺芯片内部温度传感器的输出对陀螺输出进行实时温度补偿，设计了如图2所示的温度补偿系统。

图2 温度补偿系统框图

温度补偿系统主要由陀螺和STM32F405组成。补偿参数存储在FLASH中，JTAG用于STM32F405程序的下载与仿真。在测试过程中，由于传输距离较远，采用串口传输数据。作为补偿模块，对外的接口是SPI接口。

2.1 硅微角振动陀螺仪温度建模

对陀螺的温度建模，就是要找到一个函数来较好地拟合陀螺输出与角速度输入和温度之间的曲面关系。本文采用二元高阶多项式函数对陀螺进行温度建模。

温度模型如下

(8)

式中G为输入的角速度，T为温度，F为陀螺输出值，M为多项式阶数，C为多项式系数矩阵。

系数矩阵通过最小二乘法确定其值，M的大小由补偿的精度来确定，并要同时考虑实时计算这一情况。

设有N个数据点(Gk,Tk,Fk)，要使得拟合后的总误差

(9)

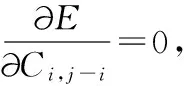
(10)

将全温下测试的数据归一化后带入式(10)中，就能计算出温度补偿模型的系数。

由表1可知，阶数越高，拟合的精度就越高，但是计算所需的时间就越长;精度越高，对陀螺的重复性要求就越高。所以,综合所有因素，采用5阶温度模型。

表1 不同阶数下拟合的误差平方和

Tab 1 Error sum squares fitted under different orders

阶数误差的平方和(((°)/s)2)30.498150.272770.177590.1040

2.2 硅微角振动陀螺温度补偿的硬件实现

硅微角振动陀螺温度补偿采用一块Cortex—M4内核的ARM芯片STM32F405RG来实现,其主频高达168 MHz，处理能力达到210 MIPS，内部带有FPU(浮点运算单元)，支持单周期DSP指令和浮点单元。

由表2可以看出:STM32F405的单精度浮点运算速度超越了DSP控制芯片TMS320F28335，完全可以用来对陀螺进行软件温度补偿。

表2 二元高阶多项式单精度浮点运算时间对比

Tab 2 Comparison of single-precision floating-point arithmetic time of binary high order polynomial

阶数STM32F103(μs)F28335(μs)STM32F405(μs)51481911106389643203549505221

STM32F405自带两个SPI接口，一个用于和陀螺交换数据，一个用于输出接口,其封装为LQFP64，尺寸为10 mm×10 mm，和陀螺芯片差不多大。将陀螺和STM32F405放在一个PCB上进行实时的温度补偿。温补后的陀螺模块可以安装在IMU上，测量三轴姿态角。

2.3 MEMS角振动陀螺温度补偿的软件实现

硬件平台搭好后，在STM32F405中编写程序，调用温度模型系数矩阵就可以对陀螺的输出进行实时的补偿。图3所示为温度补偿软件流程图。

图3 温度补偿软件流程图

陀螺数据由6个字节组成，更新速率为200 Hz。第一个字节的最高位为DATARED，当数据被读走后置0，当数据更新后又置1。角速度输出为24位有符号整形数据，温度输出为14位无符号整形数据。SPI2设置为从机模式，采用中断模式输出数据。

3 实验结果

按图4所示的系统框图对陀螺进行全温测试。测试系统基于LabVIEW开发，包括对转台和温箱的实时控制以及对陀螺的数据采集。

图4 自动化测试系统框图

对某型陀螺进行全温，±300°/s的测试。温度点顺序为85,70,60,50,40,30,20,10,0,-10,-20,-30,-40 ℃。角速度范围为-300°/s～300°/s，间隔20°/s。将得到的403个数据点带入式(10)中就可计算出温度模型的系数矩阵。

将得到的系数矩阵写入STM32F405中，对陀螺的输出进行实时的温度补偿。将陀螺模块安装在转台上，再次进行全温，±300°/s的测试，同时对原始数据和温度补偿数据进行采集,数据处理后如图5。

图5 温度补偿前后标度因数随温度的变化

由表3可以看出:非线性度、标度因数温度系数和零偏较温补前都有很大的改善。

将陀螺模块放在温箱中，在-40～60 ℃升温过程中采集陀螺的零偏数据1 h。将采集到的数据进行10 s平滑滤波后，计算均方差，就得到了全温范围内的零偏稳定性。温补前后全温零偏稳定性如表4所示。

表3 温补前后参数对比

Tab 3 Parameter comparison before and after temperature compensation

参数原始数据温补数据非线性度(10-6)<2000<100标度因数温度系数(10-6/℃)34412.6零偏均方差((°)/h)748.8962.29

表4 温补前后的全温零偏稳定性(-40～60 ℃)

Tab 4 Full-temperature zero bias stability before and after temperature compensation

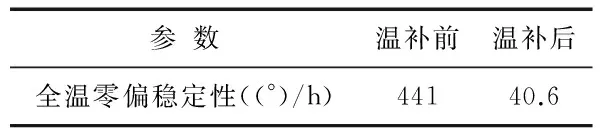
参数温补前温补后全温零偏稳定性((°)/h)44140.6

从图6可以看出:温度补偿后，陀螺的零偏输出已没有了明显的波动，零偏稳定性下降到40.6°/h。当然，如果考虑温度变化速率，建立动态温度模型，零偏稳定性还能有更大的改善。

图6 温补前后全温范围零偏的对比

4 结 论

本文在分析硅微角振动陀螺结构的基础上，着重剖析

了由温度变化引起角振动陀螺谐振频率、标度因数和零偏的漂移，进而对陀螺的温度特性进行了建模和仿真。在此基础上，设计了基于STM32F405的硬件补偿电路和软件算法，并进行了补偿前后性能测试对比分析。实验结果表明:补偿后的标度因数温度系数提高了27倍，全温零偏稳定性降低10.8倍，明显优化了陀螺的温度特性，证明了该补偿方案的有效性。

[1] 赵晓辉，伊国兴，王常虹.硅微陀螺温度漂移补偿研究[J].传感器与微系统，2008,27(10)：48-50.

[2] 满海鸥，肖定邦，吴学忠，等.基于驱动频率的硅微陀螺零偏补偿方法研究[J].传感技术学报，2012,25(5)：624-627.

[3] 杨 亮，苏 岩，裘安萍，等.高品质因数微机械陀螺的温度自补偿[J].光学精密工程，2013,12(11)：2870-2876.

[4] 陈湾湾，陈智刚，马 林，等.MEMS微机械陀螺温度特性分析与建模[J].传感技术学报，2014，27(2)：194-197.

[5] 赵晓辉，伊国兴，王常虹.硅微陀螺温度漂移补偿研究[J].传感器与微系统，2008,27(10)：48-50.

[6] Bongsang Kim,Chandra Mohan Jha.Temperature dependence of quality factor in MEMS resonator[C]∥MEMS2006,Istanbul,Turkey,2006:590-593.

[7] 柳小军，杨 波，袁安富，等.基于集成温度传感器的硅微陀螺仪数字化温度补偿研究[J].传感技术学报，2014,72(6):770-774.

徐大诚,通讯作者,E—mail:xudacheng@suda.edu.cn。

Research on compensation method of temperature characteristics for silicon micro angular vibration gyroscope*

YU Lei, XU Da-cheng, GUO Shu-wen

(Micro-nano Sensor Technology Research Center,Soochow University,Suzhou 215100,China)

A binary order polynomial compensation model is set up based on analyzing the structure and temperature characteristics of the silicon micro angular vibration gyroscope,and the hardware compensation circuit is designed based on the STM32F405,realize real-time temperature compensation of the gyroscope.Experimental result show that through compensation method proposed,the temperature coefficients of the scale factor and stability of full-temperature zero bias decrease from 344×10-6/℃ and 441°/h to 12.6×10-6/℃ and 40.6°/h,respectively,the temperature characteristics of the gyroscope is significantly improved and effectiveness and feasibility of the compensation method is verified.

silicon micro angular vibration gyroscope; temperature compensation; temperature coefficients of scale factor; stability of full-temperature zero bias

2015—02—15

国家自然基金重点资助项目(61434003)

10.13873/J.1000—9787(2015)11—0026—04

U 666.1

A

1000—9787(2015)11—0026—04

余 磊(1990-)，男，江苏常州人，硕士研究生，主要研究领域为MEMS惯性传感器性能测试与补偿。