电工钢片磁化曲线无损检测传感器研究

冉 祎， 谢 岳

(中国计量学院 机电工程学院，浙江 杭州 310018)

电工钢片磁化曲线无损检测传感器研究

冉 祎， 谢 岳

(中国计量学院 机电工程学院，浙江 杭州 310018)

针对一种电工钢片磁化曲线无损检测传感器进行研究，该传感器利用磁通测量线圈和磁位计分别检测电工钢片特定区域的磁通和磁势，实现钢片磁化曲线的无损检测。为了实现传感器的优化设计，利用ANSYS软件对传感器进行二维和三维仿真实验。同时，通过仿真实验获得不同励磁载荷情况下磁通测量线圈和磁位计的仿真测量值；对检测到的信号进行曲线拟合，求得被测电工钢片的基本磁化曲线。仿真实验验证了该传感器检测方案的正确性和优化设计的可行性，并为实际应用提供了根据。

电工钢片； 磁化曲线； 无损检测； 传感器

0 引 言

电工钢片是一种基础电工材料，它被广泛地用作各类电动机、发电机和变压器的铁芯。为了合理地设计这些电气产品，就必须准确地获取电工钢片的基本磁化曲线[1]。目前，在电工钢片基本磁化曲线的检测方法中爱泼斯坦方圈法应用最为广泛，但它需要裁剪规定尺寸的钢片样片并搭建铁芯试样，因此,费时费料。而且它需要估算等效磁路长度，这对实验结果的准确性有一定的影响[2,3]。日本工业标准提出的单片测量法直接检测钢片试样的磁通密度和磁场强度，避免了等效磁路长度的计算并提高了测量准确度，但仍需对试样进行裁剪[4]。电工钢片无损检测传感器具有灵活机动和测量准确的特点，且避免了对试样进行裁剪的缺点[5]，但是采用传统理论计算方法无法准确地计算传感器的电磁场分布情况，因此，无法准确设计传感器。

本文利用ANSYS软件对电工钢片无损检测传感器进行优化设计，解决该传感器目前设计存在的不足，同时通过仿真计算被测电工钢片的基本磁化曲线。仿真结果验证了该传感器和优化方案的可行性和正确性。

1 无损检测传感器结构与检测原理

1.1 传感器基本结构

传感器的结构如图1所示，主要由磁轭、励磁线圈、磁通测量线圈及磁位计构成，检测时传感器放在被测钢片上。磁轭由内圆柱磁轭、外圆柱磁轭和圆柱体磁轭盖紧配构成。励磁线圈和磁通测量线圈绕在内圆柱磁轭上，磁通测量线圈紧靠被测电工钢片一侧。多个串联在一起的磁位计按辐射状均匀地分布在测量区域平面内，该平面紧贴被测电工钢片。

图1 无损检测传感器基本结构

1.2 检测原理

在实际工作中，由于内、外圆柱磁轭靠近钢片部分的表面存在一定厚度的涂层与被测电工钢片表面平整度的影响[6]，传感器与被测电工钢片是不可能紧密贴牢的，因此，这一段磁路可以等效为气隙。磁轭、气隙和电工钢片形成了闭合磁路，励磁线圈产生工作磁通Φ(t)，Φ(t)由磁通测量线圈检测。根据磁场强度在两种磁介质的交界面上切向分量连续的条件，磁位计所测得的磁势就是电工钢片从r1到r2的磁势。

在保证磁通Φ(t)为正弦波的前提下，当Φ(t)取得峰值Φm时，电工钢片不同r处的磁感应强度B和磁场强度H也达到最大值，它们处于交流磁滞回线的顶点，即基本交流磁化曲线上。设t=t1时，Φ(t)=Φm，F=Fm，则对任意时刻t有

(1)

式中eΦ(t)为磁通测量线圈的感应电动势，eF(t)为磁位计的感应电动势，N为磁通测量线圈匝数，S0和n0分别为磁位计的截面积和单位长度匝数，μ0为真空磁导率。

电工钢片的基本磁化曲线采用如下函数逼近[5]

(2)

式中fi(B)为已知函数，ai(i=0,1,…,n)为n+1个待定系数。钢片不同r处的磁感应强度B为

(3)

由式(2)和式(3)可得

(4)

因此,被测电工钢片从r1至r2的磁势最大值为

(5)

式中r1和r2为已知量，当Φm已知时，fi(r,Φm)也是已知量。调节励磁线圈的电流，可以得到不同的磁通峰值Φm和磁位差峰值Fm。将获得的p+1组(Φm.k,Fm.k)(k=0,1,…,p,p>n)代入式(5)，可得以下超定方程组

(6)

2 传感器仿真实验

2.1 仿真模型建立

在仿真研究中，采用武钢生产的50W470型电工钢片作为被测电工钢片，其基本磁化曲线如图2所示。磁轭采用基本磁化曲线如图3所示的具有高磁导率的纳米晶合金，以保证整个磁轭各部分工作在非饱和区域。

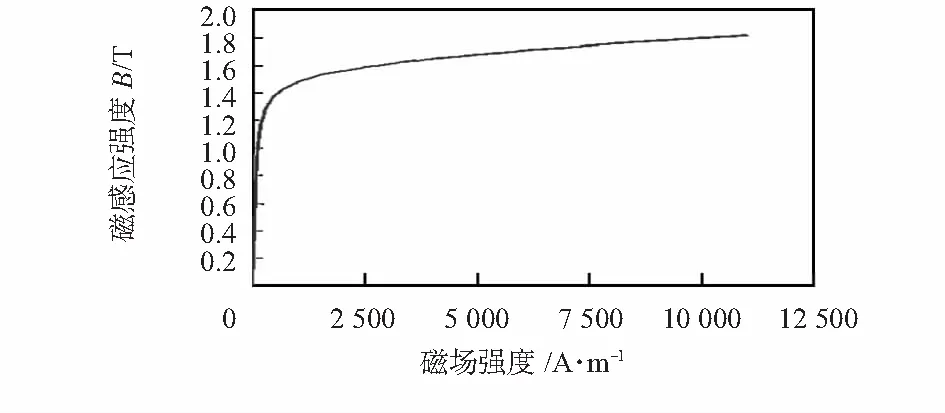
图2 电工钢片基本磁化曲线

图3 磁轭基本磁化曲线

图4和图5所示分别为传感器的二维和三维仿真模型，与二维仿真模型相比，三维实体仿真模型添加了磁通测量线圈和磁位计。传感器有多个串联的磁位计按辐射状对称且均匀地放置在r1≤r≤r2区域。为了简化，仿真时仅放置一根磁位计来测量磁势。

图4 二维仿真模型

图5 三维实体模型

2.2 仿真结果分析

经过多次仿真计算，确定了如表1和表2所示的一组传感器结构尺寸和线圈参数。

表1 测量传感器结构尺寸

Tab 1 Structure size of measured sensor

参数尺寸(mm)参数尺寸(mm)磁轭盖高h1 5外磁轭内径r370内、外磁轭柱高h280外磁轭外径r480内磁轭内径r0110磁位计测量区域内径r138内磁轭外径r0220磁位计测量区域外径r258

表2 线圈参数

Tab 2 Coil parameters

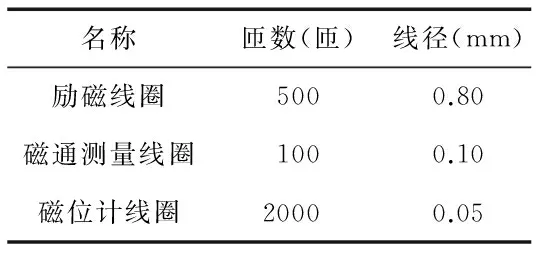
名称匝数(匝)线径(mm)励磁线圈5000.80磁通测量线圈1000.10磁位计线圈2000 0.05

由装置结构可知，气隙漏磁是影响传感器测量误差的主要因素，在确定传感器结构尺寸的基础上，变化气隙δ的厚度，通过电工钢片在测量区域内达到最小磁感应强度0.4 T和最大磁感应强度1.8 T两种情况的二维仿真进行分析。图6所示为传感器磁力线分布图，图7所示为气隙δ分别取0.01，0.04，0.1 mm时被测电工钢片与气隙处磁力线的分布图。由图6和图7可以看出传感器内部的磁场大致分布情况。当气隙δ的厚度不断增大时，气隙处磁力线分布外扩情况越来越严重，漏磁越来越大。

图6 磁力线分布图

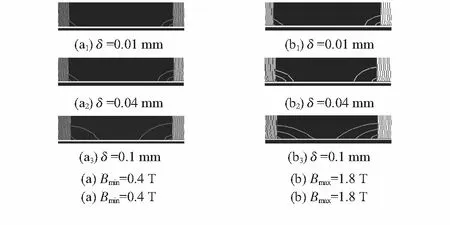
图7 被测电工钢片与气隙处磁力线分布图

考虑到电工钢片表面的涂层厚度、纵向厚度偏差及图7的仿真结果，设计时气隙δ不大于0.04 mm较为合适。而对于磁通测量线圈，由图6、图7(a2)和图7(b2)可知，将其上移以避开气隙漏磁，就可至它的合适位置。当δ=0.04 mm，励磁线圈加载幅值为9.6～62 V的工频正弦励磁电压，可实现电工钢片上磁感应强度B为0.4～1.8 T。调节不同的励磁电压，可获得由磁通测量线圈与磁位计测得的电工钢片中r1≤r≤r2区域内的多组磁通Φm与磁势Fm仿真值，表3所示为几组典型测量值。图8所示不同励磁电压幅值时为Φm和Fm的测量仿真值与电工钢片为r1≤r≤r2区域中Φm和Fm理论值的相对误差曲线，由于存在漏磁，Φm和Fm的测量仿真值总比理论值要小。由图8可见，磁通测量线圈的Φm测量仿真误差在-0.5 %左右，磁位计的Fm测量仿真误差在-0.8 %左右，从而证明无损检测传感器的两个检测线圈都具有较高的检测准确度。

表3 磁通Φm和磁势Fm仿真值

Tab 3 Simulation value of magnetic flux and magnetic potential

励磁电压(V)磁通Φm(10-4Wb)磁势Fm(A)励磁电压(V)磁通Φm(10-4Wb)磁势Fm(A)9.60.72891.2735221.64283.9896110.83641.4108241.73895.2796121.06951.7332261.80556.7454131.16931.9086291.897410.2338151.29632.1932342.018819.4731171.39262.4882422.051023.0605201.56243.3235502.102630.3446211.60523.6471622.148938.2207

图8 Φm和Fm的测量误差

3 基本磁化曲线的求取

利用式(1)～式(6)并结合Matlab软件中的Polyfit函数对仿真测量所得的多组Φm和Fm数据进行最小二乘分段曲线拟合[7]，从而求得电工钢片的基本磁化曲线。图9所示为仿真测量基本磁化曲线与图2所示的标准曲线的比较图，可见两条曲线吻合度很高。图10所示为基本磁化曲线测量相对误差，相对误差在1 %左右。结果表明：该传感器具有较高的测量准确性。

图9 仿真结果与标准值比较图

图10 H测量值的相对误差

4 结 论

本文针对一种电工钢片磁化曲线无损检测传感器进行

研究。利用ANSYS有限元分析软件合理设计传感器，并通过仿真实验得到不同励磁载荷情况下磁通测量线圈所测的磁通和磁位计所测的磁势，结果表明:两个检测线圈测量误差分别在0.5 %,0.8 %左右。最后通过曲线拟合方法求出被测电工钢片的基本磁化曲线，其误差较标准曲线达到1 %左右，因此,传感器具有较高的准确性，这也验证了检测方案的正确性，为传感器实际应用提供了根据。

[1] 邓 聘.硅钢材料的磁化特性及其磁路分析的研究[D].北京:华北电力大学,2012.

[2] GB/T 3655—2008.用爱泼斯坦方圈测量电工钢片(带)磁性能的方法[S].北京:中国标准出版社,2009.

[3] Marketos P,Zurek S,Moses A J.A method for defining the mean path length of the epstein frame[J].IEEE Trans on Magnetics,2007,43(6):2754-2757.

[4] Japanese Industrial Standards Committee.JIS C 2556 Methods of measurement of the magnetic properties of magnetic steel sheet and strip by means of a single sheet tester[S].Tokyo:Japanese Industrial Standards Committee,1996.

[5] 谢 岳,钱克猷,江传桂.一种新型电机用的电工钢片磁性能无损检测传感器[J].计量技术,2000(4):33-37.

[6] GB/T 2521—2008 冷轧取向和冷轧无取向电工钢带(片)[S].北京:中国标准出版社,2009.

[7] 陈仁生.DW470—50硅钢片磁化曲线的曲线拟合[J].中小型电机,1997,2(4):13-15.

Research on nondestructive testing sensor of magnetization curve of electrical steel sheet

RAN Yi, XIE Yue

(College of Mechanical and Electrical Engineering,China Jiliang University,Hangzhou 310018,China)

A nondestructive testing sensor for magnetization curve of electrical steel sheet is studied，magnetic flux and magnetic potential in a particular area of steel are measured by magnetic flux measurement coil and magnetic potentiometer in the sensor to achieve nondestructive testing of magnetization curve of the steel.2D and 3D simulation experiments of the sensor are carried out through ANSYS software,the sensor is optimally designed.Meanwhile,the measured value of magnetic flux measurement coil and magnetic potentiometer under different excitation loads are calculated by simulation experiments;basic magnetization curve of electrical steel sheet is obtained by curve fitting method for the detected signal.The simulation experiments verify the correctness of the sensor detection scheme and the feasibility of the optimization design,and provide basis for practical application.

electrical steel sheet; magnetization curve; nondestructive testing; sensor

2015—03—06

10.13873/J.1000—9787(2015)11—0059—04

TP 211

B

1000—9787(2015)11—0059—04

冉 祎(1990-)，女，侗族，贵州铜仁人，硕士研究生，研究方向为检测技术与自动化装置。