单元复习，提高学生思维的灵活性

浙江富阳市富春五小（311400） 邱春礼

单元复习，提高学生思维的灵活性

浙江富阳市富春五小（311400） 邱春礼

在单元复习课中，尝试通过多元表征，引导学生构建知识网络，并对知识与技能、策略与方法的选择和应用作出指导，提高学生思维的灵活性。

数学教学 复习 灵动 单元 思维

一、习题——引发思考

1.现象

在一次练习中，分散编排着几道习题，如下。

（1）直径比是2∶1，周长比是（ ），面积比是（ ）。

（2）大圆半径等于小圆直径，周长比是（ ）。

（3）大圆半径等于小圆直径，周长和是18．84厘米，大圆周长是多少厘米？

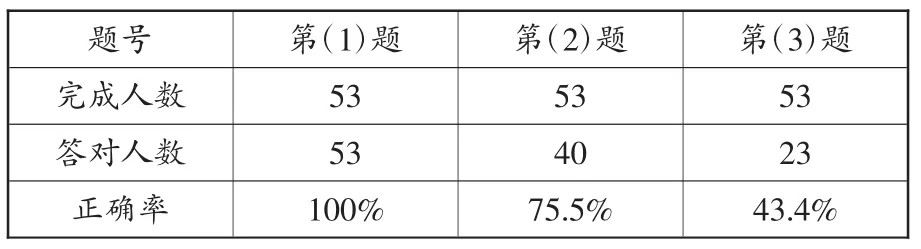
前几节课引导学生从比的角度认识圆的半径、直径、周长、面积之间的关系，但由于是分散学习的，所以希望通过本次的变式练习，增强学生从比的角度去思考并解决问题的意识。但是，从批改学生的练习结果（见下表）来看，情况不容乐观。

?

为此，我访谈了几位做错的学生。

生1：我在做第（2）题时，自己假设了一个大圆的半径为1厘米，小圆半径则为0．5厘米，最后算错了。

生2：我做第（3）题时，假设不出来，乱写的。

生3：我下课与同学交流，才发现用比来做这么简单，自己当时没想到。

……

从上面的访谈中可以看出，学生在解决第（2）和第（3）题的过程中，并没有想到前面小结过的知识。也就是说，第（1）题正确率为100%，更多的是来自于学生的背诵与记忆。

2.思考

郑毓信教授认为：“在解题或新的数学学习活动中，学生往往不善于在心理表征的不同侧面之间进行转换，从而也就不能很顺利地去找出对于求解目前所面临的问题较为适合的成分。”林崇德教授则认为：“数学思维的灵活性，这是学生在数学思维活动中，思考的方向、过程与思维技巧的即时转换科学性水平的集中反映。”由此可以看出，数学教学应当帮助学生学会在同一概念的不同心理表征或概念意象的不同侧面之间灵活地实现转移。我认为，这一任务落实在单元复习课中是比较合适的，因为单元复习课主要有三个功能，即知识整理、查漏补缺、思维提升，这三个功能不是单独的个体，而是相互联系、相辅相成的。依据“艾滨浩斯遗忘曲线”理论，一个单元的学习时间跨度刚好处在复习的最佳时机。

二、实践——让复习走向灵动

1.多元表征，构建网络

新人教版小学数学六年级上册教材安排了分数乘法、分数除法、比、百分数等内容，与学生在五年级学习分数的意义、四年级学习小数的意义等内容紧密相连，但由于每个单元有自己的侧重点，而且时间跨度又大，所以给学生的感觉是零散的。同时，教材的编排是螺旋上升的，知识之间是紧密联系的，不过这些前后联系紧密的数学知识由于所处的学习阶段不同，其表征也就不同。教学实践表明，知识表征的不同，往往会误导学生，让他们觉得这些知识表征之间是没有任何联系的，从而在学习中不能灵活地提取与选择合适的信息进行加工。

认知心理学认为：“信息以图式的方式表征，将大大提高其激活和提取的速度，也会节省极为有限的工作记忆的存储空间。”所以，在教学“百分数（一）”的单元复习课中，我做了以下的探究。

（1）文字表征。

师（呈现信息：男生人数比女生少20%）：请你说一句话，这句话所表达的意思要跟大屏上呈现的信息一样，看谁想到的句子多。（先让学生静静地思考，交流反馈）

生1：男生人数是女生人数的80%。

生2：男生人数是女生人数的0．8倍。

生3：男生人数与女生人数的比是4∶5。

……

通过变换句式，学生很快将百分数、分数、小数、比这些概念联结起来，加深了对概念的理解。但是，我们从中也发现，受呈现信息的影响，学生的反馈大都呈现同样一个模式，这对于学生思维灵活性的发展是不利的。

师（适时引导）：大家说的都是谁与谁在比？

生4：男生人数和女生人数在比。

师：还可以怎么比呢？

生5：女生人数和男生人数比。

师：那么，这句话的意思还可以怎么表达？

生6：女生人数是男生人数的125%。

生7：女生人数比男生人数多

生8：女生人数是男生人数的1．25倍。

生9：女生人数与男生人数的比是5∶4。

……

当学生能用不同的数来表达的时候，说明学生对数的理解已经不是单一的、片面的，而是形成了一个整体的知识网络。郑毓信教授曾指出：“数学教学不应求全，而要求联。”这就要求教师不仅要关注知识点的教学，更要重视沟通知识点之间的内在联系，引导学生自主建构数学知识网络。

（2）算式表征。

有了对数的意义的深刻理解，学生再来用等式表达，就比较得心应手了。

师：你能用等式表示这句话的意思吗？

生10：女生人数×20%＝相差数，女生人数×（1－20%）＝男生人数。

生11：女生人数×＝相差数，女生人数×（1－）＝男生人数。

生12：女生人数×0．2＝相差数，女生人数×（1－0．2）＝男生人数。

生13：总人数×＝女生人数，总人数×＝男生人数。

师：仔细观察，大家写的等量关系有什么相同的地方？

生14：都是乘法，一个数乘分率或倍数等于另一个数。

……

这里，既将“比一个数多（少）百分之几”纳入“一个数是另一个数的百分之几”的认知结构中，又将“一个数是另一个数的百分之几”纳入“一个数是另一个数的几分之几”和“一个数是另一个数的几倍”的认知结构中，形成概念系统，使学生了解有关概念之间的逻辑关系，从而实现概念的融会贯通。

（3）图形表征。

师：你还能用图形来表示这句话的意思吗？（学生动手画一画后交流反馈）

……

为了让学生的思维灵活起来，数学教学要引导和促进学生在同一数学概念心理表征的不同成分之间作出灵活的转移。概念的外部表征，算式的符号化，丰富了学生内在的思维结构，为灵活解决问题和学习新知识提供了可能。

2.精选素材，有效指导

有了丰富的知识储备，学生在面临比较单一的问题时，知识的提取与应用不存在太多的问题，甚至有很多单一的技能已经达到了自动化的程度，如基本的口算等。但遇到稍难一点的问题或学习新知识时，学生在提取的过程中还是会出现困难，这是因为学生不善于搜索，缺乏搜索的路径与方法。所以，教师要设计好相关练习，通过课堂的有效指导，让学生积累灵活解决问题的经验。

（1）知识技能的综合运用指导。

新人教版小学数学六年级上册第二单元“位置与方向（二）”主要学习用方向和距离两个要素确定位置，由于这是四年级学习过的知识，所以教材补充了“用数对确定位置”的内容。相对简单的知识点如何丰富它的内涵，让学生积累灵活解决问题的经验呢？仔细分析后发现，我们可以把这一内容放到大背景下，也就是放到“图形与几何”的领域之中引导学生进行探究。“图形与几何”领域分为“图形的认识”“图形的测量”“图形的运动”“图形与位置”四个板块的知识，怎样的习题可以承载这么重要的学习任务呢？一份毕业卷上的一幅图（见右图）引起了我的注意。在单元复习中，我以此图为例，让学生画一个与△ABC面积相等的三角形，并用数对表示出它三个顶点的位置，然后思考：“在画的过程中，你用到了哪些知识？”我让学生在独立思考后进行反馈，反馈时侧重于画法，数对表示顶点的教学就一带而过了。

生1：我测量了它的底和高，底是5厘米，高是2厘米，于是我画了一个底是5厘米、高是2厘米的三角形。

生2：我是将这个三角形向右平移5格来画的，因为平移后的图形形状、大小不变。

生3：我是将这个三角形绕点B顺时针方向旋转90度来画的，因为旋转后的图形形状、大小也不变。

生4：我是用轴对称来画的。

生5：我是将点C向右平移一格来画的。

师（小结）：利用这些知识，我们还解决过哪些问题呢？

……

以这一习题为载体，通过回忆学过的基础知识与基本技能，把一个个零散的知识点串联起来，培养了学生解决问题的能力。

（2）策略方法的综合运用指导。

在五年级“长方体和正方体”的单元复习中，我以下图为例，让学生用多种方法解决问题。

师：以正方体与长方体的组合为例（如下图），想一想，你有几种方法来求它的体积？请你用算式表示出来。（右边方框内是当时的板书）

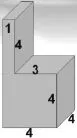
（先让学生独立思考，再请几个学生板演，学生出现分割、填补、平移这三种方法）

师：观察黑板上的算式，你都明白同学的算法吗？（指名学生边说边用课件演示，让所有学生明白每个算式的意思）

师：根据算法的特点，我们可以给它们取个名字。（板书：分割、填补、平移）为了丰富同学们解决问题的策略（板书对称扩大和倍比关系这两个算式），请同学们观察并思考这两个算式的算理。你能看懂吗？

……

师：这些方法与策略不仅仅可以用来解决立体图形的体积问题，在平面图形、数与代数领域中也有用武之地。老师以扩大法的运用为例，抛砖引玉，希望能给大家一些启发，我们一起来看一看。（课件呈示如下，学生自由阅读与理解）

①扩大法在平面图形练习中的应用。

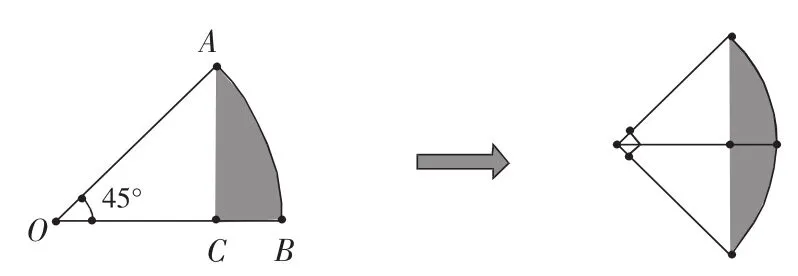
下图中扇形的半径为6厘米，圆心角为45度，AC垂直于OB，垂足为C，阴影部分的面积是多少平方厘米？

分析：将图以OB为对称轴画出它的轴对称图形，如下图所示，这样左图阴影部分的面积为（π×62÷4－62÷ 2）÷2＝5．13（平方厘米）。

②扩大法在数与代数中的应用。

鸡兔共8只，有22只脚，鸡兔各有多少只？

用□表示鸡的只数，用○表示兔的只数，根据已知条件发现如下。

将（1）乘2（扩大到原来的2倍），得：

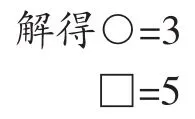
对比（2）与（3），得2○＝22－16。展示多种解题策略与方法的主要目的在于引导学生学会从多角度看问题，积累运用多种策略解决问题的数学活动经验，并指导学生学会将策略应用到其他知识领域，明白这些策略的使用范围。这样教学，既拓宽了学生的视野，又提升了学生的思维能力。

总之，提高学生思维的灵活性，不仅要让学生学会使用各种具体的认知策略，更重要的是要让学生懂得应该在何时何地使用何种策略，提高学生的元认知水平。

（责编 蓝 天）

G623.5

A

1007-9068（2015）26-019