电网企业多区域多时段多品种购电组合优化模型研究

陈 坤,谭忠富,戈 通,黄锦鸿,陈守军

（1.广州供电局有限公司,广东广州 5lO62O；2.华北电力大学能源环境与经济研究所,北京 lO22O6）

文章编号：lOO7-2322（2Ol5）O6-OO79-O7 文献标志码：A 中图分类号：F425

电网企业多区域多时段多品种购电组合优化模型研究

陈 坤1,谭忠富2,戈 通2,黄锦鸿2,陈守军2

（1.广州供电局有限公司,广东广州 5lO62O；2.华北电力大学能源环境与经济研究所,北京 lO22O6）

0 引 言

电力需求量随着经济增长而不断增加,电网企业的售电收益对电价的变动越来越敏感,电价的波动对电网企业收益将产生巨大影响,因此考虑电网企业收益,必须考虑电价及其波动。同时,随着市场机制的引入,电力市场领域产生了多种电价及购电模式。目前,国内购电市场主要有合同市场、现货市场以及辅助服务市场,国外还有期权和期货市场［1］。其中合同市场分为长期合同和中期合同,现货市场有日前交易市场和实时交易市场。由于合约规定了交割时的价格,因此合约市场风险较小,可以为电网企业提供稳定价格的电量；现货市场电价波动较大,可能给电网企业带来较高的收益,但风险较大。电网企业往往参与多种交易,即既参与合同市场,也参与现货市场；既参与本地购电,也参与跨区域购电,希望通过这种方式实现风险最小而收益最大。电力公司如何安排跨区域多品种购电,实现风险和收益综合最优已成为热门研究课题。

国内外文献对发、输、配、送环节电量分配和风险评估优化方面已做了大量研究［1-l4］,涉及方法包括①均方差法［2］；②均半方差法［3-5］；③收 益 方差法［6,7］；④在险价值VAR［8-lO］；⑤条件在险价值CVAR［11-l3］；⑥普风险度量［l4］。这些文献中,多数文献只对单一时段做研究,但实际上电网企业购电决策是多时段问题,上期决策可能影响下期决策；其次,多数文献在构建模型时,假设市场电价有确定的分布,这使模型局限性增大；最后,由于市场机制不是完全开放的,电网购电时往往受到政策、环境等各方面因素的影响,购电不是完全市场化,受到各种各样的约束影响,多数文献都未予以考虑。

基于以上研究,本文以现代资产组合理论为基础,建立电网企业多区域多时段多品种购电优化模型,解决以下3个问题:①考虑电网购电是一个长期过程,研究多时段购电决策,考虑上期购电对本期的影响；②考虑电网购电时的实际约束条件,研究不完全市场化下电网的最优购电决策；③研究如何改善这些约束才能使电网购电最优。

1 电网多品种购电收益与风险的表示

现代投资组合理论常用期望表示收益,用方差表示风险。设 K表示电网多市场购电的组合，E（rK）表示在 K中购电的期望收益,σ2K表示在 K中购电的方差。则根据投资组合理论,电网企业的收益表示为

其风险表示为

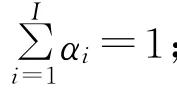
2 电网多品种购电收益与风险关系分析

2.1 两个市场的情形

设电网向A、B两个市场购电,αA表示向A市场的购电比例,αB表示向B市场的购电比例；则有:αB=1—αA；代入（1）（2）有

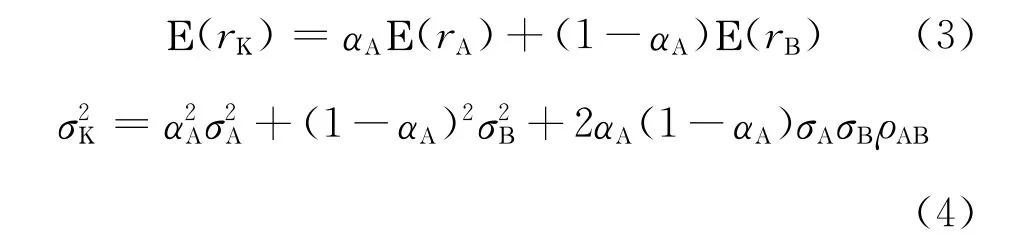
由（4）式知,电网购电风险与A、B市场的相关系数有关,在此进行分类考虑:

①当A、B市场正相关时,即ρAB=1,此时式（4）化简为

可见,E（rK）、σK均与αA呈线性关系,故E（rK）、σK也呈线性关系,风险收益轨迹如图1（a）所示。

②当A、B负相关时,即ρAB=—1,此时式（4）化简为

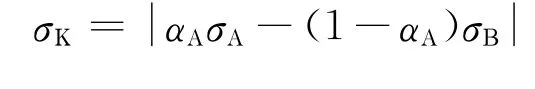
可见,E（rK）、σK呈分段线性关系,风险收益轨迹如图1（b）所示。

③当A、B不相关时,即ρAB=O,此时式（4）化简为

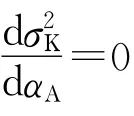
④一般情形

由①、②、③知相关系数ρAB决定了风险收益曲线的弯曲程度。随着ρAB的增大,弯曲程度将变小。当ρAB=1时,弯曲程度最小,呈直线；当ρAB=—1时,弯曲程度最大,呈折线；不相关是一种中间状态,比正完全相关弯曲程度大,比负完全相关弯曲程度小,中间的3条曲线依次为—1＜ρAB＜O、ρAB=O、O＜ρAB＜1,如图1（d）所示。

图1 ρAB取不同值时收益风险关系

2.2 多种市场的情形

由2.1知只要不是正负相关,两两购电市场组合风险和方差关系均为曲线。当存在多个市场时,可以看作是两两市场组合的再组合。此时多市场组合收益风险的轨迹为再组合后围城的区域,也是曲线构成,其形状如弹头型,如图2所示（假设从A、B、C 3个市场购电）。

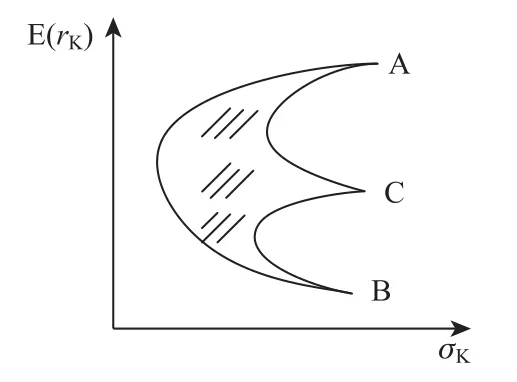
3 电网多区域多品种购电有效边界及其数学模型

3.1 电网多区域多品种购电有效边界

电网公司具有一般的偏好规则:当风险一定时,希望收益越大；当收益一定时,希望风险越小。所以,在决定购买量时,收益风险轨迹的上边界总是优于内部区域和下边界的。将收益风险轨迹的上边界定义为该市场组合的有效边界（Efficient Frontier）。最优的市场组合,总是在有效边界上产生,并且有效边界上的不同点,没有优劣势之分,选择与否只与电网企业的无差异曲线有关。

3.2 有效边界的数学模型

设电网跨区域从多品种市场组合K购电,K中包含n个不同区域不同品种的购电市场,其期望收益率为R=（r1,r2,...,rn）T,方差-协方差矩

区域D的边界不能直观地表示出来,但可以定义:

①风险一定的条件下,最大收益的组合；②收益一定的条件下,最小风险的组合。

而区域D的有效边界是只满足①的所有组合。条件①可以表达为以下约束问题的解:

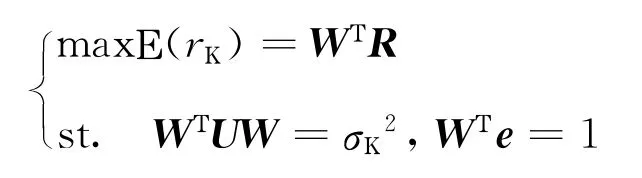
引入两个拉格朗日乘子,构造拉格朗日函数: 1（W,λ1,λ2）=WTR+λ1（σT2—WTUW）+λ2（1—WTe）

令:

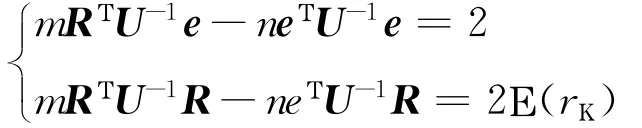
令a=RTU—1R,b=RTU—1e=eTU—1R,c= eTU—1e,则ac—b2＞O,且a＞O,b＞O,可解得

于是,

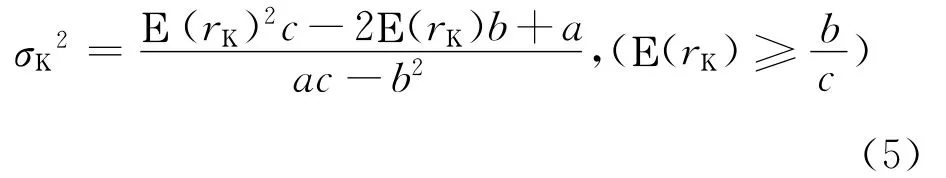
可知,区域D的有效边界为双曲线的上半部分。（详细推导见附录）

4 电网多区域多时段多品种购电优化模型

4.1 无约束下的购电优化

电网在有效边界上的购电组合均为最佳组合,选择与否只与电网公司的无差异曲线有关。故理论上电网最佳购电组合只需要满足（1）、（2）、（5）式。此时,求无约束购电最优,可以调用matlab金融工具箱中的frontcon函数来实现优化。

4.2 实际约束及含约束的购电优化

由于存在实际约束,并不是所有有效边界上的购电组合都具有实际意义。电网购电具有以下约束条件。

4.2.1 购电稳定性约束

式中:Δαi表示针对上期的购电比例增量,表示购电比例增量下限,表示购电比例增量上限。电网公司购电决策是多时段问题,上期决策可能影响下期决策,这种影响充分考虑了市场稳定性。各购电市场本期购电变化增量应控制在合理范围内,购电增量越小,越利于市场稳定。

4.2.2 负荷预测精度约束

实际上,由于负荷预测精度不能达到lOO％,总有一小部分电量从实时市场购买,这部分电量作为战略性调控电量是不可缺少的。实时电价波动剧烈,而且调控电量易变,很难控制,一般来说,进行优化的电量是不包括实时电量的。

4.2.3 现货市场最低比例约束

从合约市场购电目的是为了规避现货市场交易风险。当现货市场价格期望较高时,电网往往会选择在合约市场购买全部电量,这时遇特殊情况（如预测估高,电量过剩）将给电网带来巨大损失,这反而增加了电网风险。故即使期货市场价格较低,电网也会保留一部分现货市场电量。保留现货市场电量的比例,与电力负荷预测的能力相关。这里假设现货市场购电量不低于总电量的k倍,α1表示现货市场购电量。

4.2.4 其他实际约束

不同地区、政策、环境以及市场特性带来的其他约束。根据实际情况考虑的一些没有共性的特殊约束。比如地区不同装机容量限制不同,可能本地负荷不能满足本地需求,必须从外地市场购电,这就对不同市场的购电比例构成了约束。虽然约束不同,但这些约束都是对相关市场购电比例进行限制的。

由于实际购电约束的存在,满足公式（1）、（2）、（5）的理论最优购电比例并不一定存在。这时可以调用matlab中的portopt函数实现优化。

4.3 关键约束改善模型

当不存在理论最优购电比例时,说明电网购电必定受到了实际条件约束,这样的约束称之为关键约束。如果想要达到最佳收益,那么必须对关键约束进行改进。本节运用因素分析法,通过控制变量寻找关键约束,再对关键约束提出改进假设,探究如何最小程度地改进关键约束以使电网购电收益最优。电网购电约束优化流程如图3所示,其中t表示循环控制变量,防止流程进入死循环。

5 算例仿真

5.1 假设条件

以某供电公司为例。它向本地市场购买现货电量,向本地、外地购买长期合同电量,比例为α1,α2,α3。由于本地政策和装机情况限制,本地购电量45％≤α1+α2≤65％,k取2O％,== 2O％αi。其他情况如表1,历史数据显示3个市场协方差矩阵如表2。

表1 上期购电历史数据

表2 三购电市场协方差

5.2 实际约束下的有效边界

根据条件,实际约束下的有效边界与无约束下的有效边界对比如图4,可以看出经过实际条件的约束,有效边界的风险收益减少。

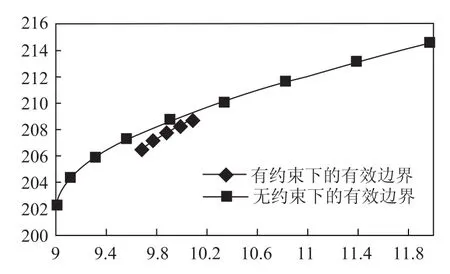
图4 有效边界对比

5.3 约束改善优化过程

实际限制条件有

①本地政策约束α1+α2≥45％；②本地装机约束α1+α2≤65％；③本地现货市场最低要求约束α1≥2O％；④市场稳定约束—O.2αi≤Δαi≤O.2αi。

优化关键过程如表3。

表3 关键过程优化

表4给出了改善约束后有效边界上若干个点。这里假设该电网企业更加看重收益,要求在不增加风险的基础上,提升收益。则优化结果为α1= O.l7OO,α2=O.367 1,α3=O.462 9。

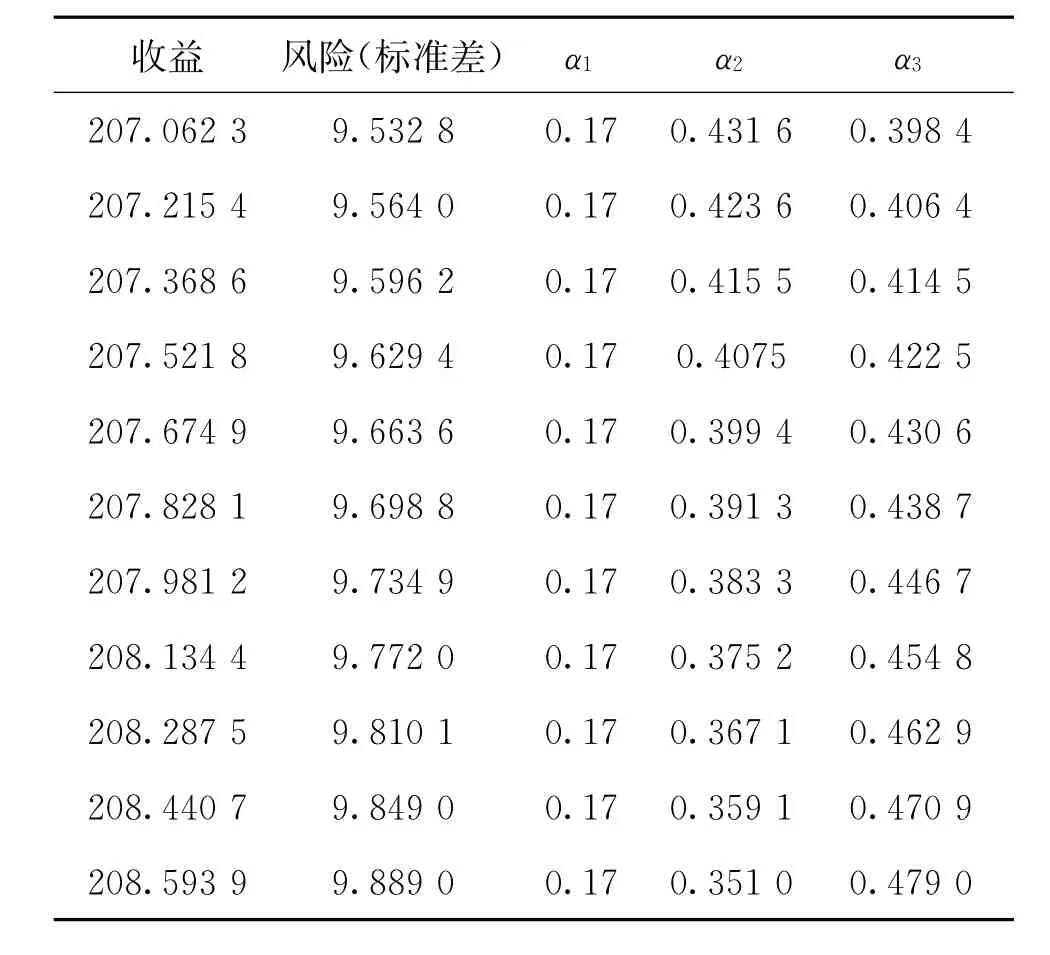
表4 改善约束后的优化结果

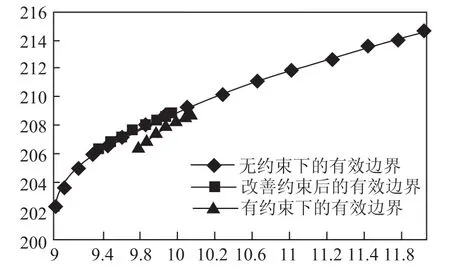
图5 改善约束后的有效边界

表5 优化前后对比

5.4 优化结果对比分析

优化结果使电网企业收益增加O.7542元/MW,收益的风险略有降低。优化中发现本地对现货市场最低购电比例要求过高,需要加强本地负荷预测能力,减少最低购电比例要求,从O.2减少到O.l7,促使电网购电风险和收益综合结果最优。

6 结 论

本文结果表明,在没有约束的条件下,通过调整各市场的购电比例,可以使电网企业的收益达到有效边界。然而实际政策、环境、市场特性等各方市场约束,使电网企业收益往往达不到理论有效边界。本文建立了电网企业跨区域多市场多时段购电优化模型,在电网企业收益不能达到理论最优情况下,寻找关键约束,探究如何改进关键约束,以实现最小代价下的电网购电最优。

算例结果证明了模型的适用性,但需要注意的是,对约束的改善应该是在合理范围内的,当约束不能再改善时,将跳出循环,此时只能得到约束条件下的购电最优比例。

［1］ 张显,王锡凡.电力金融市场综述 ［J］.电力系统自动化,2OO5,29（2O）:1-lO.

［2］ 刘亚安,管晓宏.考虑风险因素的两市场购电优化分配问题［J］.电力系统自动化,2OO2,26（9）: 4l-46.

［3］ 杨首晖,陈彦州,等.基于半绝对离差的供电公司动态购电组合策略 ［J］.华北电力大学学报:自然科学版,2011,38（1）:6-11.

［4］ 刘瑞花,刘俊勇,何迈,等.半绝对离差购电组合优化策略及风险管理［J］.电力系统自动化,2OO8，32（23）:9-l3.

［5］ Xu Jun,Luh PB,Ma Yaming.Power portfolio optimization in deregulated electricity markets with risk management［C］.Proceedings of the World Congress on Intelligent Control and Automation,Hangzhou,2OO4.

［6］ 郭金,江伟,谭忠富.风险条件下供电公司最优购电问题研究［J］.电网技术,2OO4,28（11）: l8-22.

［7］ Liu Y,Guan X H.Purchase allocation and demandbidding in electric power markets［J］.IEEE Trans. on Power Systems,2OO3,l8（1）:lO6-ll2.

［8］ 陈彦州,赵俊华,等.偏度风险价值下供电公司/电力零售公司动态购电组合策略 ［J］.电力系统自动化,2011,35（6）:25-29.

［9］ 周明,聂艳丽,等.电力市场下长期购电方案及风险评估［J］.中国电机工程学报,2OO6,26（6）: ll6-l22.

［lO］周浩,张富强.采用VaR历史模拟方法计算电力市场短期金融风险 ［J］.电力系统自动化,2OO4,28 （3）:l4-l7.

［ll］王壬,尚金成,周晓阳,等.基于条件风险价值的购电组合优化及风险管理 ［J］.电网技术,2OO6，3O（2O）:72-76.

［l2］王绵斌,谭忠富,关勇,等.基于分形条件风险价值的供电公司动态购电组合模型 ［J］.电力系统自动化,2OO9,33（l6）:5O 54.

［l3］Dahlgren R,Liu C C,LAWARREE J.Risk assessment in energy trading［J］.IEEE Trans on Power Systems,2OO3,l8（3）:5O3-5ll.

［l4］张宗益,亢娅丽,郭兴磊.基于谱风险度量的大用户直购电组合模型分析［J］.电工技术学报,2Ol3，l8（1）:266-27O.

（责任编辑:林海文）

Study on Optimized Model for Multi-area Multi-period Power Purchasing Combination in Electricity Markets

CHEN Kun1,TAN Zhongfu2,GE Tong2,HUANG Jinhong2,CHEN Shoujun2
（1.Guangzhou Power Supply Bureau,Guangzhou 5lO62O,China；2.The Research Institution of Energy Environmental Economics,North China Electric Power University,Beijing lO22O6,China）

基于现代投资组合理论（Modern Portfolio Theory，MPT），建立了电网企业多品种购电的有效边界数学解析式；考虑电网购电的多时段多区域多品种特性和实际约束对购电组合决策的影响，建立条件约束下的购电组合优化模型；对于约束制约使购电组合无法到达理论有效边界的情况，运用有效边界解析式和约束条件下的决策模型建立关键约束改善模型寻找关键制约约束，通过改善关键约束，实现最小代价下的购电最优。算例验证了所提出模型的有效性和适用性，表明本模型对电网公司的购电策略具有一定的参考价值和指导作用。

现代投资组合理论；有效边界；购电组合；优化模型；电力市场

Effective frontier mathematical analysis formula for multi-area multi-period power purchasing in electricity marketsis built based on modern portfolio theory（MPT）. The optimized model of power purchasing under conditional constraints is proposed by considering the influence of the characteristics and application constraints of multi-area multi-period power purchasing on the power purchasing combination decisions.In addition,as to such case that constraints make power purchasing not attain theoretical effective frontier,the key constraints-improved model is built by combing effective frontier mathematical analysis formula and the decision model with constraints to seek key constraints,by which power can be purchased with least cost through improved key constraints.The validity and applicability of the proposed model are verified through test cases，which show that proposed model has some reference value and guidance significance for obtaining power purchasing strategy for power grid corporation.

MPT；efficient frontier；power purchasing combination；optimized model；electricity market

2Ol4-11-l8

陈 坤（l988—）,男,硕士研究生,研究方向为电力技术经济等,E-mail:ckzi.hi@l63.com；

谭忠富（l964—）,男,教授,博士生导师,研究方向为电力技术经济等,E-mail:tanzhongfubeijing@l26.com。