基于累积自学习机制的驾驶员路径选择博弈模型

贺 琳，周代平

（1.重庆交通大学 交通运输学院，重庆 400074；2.深圳市新城市规划建筑设计有限公司 城市交通所，广东 深圳 518100）

基于累积自学习机制的驾驶员路径选择博弈模型

贺 琳1，周代平2

（1.重庆交通大学 交通运输学院，重庆 400074；2.深圳市新城市规划建筑设计有限公司 城市交通所，广东 深圳 518100）

为弥补已有驾驶员路径选择博弈模型将驾驶员视为完全理性的不足，探求无诱导信息情况下路网交通流临界状态，将驾驶员视为有限理性，其依赖累积时间感受收益做出下一次的路径选择策略，并以驾驶员的行程时间感受作为决策收益建立了基于累积自学习机制的无诱导信息驾驶员路径选择博弈模型。利用该模型，分析了驾驶员路径选择行为对路网交通流的影响，并通过仿真验证得出了不同初始状态下的模型博弈平衡结果。仿真结果表明：博弈平衡状态与路网车流总量及初始流量分配比例密切相关。当路网车流总量小于或接近路网总通行能力时，不发布诱导信息，路网的交通流分布达到稳定平衡，路网通行能力利用率较高；当路网车流总量远大于路网总通行能力时，不发布诱导信息，路网交通流分布会形成峰谷平衡，不能有效利用路网通行能力，应采取相应的交通管理措施。

交通诱导；累积自学习机制；模糊博弈；驾驶员路径选择；有限理性

0 引言

进入21世纪后，我国经济的高速发展带动了汽车行业的快速发展，人均汽车拥有量的增长速度相当惊人，道路建设土地面积的不足与汽车拥有量飞速增长之间的矛盾日益突出。随着路网系统的完善，交通压力逐渐增大，交通诱导开始引起人们的注意。由于诱导信息是建议性的，当诱导信息发布以后，驾驶员是否接受诱导信息、是否会形成拥堵漂移以及是否有必要发布诱导信息等都是管理者所需要考虑的问题。另一方面，在实际交通网络中，大部分路网并没有交通诱导系统，因此有必要分析在无诱导信息条件下路网交通流的分布平衡，用以指导该路网系统是否有必要发布诱导信息。由此可知，对驾驶员路径选择行为的研究是分析解决路网交通压力逐渐增大问题的关键。

针对驾驶员路径选择问题，国内外学者开展了相关研究。李振龙[1]建立了驾驶员在诱导信息下的路径选择模型；鲁丛林[2]运用Stackberg博弈建立了无诱导信息条件下的驾驶员反应行为博弈模型和完全信息条件下驾驶员反应行为博弈模型，并得出了相同的路况条件下，不同性质的诱导信息对路网交通流的分布影响不同的结论。但是，以上博弈模型都是将驾驶员视作完全理性的，这与现实情况略有出入。Katsikopoulos K.V.等[3]发现在路径选择的实验中，如果一组出行时间的平均值低于某一参照出行时间，出行者表现为“风险规避”；而当平均值高于某一参照出行时间时，则表现为“风险追求”；曾松等[4]提出了驾驶员的某条路径期望行程时间源于驾驶员的驾驶经验；赵凛等[5]建立了基于前景理论的先验信息下路径选择理论模型，指出了驾驶员的驾驶经验能有效影响驾驶员的路径选择。Roth A.E.等[6]、Erev I.等[7]认为出行者进行路径选择的同时也是在不断地实践，通过多次不同的选择，出行者会总结出几次选择的路径中最佳的路径，并将其作为自己今后选择路径的依据，所以路径的选择也是一个学习的过程，进而转化成自身的经验。故在实际出行中，驾驶员不是完全理性的，对驾驶员路径选择影响最大的是近期经验。

本文认为自学习机制的“近期经验”参考的不仅是驾驶员的上一次出行的路径选择，而是考虑驾驶员前k次的时间感受经验对其第k+1次的路径选择的影响，故将每位驾驶员每次路径选择的时间感受进行累积，驾驶员依赖累积的时间感受收益做出下一次的路径选择策略，即：“累积自学习机制”。本文以模糊数学为工具，建立基于有限理性累积自学习机制的博弈模型，并给出模型的求解算法，最后对仿真结果进行分析讨论。

1 累积自学习机制

交通出行是一个多人参与的复杂社会活动，出行选择必然受到多方面的影响。首先，虽然驾驶员在出行前追求的是自身利益的最大化，但是其在做出路径选择策略时会受到其他驾驶员决策的影响，即驾驶员之间存在博弈的关系[8]。其次，受驾驶员自身的局限性限制（如信息了解不全面、判断不准确等），驾驶员并不是完全理性地做出决策，故应将驾驶员看作是有限理性的决策者。最后，驾驶员每次出行所对应的交通状况不是固定不变的，驾驶员要在一次次的出行中学习和调整策略，从而达到自己的出行期望，故应将驾驶员的出行过程看作是一个学习过程来讨论。综上所述，驾驶员的出行路径选择过程应作为一个有限理性博弈过程来研究。

以往的研究包括最优反应动态模型[9]、复制者动态模型[10]和虚拟行动模型[14]这三大有限理性博弈中经典的学习模型，要求局中人对其他博弈方的决策策略有一定的了解。然而在驾驶员的实际出行选择中，驾驶员很难了解到其他大部分出行者的路径选择策略，故有学者提出驾驶员的策略选择更多地取决于自身的近期经验[7]。

因此，本文以在出行之前驾驶员对行程时间有一个模糊的预期为基础，认为博弈的演化过程中局中人是一种“自我学习”，提出了自学习机制：若驾驶员第k次选择的路径行程时间能达到模糊预期，即驾驶员对第k次决策的收益感到满意，则驾驶员第k+1次将会继续选择该路径；若驾驶员在第k次选择的路径行程时间未能达到模糊预期，则驾驶员第k+1次就有可能改变决策，选择其他路径。在自学习机制的基础上，考虑驾驶员决策收益的累积效应，提出累积自学习机制，即驾驶员将过去的各决策收益进行累积，借以判断选择出最佳决策。

2 模型建立

2.1 模型假设

出行时间的长短是影响路径选择最重要的标准[11]，美国联邦总局（BPR）提出路段行程时间函数的公式为[12]：

式中：T为自由行驶时（交通量为0）的路段行程时间（h）；c为路段通行能力（pcu/h）；q为路段实际交通量（pcu/h）；∂,γ为模型待定参数，一般取∂=0.15,γ=4。

本文以驾驶员的实际行驶时间作为驾驶员选择某条路径所获得的收益。考虑如图1所示的简单路网，A到B地有L1与L2两条路径，L1与L2的道路通行能力分别为c1与c2,q1,k与q2,k为驾驶员第k次通过L1与L2的实际交通量，t1,k与t2,k为车辆第k次通过L1与L2到达B地的实际通行时间，t0为驾驶员从A地开往B地的期望时间。

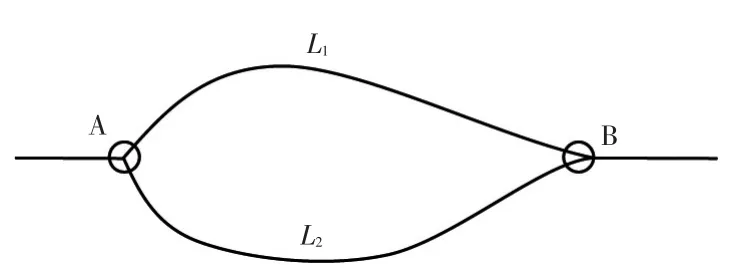
图1 路网示意图

将路径L1与L2座位化处理：座位化处理作为一种虚拟处理手段，没有长度之分，为了记录每位驾驶员每次选择了哪条路径，同时保证每个驾驶员都能记录到，故将两条路径都虚拟成具有Q个座位的路径，如图2所示。

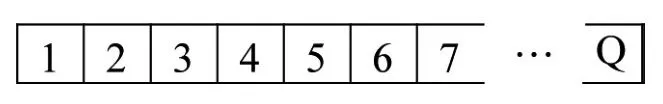
图2 路径L1、L2的座位化处理

设每次参与博弈的局中人总数一定（等于Q），给参与博弈的每位驾驶员依次编上从1到Q的号码，且驾驶员的编号保持不变。

设LN1p,i与LN2p,i分别表示路径L1与L2第i次博弈第p个座位的状态，若LN1p,i=1,LN2p,i=1，则表示路径L1与L2第i次博弈第p个座位有人；若LN1p,i=0,LN2p,i=0，则表示路径L1与L2第i次博弈第p个座位为空。因此，若第p位驾驶员在第i次博弈选择路径L1，则：LN1p,i=1,LN2p,i=0；反之，若第p位驾驶员在第i次博弈选择路径L2，则：LN1p,i=0,LN2p,i=1。所以第i次博弈路径L1与L2的流量为：

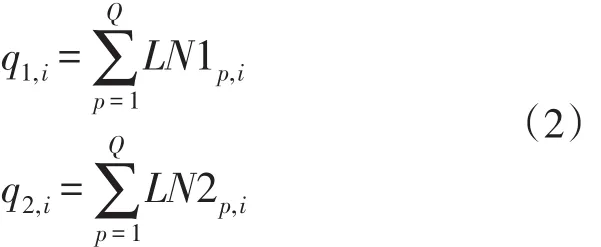
2.2 满意度隶属函数

满意度是指驾驶员对从A地开往B地所花实际时间的满意程度，它是个模糊的概念。隶属函数是模糊数学的一种理论，它的作用是将模糊信息定量化。故用隶属度函数来确定驾驶员满意度，其取值本身也反映了从A地开往B地所花实际时间对驾驶员满意度的隶属程度。取论域，模糊集A1,A2,A3分别表示“满意”、“一般”、“差”，则它们的隶属函数分别为[13]：

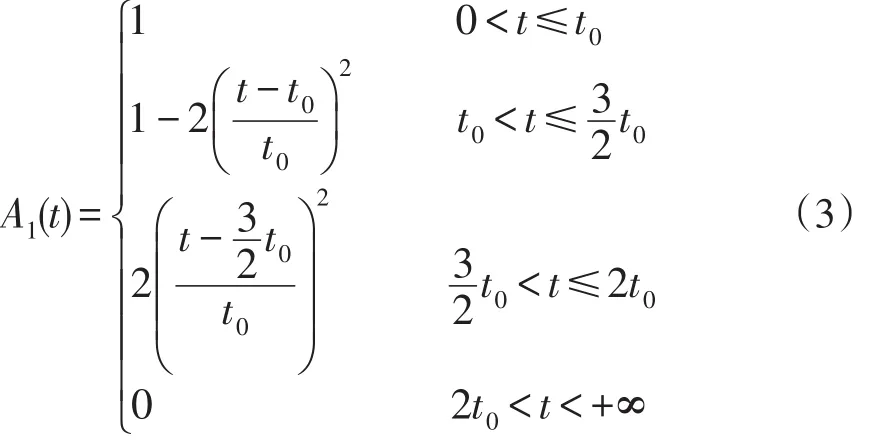
若Max(A1(t),A2(t),A3(t))=A1(t)，则t∈A1，驾驶员对实际驾驶时间t感觉“满意”；若Max (A1(t),A2(t),A3(t))=A2(t)，则t∈A2，驾驶员对实际驾驶时间t感觉“一般”，若Max(A1(t),A2(t),A3(t))=A3(t)，则t∈A3，驾驶员对实际驾驶时间t感觉“差”。

建立路径L1和L2的时间感受收益函数E1(t1)与E2(t2)：

式中：t1,t2为路径L1和L2上的驾驶员时间感受。

2.3 无诱导信息累积自学习机制

无诱导信息条件下的累积自学习机制是指：在有限理性自学习机制下，第p位驾驶员第k+1次的车辆路径选择策略取决其前k次某条路径选择所获得的累积收益。具体表达如下：

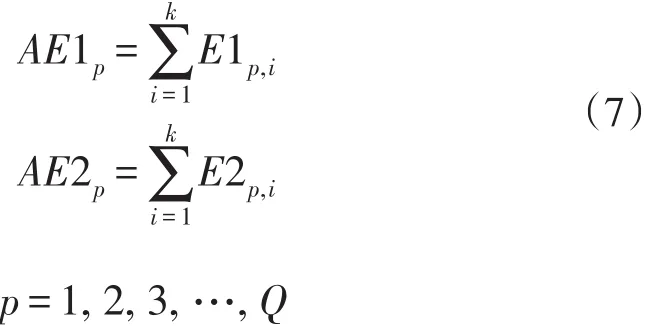
式中：AE1p为第p位驾驶员前k次路径选择中，选择路径L1的累积时间感受收益；AE2p为第p位驾驶员前k次路径选择中，选择路径L2的累积时间感受收益；E1p,i为第p位驾驶员第i次选择路径L1的驾驶员时间感受收益；E2p,i为第p位驾驶员第i次选择路径L2的驾驶员时间感受收益；Q为参与博弈的总车辆数（设每次参与博弈车辆总数不变）。若第p位驾驶员第i次选择路径L1，则：E1p,i=E1(t1),E2p,i=0；若第p位驾驶员第i次选择路径L2，则：E1p,i=0,E2p,i=E2(t2)。

在无诱导信息累积自学习机制中，第p位驾驶员的第i+1次路径选择策略取决于其自身的累积时间感受收益AE1p和AE2p。驾驶员通过对自身经验的累积与学习，判断选择出“有限理性的最优方案”，借以得出第i+1次的路径选择方案，即若AE1p＞AE2p，则第i+1次选择路径L1；若AE1p＜AE2p，则第i+1次选择路径L2；若AE1p=AE2p，则驾驶员的第i+1次路径选择以行为强化理论为依据，通过第i次的路径选择收益来决定第i+1的路径选择方案。也就是，当驾驶员对第i次的路径选择收益满意时，则其第i+1次的选择将与第i次保持相同；而当驾驶员对第i次的路径选择收益的满意度为差时，则其第i+1次将会选择其他路径；当驾驶员对第i次的路径选择收益的满意度为一般时，则第i+1次驾驶员将会有β的概率选择其他路径。该模型的战略表达式如下：

（1）局中人：

（2）局中人的策略集：

（3）局中人的收益函数：

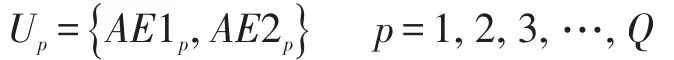
3 模型求解算法

为了求解模型的博弈平衡结果，本文设计了基于累积自学习机制无诱导信息条件下的仿真实验，仿真对象为图1所示的简单路网，并以路径L1上的流量反映模型的博弈平衡结果。具体算法如下：

Step1：初始化模型，给c1,c2(c1＞c2)，T,β赋值（定值），给m,Q赋上初始值m=0.1（m为路径L1的初始分配比例），Q=1000，座位化路径L1,L2，确定路径L1,L2的初始交通量q1(1)=round (mQ),q2(1)=Q-q1(1)，将q1(1)名驾驶员随机坐到路径L1的座位上，将q2(1)名驾驶员随机坐到对应L1上空位置的L2的座位上，最后找出初始时每位驾驶员路径选择方案；

Step2：i=1，统计第i次路径L1和L2的交通量，计算第i次路径L1和L2的时间感受E1p,i,E2p,i，并统计前i次的累积时间感受收益AE1p和AE2p；

Step3：判断AE1p和AE2p大小，确定驾驶员的第i+1次路径选择方案；

Step4：若i＞100，则转Step5，否则i=i+1，转Step2；

Step5：若m＞1，则转Step6，否则m=m+ 0.1，转Step1；

4 具体算例

为了验证基于累积自学习机制无诱导信息模型的博弈结果能否达到平衡，本文对该模型进行了仿真验证。在模型验证中，局中人总数Q，即参与博弈的车辆的初始值为1 000辆；道路L1的通行能力c1=1500pcu/h，道路L2的通行能力c2=1000pcu/h；自由行驶时（交通量为0）的路段行程时间T=30min；满意度为一般时驾驶员变换路径选择的概率β=0.25[14]；局中人总数的增加步长Δq= 500pcu/h；重复博弈的次数k=100。仿真结果如图3所示。

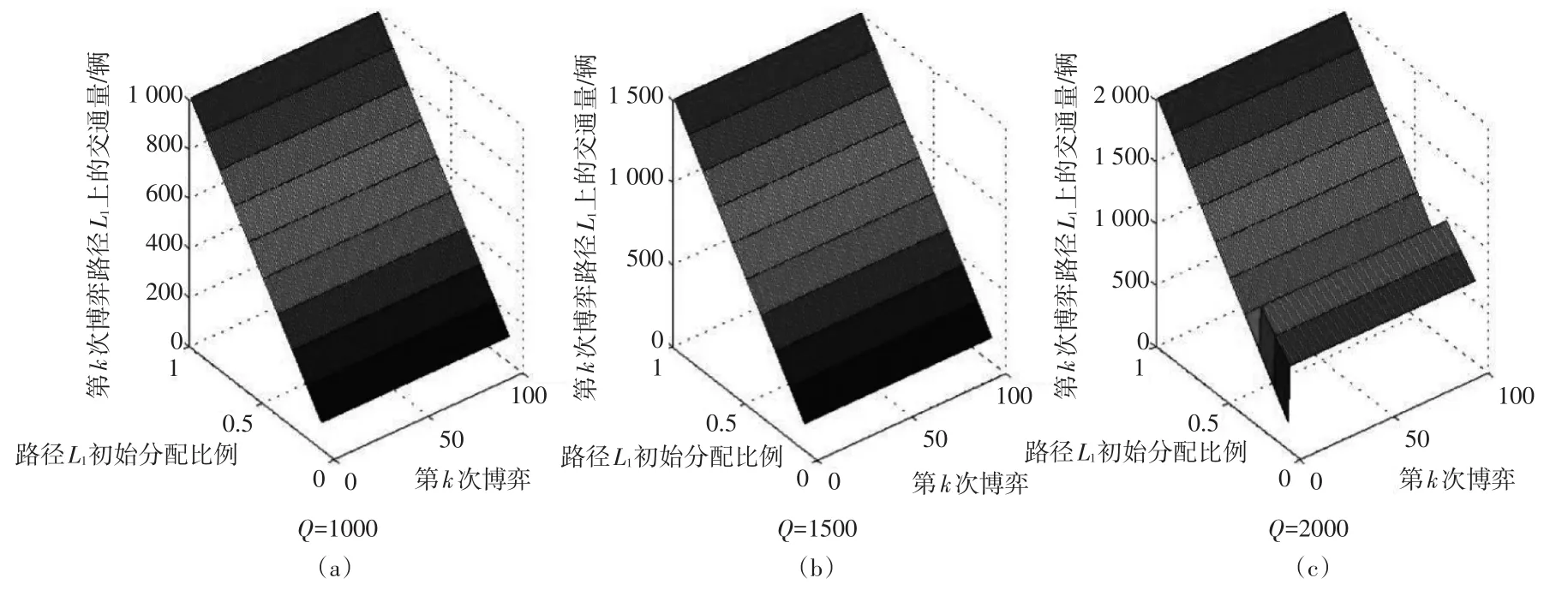
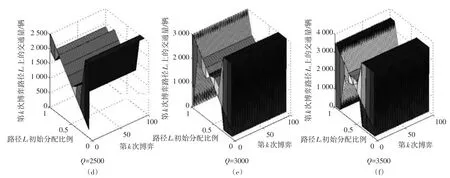
图3 第k次博弈路径L1上的流量

由图3可知，在局中人总数Q和路径L1的初始分配比例m一定时，经过多次重复博弈，路径L1上的流量总为1个定值或为某2个值，即在累积自学习机制下，无诱导信息博弈模型最终会达到平衡。若路径L1上的流量在博弈达到平衡时总为1个定值，则其博弈结果状态为稳定平衡，若路径L1上的流量在博弈达到平衡时为某2个值交替出现，则其博弈结果状态为交替平衡或峰谷平衡。图3的仿真结果显示，随着参与博弈的车辆总数增加，博弈结果的平衡状态由稳定平衡逐渐转变成了交替平衡和峰谷平衡。为进一步分析模型的仿真结果，本文在进行足够多次博弈后（以保证博弈达到平衡），抽取了不同的局中人总数Q下，随着m的变化第99次和第100次的仿真结果（见图4、图5）。

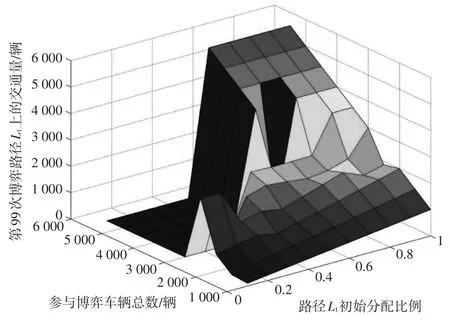
图4 无诱导信息下累积自学习机制第99次博弈结果

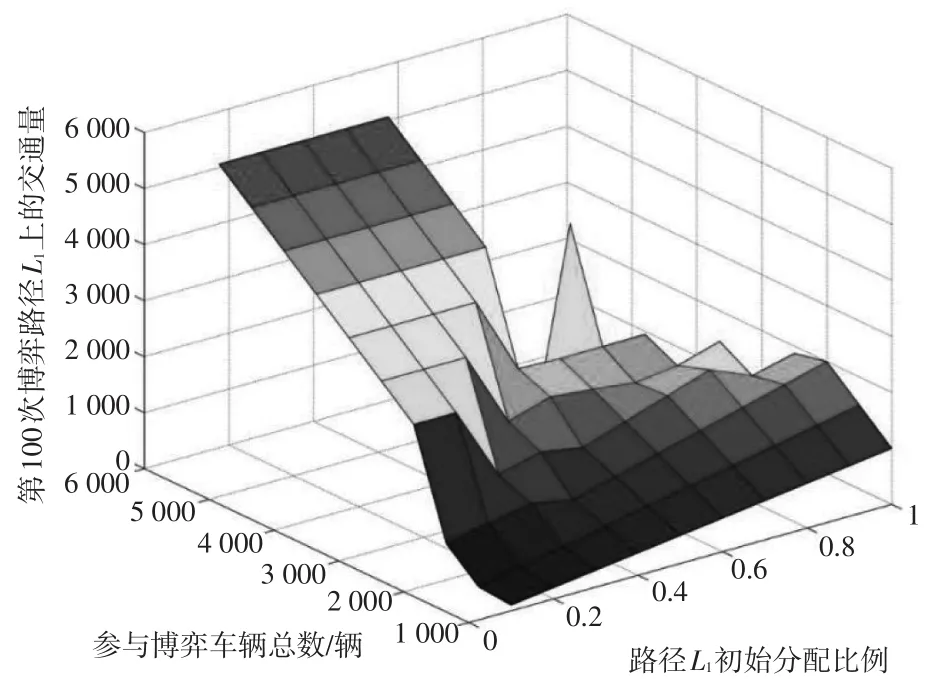
图5 无诱导信息下累积自学习机制第100次博弈结果

对比图4和图5可知：当Q小于路网总通行能力2 500pcu/h时，第100次的博弈结果和第99次的博弈结果相同，当Q大于路网总通行能力2 500pcu/h时，第100次的博弈结果和第99次的博弈结果具有显著差异，当Q保持一定时，博弈结果会随L1的初始分配比例变化而变化。故当路网车流总量远小于路网总通行能力时，路径L1的初始流量所占比例m对路网博弈平衡状态无显著影响，博弈平衡状态为稳定平衡；当路网车流总量接近路网总通行能力时，路网博弈平衡状态与m相关，博弈状态会呈现稳定平衡或交替平衡；当路网车流总量超过路网总通行能力时，博弈平衡状态呈现峰谷平衡。

仿真结果表明，基于累积自学习机制无诱导信息模型的博弈结果最终会达到平衡，且博弈结果的平衡状态与Q,m相关。当路网车流总量小于或接近路网总通行能力时，若不发布诱导信息，路径L1,L2的拥挤度接近，对路网通行能力具有较高的利用率；当路网车流总量远大于路网总通行能力时，若不发布诱导信息，路网系统会形成峰谷平衡，路径L1,L2的拥挤度出现“两极化”现象，对路网总通行能力的利用率较低，此时应采取相应的交通管理措施，提高路网通行能力的利用率。

5 结语

本文讨论了基于累积自学习机制的无诱导信息车辆路径选择问题，建立了以驾驶员累积时间感受为收益函数的博弈模型，并通过仿真得出了模型的博弈平衡结果。仿真结果表明，在有些初始情形下，不发布诱导信息，路网的交通流分布也能达到稳定平衡，并且对路网通行能力具有较高的利用率；在路网总流量远大于路网总通行能力或其他特殊初始情形下，不发布诱导信息，路网交通流分布呈现峰谷平衡，不能有效利用整个路网系统，应采取相应的交通管理措施，如发布诱导信息。

本文只研究了不发布诱导信息下的博弈平衡结果，今后的研究可以讨论在发布诱导信息条件下的博弈平衡结果，借以对比得到在各种初始情形下发布诱导信息是否能有效提高路网总通行能力的利用率，是否有必要发布诱导信息等相关结论，为交通诱导决策提供依据。

[1]李振龙.诱导条件下驾驶员路径选择行为的演化博弈分析[J].交通运输系统工程与信息，2003，3（2）：23-27.

[2]鲁丛林.诱导条件下的驾驶员反应行为的博弈模型[J].交通运输系统工程与信息，2005，5（1）：58-61.

[3]KATSIKOPOULOS K V,DUSE-ANTHONY Y,FISHER D L,et al.Risk Attitude Reversals in Driver's Route Choice When Range of Travel Time is Provided[J].Human Factors, 2002,44(3):466-473.

[4]曾松，史春华，杨晓光.基于实验分析的驾驶员路线选择模式研究[J].公路交通科技，2002，19（4）：84-88.

[5]赵凛，张星臣.基于“前景理论”的先验信息下出行者路径选择模型[J].交通运输系统工程与信息，2006，2（6）：42-46.

[6]ROTH A E,EREV I.Learning in Extensive-Form Games: Experimental Data and Simple Dynamic Models in the In⁃termediate Term[J].Games and Economic Behavior,1995 (8):164-212.

[7]EREV I,BEREBY-MEYER Y,ROTH A E,The Effect of Adding a Constant to All Payoffs:Experimental Investiga⁃tion and Implications for Reinforcement Learning Models [J].Journal of Economic Behavior and Organization,1999, 39(1):111-128.

[8]刘建美.诱导条件下的路径选择行为及协调方法研究[D].天津：天津大学，2010.

[9]谢识予.经济博弈论[M].2版.上海：复旦大学出版社，2002.

[10]王济川，郭丽芳.抑制效益型团队合作中“搭便车”现象研究——基于演化博弈的复制者动态模型[J].科技管理研究，2013，12（21）：191-195.

[11]OUTRAM V E,THOMPSON E.Driver Route Choice[C]// Proceedings of PTRC Annual Meeting.London:PTRC An⁃nual Meeting,1977:39-53.

[12]杨佩坤，钱林波.交通分配中路段行程时间函数研究[J].同济大学学报：自然科学版，1994（1）：27-32.

[13]杨纶标，高英仪，凌卫新.模糊数学原理及应用[M].广州：华南理工大学出版社，2011：1-67.

[14]周元峰.基于信息的驾驶员路径选择行为及动态诱导模型研究[D].北京：北京交通大学，2007.

Game Theory Model of Driver's Route Selection Based on Cumulative Self-Learning Mechanism

HE Lin1,ZHOU Dai-ping2
(1.School of Traffic&Transportation,Chongqing Jiaotong University,Chongqing 400074,China; 2.Shenzhen New Land Tool Consultants Pte.,Ltd.,Urban Traffic Brunch,Shenzhen 518100,China)

In order to make up the shortage of regarding the drivers as totally rational by the existing game theory models of driver's route selection,and search the fettle of network traffic flow without induc⁃ing information,the drivers'rationality was deemed bounded,so he or she made the selection decision of next path according to the cumulative feeling gains of time.The driver's feeling of travel time was consid⁃ered as the gains of decision,then the model of the driver's routing selection without inducing informa⁃tion was established based on cumulative self-learning mechanism,and the impact of the driver's route choice behavior on road network traffic flow was analyzed.Finally the equilibrium results of fuzzy game on different initial states were obtained by the simulation.The simulation results show that the balance of fuzzy game is closely related to the total amount of road network traffic and initiatory flow distributionratio.When the total amount of road network traffic is less than or close to the capacity of network,the distribution of network traffic flow reaches a stable equilibrium and the utilization rate of the capacity of network is higher without inducing information.When the total amount of road network traffic is over the capacity of network,the distribution of network traffic flow forms a peak balance,the capacity of network can't be used effectively,and appropriate traffic management measures should be taken.

traffic guidance;cumulative self-learning mechanism;fuzzy game;drivers'route selec⁃tion;bounded rationality

U491.13

：A

：2095-9931（2015）04-0049-07

10.16503/j.cnki.2095-9931.2015.04.008

2015-04-18

贺琳（1991—），女，四川广安人，硕士研究生，研究方向为交通规划。E-mail：helin19911127@163.com。