基于改进遗传算法的车辆路径问题

甘 宝，薛玉玺，魏文萍

（兰州交通大学 交通运输学院，甘肃 兰州 730070）

基于改进遗传算法的车辆路径问题

甘 宝，薛玉玺，魏文萍

（兰州交通大学 交通运输学院，甘肃 兰州 730070）

为了研究物流中心的服务效率和车辆的合理调度方案，以汽车载重量作为影响车辆路线安排的主要因素，以经典的车载容量约束条件下的车辆路径问题为原型建立数学模型，通过求解该数学模型的最优解来获得车辆最优路径。由初始状态随机生成的可行解作为初始的车辆路径方案，通过改进的遗传算法不断地调整染色体的交叉和变异概率进行优化，最终得到物流中心车辆安排的合理方案。通过多次求解算例，都能够得到满意的车辆路径方案，不仅验证了该数学模型的有效性和实践性，而且也验证了改进后遗传算法的收敛性和鲁棒性，同时得到了改进遗传算法交叉和变异概率的调整范围。该模型和算法不仅可以提高物流中心的服务效率，而且可以为物流中心的车辆调度方案提供支持和帮助。

物流配送；车辆路径问题；遗传算法；交叉算子；收敛性

0 引言

当代物流业在电子商务的推动下蓬勃发展，客户对货物配送的要求也越来越高。就配送中心而言，要考虑如何降低配送费用、缩短配送时间以及提高配送效率和服务水平等。要实现这些目标，车辆路径安排（又称车辆路径问题，Vehicle Routing Problem，简称VRP）是关键所在。该问题由Dantzig和Ramse[1]于1959年首先提出，其一般定义为：对一系列装、卸点，合理组织行车路线，使车辆有序地通过它们，在满足一定的约束条件（如：货物需求量、车辆容量限制、行驶里程限制、时间限制等）下，达到一定的目标（如：费用最少、时间最短、用车数最少等）。车辆路径问题是一个NP（Non-Deterministic Polynomi⁃al，非确定性多项式）完全问题[2]，只有在节点较少时能够求得精确解。因此，关于车辆路径问题的各种算法的研究成为热点，尤其是启发式算法，如由Clarke和Wright[3]提出的节约法、Gillett和Miller[4]提出的扫描法、Fisher和Jaikumar[5]建立的一般分配算法以及Pureza和Franca[6]研究的Tabu搜索算法等。这些算法[7]用以求解车辆路径问题时都很有效，但也有各自的局限：如节约法按节约量从大到小构造路径，具有运算速度快的优点，但存在未组合点零乱、边缘点难于组合的问题；而扫描法却不是渐进优化算法[7]。如何针对车辆路径问题的特点，构造运算简单、寻优性能优异的启发式算法，不仅对于配送系统而且对于许多可转化为车辆路径问题的优化组合问题具有十分重要的意义。

遗传算法（Genetic Algorithm，简称GA）是John H.Holland[8]根据生物进化模型提出的一种优化算法。它是一种以自然选择和遗传理论为基础，将生物进化过程中适者生存的规则与种群中染色体的随机信息变化机制相结合的全局寻优搜索算法[8]。遗传算法通过构造特征问题的解，形成初始种群，然后通过反复的选择、交叉、变异算子的作用进行迭代，求得问题的满意解或最优解。该算法具有隐含并行操作机制，针对编码而非针对问题本身进行操作，寻优规则由概率决定，快速收敛等特点，因此发展很快，在很多领域有着广泛的应用[9]。为此，本文在GA基础上构造初始可行解，并设计算法来求解车辆路径问题。

1 VRP数学模型

假定配送中心用K辆车对N个需求点进行配送，每辆车的载重量均为C，每个需求点的需求量为Di(i=1,2,…,n)，需求点i到需求点j的距离为dij，配送中心的编号为0。

此外，还包括以下约束和假设：

（1）所有客户只能被1辆车访问，并且只能被访问1次；

（2）所有车辆必须由配送中心出发并最终回到配送中心；

（3）所有车辆必须满足容量限制，不可超载；

（4）假设车型相同，容量相同；

（5）假设配送中心唯一。

为建模方便，再引入2个决策变量：和。其中，当车辆k由客户i到客户j时，取，否则；当车辆k访问客户i时，取，否则。

由此，建立车辆路径问题的数学模型如下：

在模型中，式（1）为目标函数，要求配送完所有需求点的总路径最短；式（2）保证每辆车仅访问1个需求点；式（3）保证每个需求点仅被1辆车访问；式（4）表示共有K辆车从配送中心出发；式（5）为容量约束。

2 VRP的遗传算法

遗传算法是一种基于生物自然选择和基因遗传学原理的优化搜索方法。自然选择学说是进化论的核心思想，根据进化论，生物的发展进化主要有三个原因：遗传、变异和选择[10]。

遗传是指子代总是与亲代具有相似性，通过遗传，亲代将自身的某些特质、性状遗传给后代，被称为生物进化的基础。变异是指子代和亲代出现不相似的现象，即子代永远不会和亲代一模一样。它是生物个体之间相互区别的基础。变异为生物进化和发展创造了条件。选择是指生物群体所具有的精选能力，决定着生物进化方向[11]。自然选择是指生物在自然界的生存环境中适者生存，不适者被淘汰的现象。生物就是在遗传、变异和选择三种因素的综合作用下，不断适应环境、进化和发展的。

进化论的自然选择过程蕴含着一种搜索和优化的先进思想。遗传算法正是吸取了生物系统“适者生存，优胜劣汰”的进化原理，从而使它能够提供一个在复杂空间里进行的“鲁棒性”搜索算法。

2.1 算法编码

针对车辆路径问题解的特点，本文采用占焱发[12]提出的自然数编码方式进行染色体编码，即一条染色体便是一个配送方案，染色体长度为N+K+1，n为客户数量，K为车辆数，其编码形式如下：，其中的一条子路径用表示，含义是：第k辆车从配送中心出发，配送完相应的需求点后返回配送中心；0代表配送中心；表示第k辆车访问的第i个客户。

2.2 初始种群的产生

随机产生互不相同的N个数（范围为1～N），在这组数的前后两端各加一个0，然后从第1个0元素之后开始，计算需求点对应的累计需求量，如果，则在第i个需求点之后加入0元素，至此前两个0元素之间的需求点由车辆1来配送；以此类推，直到加入第K个0元素为止；第K个0元素与末端的0元素之间的需求点由第K辆车来配送。这样做可以保证所产生的初始解满足车辆的容量约束、每个需求点只能被1辆车访问以及每辆车只能访问1个需求点的约束条件。重复上述步骤n次，就可以产生n个初始可行解。本文为保证种群的多样性和快速求解，取n=500，即产生500个初始种群。

2.3 适应值函数

适应值函数是评价每个染色体优劣的函数，一般与问题的目标函数有密切关系，染色体的适应值函数（简称适值）是染色体优劣的量化指标。VRP的目标是使车辆的总里程最短，其目标函数如式（6）所示，本文将其目标函数直接作为适应值函数。

式中：f为适应值函数；表示第i辆车由需求点j到k的行驶距离（为简单起见，这里采用两点之间的直线距离），对于不满足容量约束的染色体由于不能求得其目标函数，所以令其适应值为一个很大的正整数，即f=max。

2.4 评价函数与种群选择

评价函数（记为Eval(V)）是遗传过程中优胜劣汰的基本依据[10]。利用评价函数选择染色体的一般原则是优良的染色体以一个较大的概率被选择而得以进入种群，反之劣质的染色体被选中的概率较小。

本文采用基于序的评价函数，首先将群体按适应值排序，之后依据下式进行选择：

式中：n为种群大小；fi为染色体i的适应值。

评价函数可以作为种群中染色体被选入种群的概率。利用评价函数可以确定染色体进入种群的累计概率：

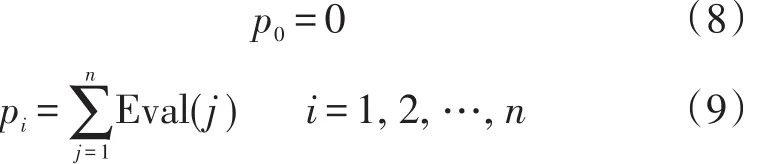
式中：pi为第i个种群的累计概率，当pi-1＜r≤pi时，第i个染色体进入种群（r为伪随机数）。

在此，将评价函数值的全体称为“轮盘赌”。本文采用轮盘赌的方式选择种群。

2.5 交叉算子

交叉操作用于组合出新的个体，并使算法能够搜索更多的解，同时降低对有效模式的破坏概率。由于车辆路径问题编码的特殊性，为了防止交叉后出现不满足车辆容量限制的现象以及两个0元素相邻的现象，本文采用双亲双子法进行单点交叉运算，取交叉概率Pc=0.95。随机选取一位基因进行交换，不能为0元素，并且两个父代染色体的基因不能相同。为了保证解的合法性，必须要做内部交换，防止1个需求点被多次访问以及两个0元素相邻的现象。例如：

式中：Pa和Pb分别为两个父代染色体，随机选取交叉位9，分别对应染色体Pa和Pb中的基因7和 3，将Pa中的7与Pb中的3互换，得到；检查染色体中的基因，将其中重复的元素换成缺失的元素，得到两个子代。

2.6 变异算子

当交叉操作产生的后代适配值不再进化且没有达到最优时，就意味着算法的早熟收敛，而变异则是增加染色体多样性的一个手段，它可以得到一些新的基因，通常赋予每1个染色体1个相对较小的变异概率。本文采用互换变异算子，由于是单点操作，所以变异概率取值稍大，取Pm=0.3。互换变异即随机交换染色体中两个不同基因的位置，为保证染色体的合法性，随机选取两个不同的子路径中不为0的基因进行交换。如某个体为[012｜3045067｜80]（其中“｜”表示变异位），分别选取子路径[01230]中的2和子路径[06780]中的7进行互换变异，得到新个体为[017304506280]。

2.7 算法终止条件

虽然遗传算法在理论上具有以概率1收敛的极限性质，但在实际中很难实现，因此在求解实际问题时追求的是快速搜索到具有一定质量的满意解。常用的终止规则有：给定最大遗传迭代步数，给定最佳搜索解的最大滞留步数，给定问题的下界和1个偏差度，当前最优解与下界的差不大于偏差度时停止运算。本文在给定最大遗传迭代步数达到2 000次时，终止算法。

2.8 算法流程

基于改进遗传算法的车辆路径问题算法流程如图1所示，具体分为以下几个步骤：

Step1：产生500个初始可行解作为初始种群，并令k=1，转Step2；

Step2：利用评价函数评价第k代种群P(k)，并对种群按适应值由小到大进行排序，转Step3；

Step3：保存到目前为止的最优解及其适应值，转Step4；

Step4：如果k≤2000，转 Step5；否则转Step8；

Step5：依据轮盘赌从父代中获取种群，转Step6；

Step6：对由Step5产生的种群进行交叉操作，转Step7；

Step7：对由Step6产生的种群进行变异操作，转Step2；

Step8：获取最优方案并输出结果，算法结束。

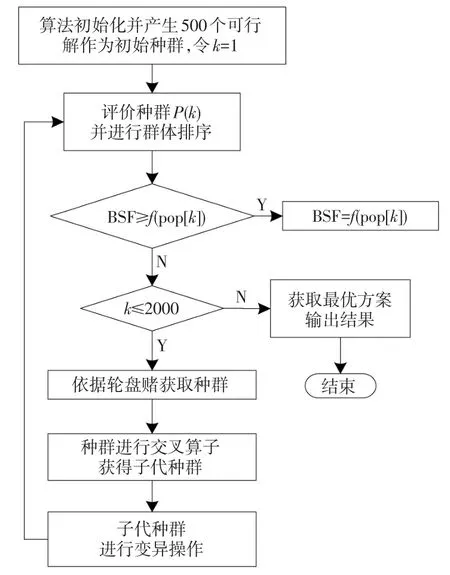
图1 算法流程图

3 实例分析

某配送中心地理坐标为（40，50），向100个需求点配送货物，每辆车的载重为200，现有货车10辆，每个需求点的地理坐标和货物需求量如表1所示（其中，NO为需求点编号，X为横坐标，Y为纵坐标，D为需求点的需求量）。下面在保证每个需求点的送货量和车辆不超载的前提下，求出配送中心对这100个需求点送货的最短路径。

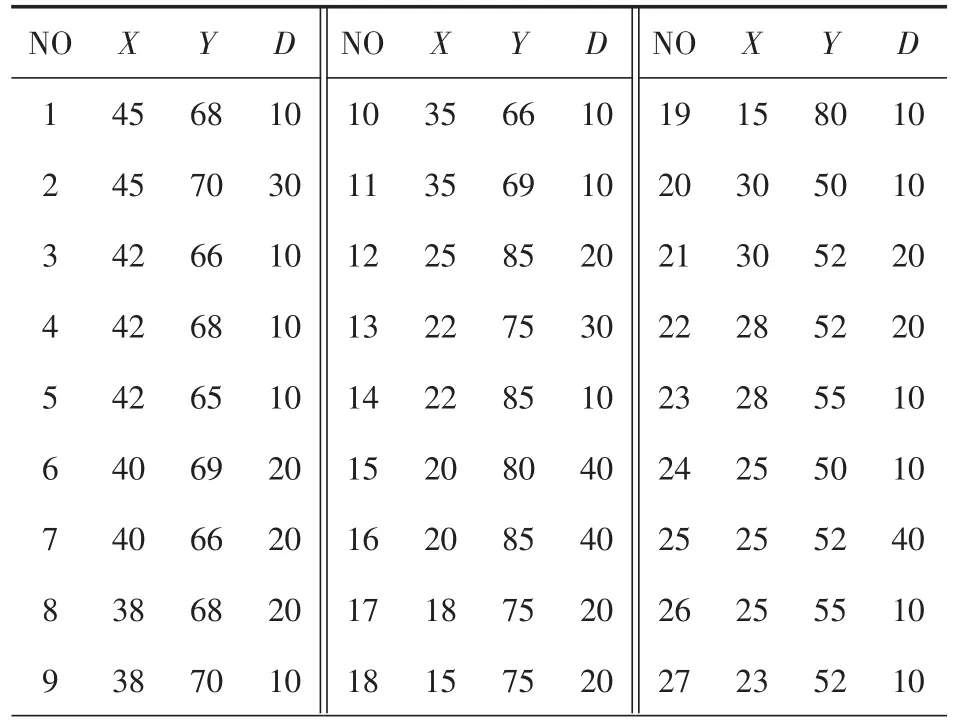
表1 需求点地理坐标及需求量一览表

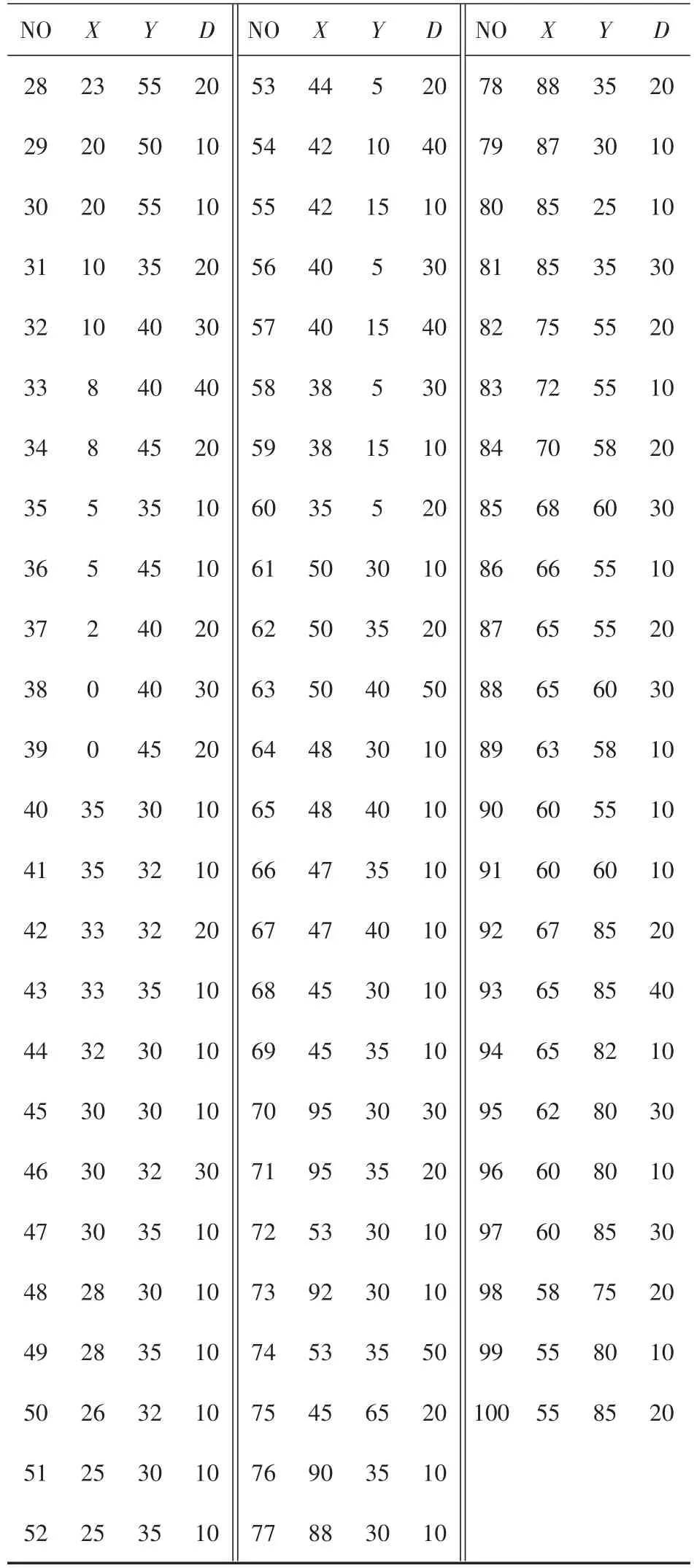
表1 （续）

用C++语言、CodeBlock开发工具编写遗传算法，在CPU主频为2.53GHz、内存为4G的电脑上对该算法进行实例验证，求得了当前最优解。将当前最优解的迭代过程以图的形式展示如下：第1代、第500代、第1 000代、第2 000代的车辆路径分别如图2、图3、图4、图5所示（横、纵坐标表示客户点的地理位置）。当前最优解的适应值函数f与进化迭代次数N的曲线关系如图6所示。

图2 第1代的车辆路径图

图3 第500代的车辆路径图

图4 第1 000代的车辆路径图

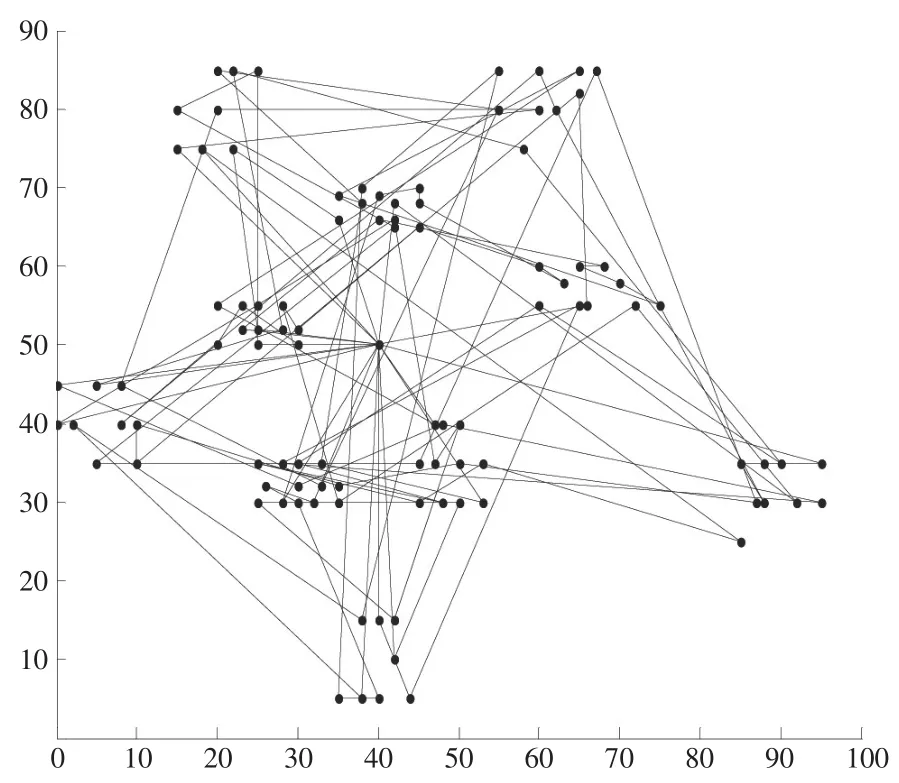
图5 第2 000代的车辆路径图

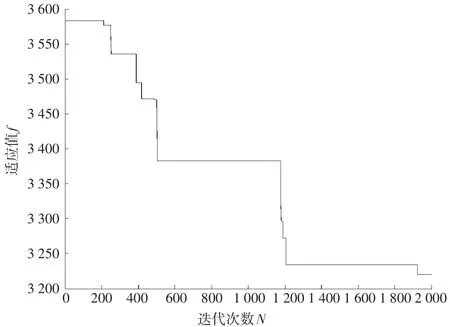
图6 当前最优解适应值f与迭代次数N的关系图

在第1代中，即初始可行解中，车辆路径如表2所示，总的车辆里程为3 583.64。

表2 GA第1代时的车辆及其服务对象

在第2 000代中，即最优解中，车辆路径如表3所示，求得总的车辆里程为3 220.07。

表3 GA第2000代时的车辆及其服务对象

相比之下，最优解比初始解节约里程约363.57。由于初始种群数量很多，所以初始解中的最优解与当前最优解的差距相对就小。上述图表形象地说明了本文设计的遗传算法在求解VRP时的收敛情况及其鲁棒性。

4 结论

本文通过车载容量约束的车辆路径问题的模型以及改进的遗传算法研究了物流中心的配送路径优化问题，得出以下结论。

（1）初始种群规模影响着算法收敛速度，规模越大，染色体就越具有多样性，算法收敛也就越快。

（2）交叉概率与变异概率的取值对优化结果有着直接的影响：当交叉概率Pc取0.9～1时，本文算法可以有效地求出当前最优解；生物进化中变异只起辅助作用，但本文中变异算子与交叉算子同等重要，因此变异算子的概率取值偏大，取Pm≥0.3。

（3）对于受车载容量约束的车辆路径问题，本文设计的遗传算法能够很好地求得其满意解，可以为现实中物流配送方案提供支持和帮助。

不过，本文的研究还存在以下不足之处：没有考虑服务时间窗的约束；没有考虑车载容量可以允许轻微超载；在算法设计方面比较单一，应该考虑多种智能算法的混合运用，这样可以提高求解速度和最优解的质量。以上这些都是未来进一步研究的方向。

[1]史春燕，黄辉.车辆路径问题：研究综述及展望[J].物流科技，2014（12）：75-77.

[2]陶波，朱玉琴.改进的动态规划法在车辆最短路径问题中的应用[J].重庆工学院学报：自然科版，2009（1）：24-27.

[3]CLARKE G,WRIGHT J W.Scheduling of Vehicles from a Central Depot to a Number of Delivery Points[J].Operations Research,1964,12(4):568-581.

[4]GILLETT B E,MILLER L R.A Heuristic Algorithm for the Vehicle Dispatch Problem[J].Operations Research,1974 (22):340-349.

[5]FISHER M L,JAIKUMAR R J.Ageneralized Assignment Heuristic for Vehicle Routing[J].Networks,1981(11):109-124.

[6]PUREZA V M,FRANCA P M.Vehicle Routing Problems via Tabu Search Metaheuristic[R].Montreal,Canada:Cen⁃tre for Research on Transportation,1991.

[7]程世东，刘小明，王兆赓.物流配送车辆调度研究的回顾与展望[J].交通运输工程与信息报，2004（3）：93-97，116.

[8]姜大立，杨西龙，杜文，等.车辆路径问题的遗传算法研究[J].系统工程理论与实践，1999（6）：41.

[9]常洪江.遗传算法综述[J].电脑学习，2010（3）：115.

[10]贺国先.现代物流系统仿真[M].北京：中国铁道出版社，2008：198.

[11]祁振华.基于敏捷制造的动态联盟组建过程中伙伴选择问题的研究[D].沈阳：沈阳工业大学，2005.

[12]占焱发.基于遗传算法的物流配送车辆路径问题研究[D].西安：长安大学，2010.

An Improved GeneticAlgorithm for Vehicle Routing Problem

GAN Bao,XUE Yu-xi,WEI Wen-ping
(School of Traffic and Transportation,Lanzhou Jiaotong University,Lanzhou 730070,China)

In order to research the service efficiency and reasonable scheduling scheme of vehicles of a logistics center,the vehicle load was taken as the main factor which influenced the vehicle routing ar⁃rangement,the classical capacitated vehicle routing problem was used as the prototype to establish the mathematical model,and the optimal path was obtained by solving the optimal solution of the mathemati⁃cal model.The initial feasible solution generated randomly served as the initial vehicle routing plan,a reasonable vehicle arrangement plan of logistics center was found finally by constantly adjusting chromo⁃somal crossover and mutation probability of the improved genetic algorithm to optimize the solution.It verifies the effectiveness and practicality of the proposed model,the convergence and robustness of the improved genetic algorithm by solving a numerical example for many times.Meanwhile the adjusting range of crossover and mutation probability of the improved genetic algorithm are obtained.The model and algorithm not only improves the service efficiency of logistics center,but also provide support and help for the vehicle scheduling scheme of logistics center.

logistics distribution;vehicle routing problem;genetic algorithm;crossover operator; convergence

U492.312

：A

：2095-9931（2015）04-0088-07

10.16503/j.cnki.2095-9931.2015.04.013

2015-07-06

甘宝（1989—）男，甘肃泾川人，硕士研究生，研究方向为交通运输规划与管理。E-mail:ganbao2012@163.com。