拉力型岩土预应力锚界面粘结劣化研究进展

张思峰，李琳，李英勇

（1.山东建筑大学交通工程学院，山东济南250101；2.山东省交通运输厅公路局，山东 济南250002）

0 引言

岩土预应力锚固结构由于其对岩土体扰动较小、施工快、经济、安全等优点逐渐成为高陡边坡、大坝、深基坑等大型岩土加固工程中的首选方法，并取得了显著的经济和社会效益。按其内锚固段受力形式来说，拉力型岩土预应力锚固结构是当前应用范围最广、使用数量最多的一种锚固结构形式。如长江三峡水利枢纽工程中，在长为1621 m的船闸边坡上，采用了4000余根长度为21～61 m、拉力值为3000 kN的预应力锚索及近10万根长度为8～14 m的高强度锚杆进行加固，其中绝大部分为拉力型岩土预应力锚固结构。

拉力型岩土预应力锚固结构是指通过杆体与注浆体以及注浆体与周围岩土体之间的粘结应力来提供张拉力的预应力结构，其特点是荷载施加后在其内锚固段前部出现高度应力集中现象，且随张拉力逐级增大剪应力峰值逐渐内移，界面粘结逐渐劣化，存在渐进破坏的可能［1－2］。室内试验与现场调研表明，大量预应力锚固结构失效都是由于界面粘结劣化造成的，因此，这种在外荷载作用下的界面渐进粘结劣化是决定拉力型岩土预应力锚固结构内锚固段长期耐久性的关键因素。界面粘结劣化的研究对实际工程中内锚固段合理长度及其使用寿命的确定等具有重要理论指导意义。文章通过对国内外在拉力型岩土预应力锚固结构内锚固段界面粘结应力及粘结劣化理论研究、试验研究及数值模拟研究等方面的现状回顾，阐述了拉力型岩土预应力锚固结构界面粘结劣化三个主要研究方面的现状，提出了拉力型岩土预应力锚固结构界面性能研究中存在的问题及发展方向。

1 界面粘结应力及粘结劣化的理论研究

1.1 界面粘结应力（或剪应力）的理论研究

最初的界面作用机理认为在锚固结构各界面上不存在粘结劣化或者滑移现象，杆体、注浆体及围岩体三者之间协调变形。基于此假设，Li等提出了指数形式分布的界面剪应力分布公式［3］；Wei等提出了内锚固段轴向力分布的两参数复合幂函数模型［4］。在国内，曹国金等根据Mindlin问题的位移解，推导了拉力型预应力锚杆的杆体轴力及界面剪应力沿杆体分布的弹性理论解，分析了拉力型锚杆的受力分布特征，提出了确定拉力型锚杆支护长度的方法，对锚杆在不同岩体中的有效锚固长度进行了计算，并分析了影响锚杆有效锚固长度的各种因素［5］。洪海春等基于弹性理论，将锚杆作用力假定为在半空间体边界上受到的法向集中力，研究了拉力型预应力锚固结构内锚固段界面剪应力沿长度方向的分布规律，发现内锚固段最大剪应力并非出现在中点上，而是位于接近内锚固段前端的一侧，且内锚固段剪应力的分布为单峰曲线，其两端为零（或近似为零）、中间某处为最大值，通过引入相关参数估算极限承载力，研究了锚固段长度的取值问题［6］。蒋忠信认为拉力型锚索、锚杆锚固段的剪应力是非均布的，剪应力分布曲线是以0为渐近线的单峰曲线，通过对不同工程中实测的锚杆、锚索数据进行拟合，发现适宜采用三参数高斯曲线来描绘杆体内锚固段界面剪应力的分布模式，并推导得出了曲线的拐点、极大值、积分及平峰比等特征值［7］。宗全兵等基于Winkler假设的局部变形理论，将预应力锚索受力段分为一系列的子锚固段，研究了非均质地层中预应力锚索的受力特征，得出了杆体轴向力及界面剪应力的理论解［8］。钟志彬等根据锚杆的实际工作状态，在对全长粘结锚杆受力特性采取一定假设的基础上，分析了岩体与杆体之间的相互作用机理；考虑锚杆轴向力的分布并结合荷载传递分析方法和弹性力学Kelvin问题解，得出了剪应力沿锚杆长度分布的计算公式。他认为在弹性状态下，锚杆剪应力从外锚头处的零开始迅速增大，达到最大值后沿锚杆长度方向呈指数形式衰减，经过一定长度后，剪应力又趋近于零，即杆体剪应力的作用范围仅分布在锚头附近很有限的范围内［9］。李冲等根据锚杆—围岩相互作用原理，建立了全长锚固拉力型预应力锚杆杆体受力计算模型，并结合现场实测等方法分析了杆体轴力、剪应力与预张力的关系以及杆体轴力与剪应力的分布规律，认为锚杆杆体轴向应力、界面剪应力与围岩条件、锚杆自身性质以及施加预应力的大小等有关［10］。上述研究对弹性状态下岩土预应力锚固结构内锚固段杆体轴力及各界面剪应力分布规律进行了理论分析，推导了界面剪应力分布的一般规律，即表现为以0为渐近线的峰值靠近内锚固段前端的单峰曲线，相关研究成果对界面粘结应力分布特征的确定起到了积极的推动作用，也为拉力型岩土预应力锚固结构内锚固段合理长度的设计奠定了理论基础。

1.2 界面粘结劣化的理论研究

后来人们发现随轴向荷载的逐级增大存在界面粘结的劣化现象，即界面剪应力峰值点不断向杆体深部转移，且伴随着界面之间的相对滑动。对此特征，Benmokrane采用三阶段线性函数来描述接触面上剪应力与剪切位移的关系：第一阶段为共同变形阶段，接触面呈现弹性无损状态；第二阶段为接触面的劣化损伤阶段，剪应力随剪切位移的增长而相应降低；第三阶段接触面完全处于损伤阶段，只有摩擦力存在［11］。Ana等和Yazici等分别采用两段式线性及四段式（其中三段用于描述粘结劣化段）复合曲线模型来描述上述关系［12－13］。Yazici等将注浆体的破坏过程分为三个阶段：弹性阶段、部分开裂阶段和完全开裂阶段，并分别对各个阶段的力学特性进行了分析［14］。Shuqi等还根据拉拔试验，建立了考虑残余剪应力的粘结—滑移模型，得出了界面剪切应力和轴向荷载的分布规律［15］。以上研究成果将界面粘结劣化过程进行了分阶段描述，并分析了各阶段的界面力学特性，一定程度上揭示了内锚固段各界面在外荷载作用下的粘结滑移特性，但上述分析大都是根据拉拔试验得到的粘结应力与滑移量之间的L—S曲线得到，并不能从本质上反映其内部变化机理，因此所采用的界面粘结裂化关系曲线也就有所不同。

在国内，对于拉力型岩土预应力锚固结构界面粘结劣化或滑移特性的理论研究还处于起步阶段。张季如等假定锚固体与周围岩土体之间的剪应力随剪切位移呈线性增加，以此建立了描述杆体荷载传递机理的双曲函数模型，获得了锚杆摩阻力（即界面剪应力）和剪切位移沿杆体长度方向的分布规律，并结合埋设于黏性土中4根灌浆锚杆的现场拉拔试验成果，分析了杆体荷载的传递特性：锚杆摩阻力由内锚固段顶端向尾端衰减，呈现不均匀分布，峰值出现在顶端；随荷载递增，峰值摩阻力将从内锚固段顶端向末端迁移，而后又随着拉拔力的增加重驻内锚固段顶端［16］。邹金锋等基于损伤理论，定义了岩土体剪切损伤变量及其相应的损伤演化方程，依据岩土体在锚杆侧向剪应力作用下发生的损伤特性和锚杆在岩土体中的荷载传递机理，建立了锚杆在岩土体损伤时的荷载传递微分方程并推导出考虑岩土体损伤情况下的锚杆轴力、剪切位移和侧摩阻力沿锚杆长度分布的解析解，该理论解考虑了锚杆长度、锚杆直径和岩土体的损伤特性、剪切模量及压缩模量等因素的影响［17］。徐波等首先依据Mindlin位移解推出了锚杆剪应力沿长度方向的分布函数，并以此建立了锚杆荷载传递的微分方程，根据方程进一步推导了杆体位移沿深度方向的分布函数［18］。谷拴成等认为混凝土中锚杆的荷载传递特性主要取决于螺纹钢筋—混凝土界面的剪切特性，他基于锚杆滑移所产生的剪胀效应及破坏机制，建立了适用于混凝土中螺纹锚杆的荷载传递模型，并得到了塑性破坏条件下杆体轴力和剪应力的解析解，探讨了锚杆轴力和界面剪应力沿锚固长度方向随相对剪切位移的分布规律，分析了不同拉拔力、锚杆直径、剪胀角等因素对荷载传递的影响规律［19］。叶根飞通过总结已有的内锚固段各界面剪切滑移本构模型，并基于Benmokrane建立的界面滑移本构模型，应用荷载传递函数法，建立了弹塑性理论空间模型，得出了杆体界面上剪应力沿长度方向分布的理论解，同时结合现场试验得到的杆体荷载—位移曲线将界面粘结劣化过程分为弹性变形、滑移变形、脱粘出现与发展及完全脱粘四个阶段，不同阶段的界面上具有不同的界面剪应力分布规律［20］。尤春安等基于预应力锚索锚固体从岩土体中拔出计算模式，通过分析锚固体与灌浆材料的界面层变形—破坏过程，建立了内锚固段的剪滞—脱黏模型，同时将内锚固段分为弹性区、塑性滑移区和脱黏区，采用与Coulomb条件关连的流动法则导出了界面应力分布的理论解，并认为锚固体承受荷载的主要工况是塑性滑移状态，在研究或进行锚固体设计时应主要基于这种变形状态［21］。可以看出，目前国内学者对荷载逐级增大情况下岩土预应力锚固结构内锚固段各界面的粘结裂化性能开展了卓有成效的理论研究工作，也取得了较多丰硕成果，但从理论上分析界面粘结裂化后剪应力峰值内移规律的相关研究还很少见。

从上述分析可以看出，研究者们对预应力锚固结构内锚固段的粘结劣化特性开展了针对性的理论研究工作，使人们对粘结劣化的认识从最初的感性认知提高到科学的理性分析，但从粘结劣化的细观机理出发分析和解释粘结劣化现象仍是当前研究的难点和重点。在此方面，李新平等根据复合材料力学的理论和方法，将岩土预应力锚固系统看作一种由岩体（基体材料）、锚杆（增强材料）和砂浆（黏结材料）构成的复合加固材料，建立了该复合加固材料的细观力学等效模型，推导了其弹性常数的计算公式，并定量分析了岩体强度、锚杆尺寸及布置、砂浆强度等因素对锚固复合支护系统力学性能的影响，还理论分析了预应力锚固复合材料的宏观力学性能与各组分材料的力学性能及细观结构之间的相关关系［22］。尤春安等在进行预应力锚索内锚固段界面力学特性试验研究的基础上，探讨了锚固体界面在荷载作用下的变形规律及失效条件，并基于此建立了有骨料的灌浆材料界面细观力学模型，从细观层面上对预应力锚索内锚固段从弹性变形到塑性滑移以致脱黏失效的全过程进行了研究，提出了锚固体拉拔失效的几个阶段：弹性变形阶段、塑性滑移阶段及脱黏变形阶段［23］。

在界面粘结劣化的机理研究方面，Windsor认为粘结劣化是由于组成界面应力的三种分力：粘结力、机械咬合力及表面摩擦力依次消失或减弱的结果，而接触面上只有残余应力存在［24］。朱焕春等和蒋良潍等认为当已破坏锚固段内的残余应力及未破坏段提供的粘结力足以平衡外荷载时，杆体将重新处于无滑移的共同变形状态［25－26］。上述关于粘结劣化机理的研究提升了人们对拉力型岩土预应力锚固结构荷载传递机理的科学认知，但要真正掌握粘结劣化现象的本质还有赖于更深入的细观机理研究。

2 拉力型岩土预应力锚固结构界面粘结劣化的试验及数值模拟研究

2.1 界面粘结劣化的试验研究

拉力型岩土预应力锚固结构的界面粘结劣化现象最初是由室内试验和现场试验发现的。Stillborg早在1984年就发现在非粘性土中随着外荷载增大，存在界面粘结应力峰值点向内锚固段远端转移的现象［27］。其后，许多学者各自通过试验验证了类似现象［11－12，28］。而国内对此问题的研究要明显晚于国外，张永兴等设计了6种不同配合比的注浆体，将普通锚、压花锚锚固于硬岩中，通过抗拔试验获得了岩锚的荷载—位移全过程曲线，分析发现普通拉力型锚索在达到极限承载力后持荷能力下降，位移不断增长，分析认为是由于脱黏段转移到内锚固段底部后持荷能力只由摩擦力和机械咬合力共同承担的结果［29］。汪海滨等通过现场预应力岩锚原位拉拔试验发现当内锚固段长度大于一定值后，其长度再增加无助于提高极限抗拔力，且对于内锚固段长度分别为10和12 m的拉力型锚索来说当锚头位移分别达到94.77和128 mm时已无法再承受荷载，索体与注浆体间发生滑移或锚孔内持续带出水泥浆屑［30］。张培胜等也通过室内模型试验发现锚杆承受较小拉力时，杆体滑移量很小，但随着拉力的增加，杆体顶端将会出现较明显的位移，当外荷载达到某一数值后，杆体位移迅速增大，而荷载却无法再继续增加，锚杆失效，由此认为：当杆体所受拉力较小时，锚杆处于弹性工作状态，外荷载主要由杆体外端部的界面粘结力来承担，其曲线的峰值出现在杆体外端；随拉力的增加，杆体外端及其内部剪应力逐步增大；拉力进一步增加后，杆体外端注浆体与杆体之间的界面粘结被破坏，杆体开始产生滑移，外端部剪应力下降，剪应力峰值随之向锚固体深部转移；当拉力增大到一定程度时，内锚固段前端的粘结应力下降至残余应力，由杆体和注浆体之间的摩擦力来抵抗它们之间的相对滑移［31］。韩侃等在一个高速公路边坡预应力锚固工程中，通过对随机抽取的4根预应力锚索进行拉拔试验并比较索体实际伸长量与理论伸长量的差值，发现部分锚索在拉拔过程中出现内锚固段的相对滑移，表现为索体张拉荷载不变的情况下锚头位移随时间而增长，并认为这种锚索荷载的传递和破坏是渐进式的［32］。可以看出，越来越多的室内及现场试验已证明，荷载逐级增大情况下岩土预应力锚固结构内锚固段各界面尤其是杆体－注浆体界面存在渐进粘结裂化现象，即界面剪应力峰值向内锚固段远端逐渐转移，且界面的最终破坏一般呈现出突然性特点。

2.2 界面粘结劣化的数值模拟研究

室内试验和现场试验成果的积累促进了数值模拟计算方法的开展。Serrano等通过数值模拟研究了荷载大小、杆体与浆体、围岩体材料弹性模量比值对粘结应力分布形态的影响［33］。Ana等采用有限差分法分析了冲击荷载作用下预应力锚杆的动力响应，发现自由段长度及预应力大小均对内锚固段的动力性能有较大影响［34－35］。Yiming等采用有限元程序对界面粘结劣化理论模型进行了分析和验证［36］。在国内，任非凡采用Abaqus软件对一种复合锚杆的拉拔试验进行数值模拟，考虑到复合锚杆的破坏形式多为界面破坏，因此作者用改进的Cohesive单元对复合锚杆的4种界面材料进行模拟，数值模拟结果表明钢绞线轴向应力及界面剪应力均服从指数形式分布，且随着荷载的增大，界面剪应力峰值向后转移。复合锚杆的其余界面剪应力同样服从指数形式分布规律，且界面剪应力峰值随主控制面—钢绞线与复合材料界面剪应力峰值的转移而转移［37］。江文武利用三维显式有限差分程序（FLAC3D）建立预应力锚杆拉拔试验数值仿真模型对影响锚杆锚固力的主要影响因素、锚杆拉拔过程中的整体失稳规律等进行了研究，发现锚杆拔出的过程是由慢慢滑移到突然整体失稳的过程，并且锚固体界面剪应力分布规律随锚杆拉拔过程而不断改变，这与汪海滨［30］等和张培胜等［31］所得现场及室内试验结论相同，从而得出拉力型岩土预应力锚固结构在粘结逐渐劣化的过程中变形量很小，而其失稳却是突然性的［38］。张思峰等基于快速拉格朗日分析法，采用FLAC3D软件分析了拉力型岩土预应力单锚体系和群锚体系作用下杆体内锚固段、自由段以及外锚头部位的应力场、位移场及其相应的破坏机理，通过数值模拟发现当内锚固段前部塑性屈服后，后部的压应力集中区呈“锥状”发展，刺入前部拉应力区［39］。上述界面粘结裂化数值模拟方法的开展弥补了理论及试验研究的不足，为进一步揭示界面粘结裂化的机理提供了一定的参考价值，然而，上述基于连续介质力学的数值建模分析方法通常是唯象的，无法从细观本质上把握界面粘结劣化对杆体受力及荷载传递特性的影响，另外，基于连续介质力学的方法在处理粘结劣化这类非连续变形问题时也存在较大局限性。

3 锚固结构界面粘结劣化研究存在的问题

拉力型岩土预应力锚固结构张拉力实际监测结果表明，在预应力锚固结构的整个寿命期内预应力并非是逐级增大或固定不变的，而是由于各种因素影响而处于不断的波动变化之中，呈现出周期性循环荷载的特征（如图1所示），荷载变幅甚至接近杆体锁定荷载的20%［40］。除此之外，在地震力这种偶发的不规则循环荷载作用下，岩土预应力锚固结构的杆体轴力也呈现出循环加载模式，且地震动荷载具有能量大、频率高，受感区域岩土体表现为反复错动或反复拉压运动的特点，这种特殊的循环荷载作用对预应力锚固结构的界面粘结性能也是一个严峻考验［41］。

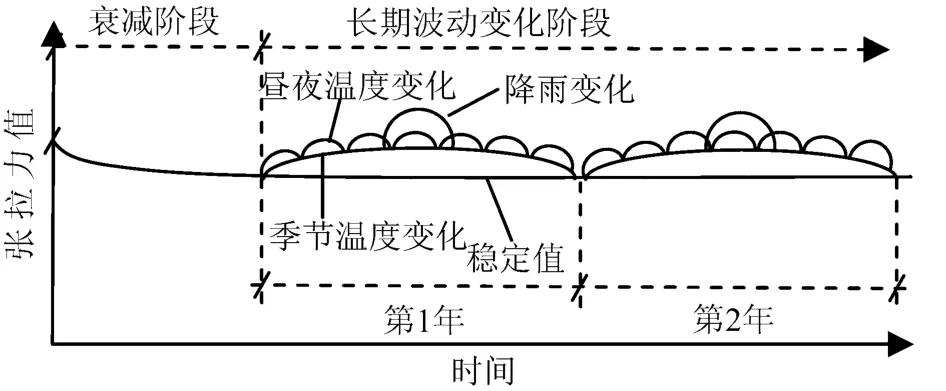
图1 预应力长期变化特征图［40］

对此，李国维等通过现场试验对4 m锚固长度的玻璃纤维增强聚合物（GFRP）锚杆施加非破坏性循环荷载作用，循环次数2次，最大荷载100 kN，并通过锚杆应力计及分布式光纤BOTDR技术测量锚杆杆体应力，监测发现与第1次循环加载相比，相同荷载下第2次循环加载使锚杆杆体相同位置处的轴向应力得到提高，分析认为是由于锚杆与砂浆的耦合程度随循环荷载次数的增加而削弱，结合面强度降低，应力衰减幅度减小，传递深度增加，由此推论，由于环境温度和降水的变化引起的荷载反复会加大锚杆的承载应力［42］。朱焕春等和樊启祥等曾结合三峡船闸闸室高强锚杆进行了三次最大张拉力为600 kN的反复完全加卸载试验［43－44］。试验结果显示不同循环时同一荷载对应的锚杆应力分布有所区别：第1循环时锚杆应力分布正常，前端第1个测点应力最大，应力向深处衰减很快；第2循环时，第1测点应力降低，第2、3测点应力较第1循环显著提高；第3循环时第1、2测点应力降低，更深处的锚杆应力保持增高趋势，这说明循环荷载作用同荷载逐级增大一样将使预应力锚固结构界面产生粘结裂化，从而使锚杆受力深度不断增加。现场试验还发现3个循环后破坏情况基本趋于稳定，但文中所采用的加载方式与工程环境温度、降雨或地震力所形成的荷载变化形式差别较大。张思峰在对某实际边坡加固工程中拉力型岩土预应力锚固结构施工期与长期运营期预张拉力变化特征分析的基础上，提出了预应力锚固结构张拉力变化的大循环及小循环的概念，从而揭示了预张力循环变化的基本特征，以此为基础，通过研制内锚固段疲劳破坏试验装置，在进行室内相似模型试验的基础上，研究了循环荷载作用下内锚固段的长期耐久性问题，发现随荷载变幅的增大，内锚固段所能承受的最终循环次数大致呈指数形式衰减［45］。目前对于因循环加载而引起预应力锚固结构内锚固段粘结劣化现象的研究较少，另外受到试验条件的限制也无法探明粘结劣化过程中锚固体各界面细观组构的演化规律以及各界面两相材料的细观解耦机理，从而也无法从颗粒介质层面揭示荷载作用下界面粘结劣化的细观力学本质及界面裂纹的萌生、分布和发展规律，这无疑限制了对荷载作用下拉力型岩土预应力锚固结构界面粘结劣化机制及界面滑移破坏力学机理、长期耐久性等问题的深入研究。

4 展望

综上所述，目前国内外对于静载作用下拉力型岩土预应力锚固结构界面粘结劣化性能的研究已取得一定成果，但对于动荷载作用下界面粘结劣化的研究较少，在细观层面的精细化分析则更少。针对以上存在的问题，提出如下展望：

（1）界面细观力学行为的物理试验研究是揭示界面粘结劣化机理最直接也是最可靠的方法，但相关研究由于受试验条件限制还很少见。先进的研究方法和技术可被借鉴用来进行岩土锚固结构界面粘结劣化细观机理的相关研究工作。

（2）采用数值模拟软件进行细观数值模拟研究是对界面粘结劣化行为细观物理试验研究的补充和拓展。在此方面以离散元为代表的散体介质数值分析方法由于避免了连续介质本构关系选取这一难题而被逐渐应用于岩土体细观力学性状的研究，为从细观尺度研究宏观问题的内在机理提供了平台，其中尤以颗粒流理论及其PFC程序因其能够模拟固体力学大变形及颗粒介质流动问题而得到了广泛的应用。离散元理论及其相关程序在分析岩土预应力锚固结构界面粘结裂化的发生与发展机制、揭示界面粘结裂化的细观机理方面有其独到的优势。

（3）考虑锚固体长度、循环荷载变幅、应力水平及注浆体强度等因素进行拉力型岩土预应力锚固结构界面粘结劣化的宏观试验研究，从而确定循环荷载作用下以上各因素对界面粘结劣化的影响规律。

［1］曾宪明，林大路，李世民，等.锚固类结构杆体临界锚固长度问题综合研究［J］.岩石力学与工程学报，2009，28：3609－3625.

［2］程良奎，胡建林，张培文.岩土锚固技术新发展［J］.工业建筑，2010，40（1）：98－101.

［3］Li C.，Stillborg B..Analytical models for rock bolts［J］.International Journal of Rock Mechanics and Mining Sciences，1999，36：1013－1029.

［4］Wei J.，Zhou X.W，Zhu Y.A..Combined powermodel for the distribution of axial force in shaft anchor along its length［J］.Journal of China University of Geosciences，2006，17（1）：89－94.

［5］曹国金，姜弘道，熊红梅.一种确定拉力型锚杆支护长度的方法［J］.岩石力学与工程学报，2003，22（7）：1141－1145.

［6］洪海春，胡毅夫，刘志明，等.预应力描索锚固段剪应力分布与锚固段长度研究［J］.岩土力学，2006，27（增）：926－930.

［7］蒋忠信.拉力型锚索锚固段剪应力分布的高斯曲线模式［J］.岩土工程学报，2001，23（6）：696－699.

［8］宗全兵，徐卫亚.基于局部变形理论的非均质地层中预应力锚固受力分析［J］.岩土力学，2009，30（4）：915－920.

［9］钟志彬，吕蕾，邓荣贵.考虑轴力分布的全长粘结锚杆受力分析［J］.防灾减灾工程学报，2013，33（3）：311－315.

［10］李冲，徐金海，李明.全长锚固预应力锚杆杆体受力特征分析［J］.采矿与安全工程学报，2013，30（2）：188－193.

［11］Benmokrane B.， Chennouf A.， Mitri H.S.. Laboratory evaluation of cement-based grouts and grouted rock anchors［J］.International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts，1995，32（7）：633－642.

［12］Yue C.，Tetsuro E.，Yujing J..A rock bolt and rock mass interaction model［J］.International Journal of Rock Mechanics and Mining Sciences，2004，41（7）：1055－1067.

［13］Ana I.，Richard D.N..Modelling of debonding along the fixed anchor length［J］.International Journal of Rock Mechanics and Mining Sciences 2009，46（4）：699－707.

［14］Yazici S.，Kaiser P.K..Bond strength of grouted cable bolts［J］.International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts，1992，29（3）：279－291.

［15］ShuqiM.，Jan N.，Naj A..An analyticalmodel of fully grouted rock bolts subjected to tensile load［J］.Construction and Building Materials，2013，49：519－526.

［16］张季如，唐保付.锚杆荷载传递机理分析的双曲函数模型［J］.岩土工程学报，2002，24（2）：188－192.

［17］邹金锋，李亮，杨小礼，等.基于损伤理论的全长式锚杆荷载传递机理研究［J］.铁道学报，2007，29（6）：84－88.

［18］徐波，吴智敏.混凝土中锚杆荷载传递机理的理论分析［J］.哈尔滨工业大学学报，2008，38（3）：417－422.

［19］谷拴成，崔希鹏.混凝土中锚杆锚固荷载传递特性研究［J］.混凝土，2010，10：27－30.

［20］叶根飞.岩土锚固荷载传递规律与锚固特性试验研究［D］.西安：西安科技大学，2012.

［21］尤春安，战玉宝，刘秋媛，等.预应力锚索锚固段的剪滞—脱黏模型［J］.岩土力学与工程学报，2013，32（4）：800－806.

［22］李新平，王涛，宋桂红，等.锚固层状岩体的复合加固理论与数值模拟试验分析［J］.岩石力学与工程学报，2006，25（2）：3654－3660.

［23］尤春安，战玉宝.预应力锚索锚固段界面滑移的细观力学分析［J］.岩石力学与工程学报，2009，28（10）：1976－1985.

［24］Windsor C.R..Rock reinforcement systems［J］.International Journal of Rock Mechanics and Mining Sciences，1997，34（6）：919－951.

［25］朱焕春，荣冠，肖明，等.张拉荷载下全长粘结锚杆工作机理试验研究［J］.岩石力学与工程学报，2002，21（3）：379－384.

［26］蒋良潍，黄润秋，蒋忠信.考虑孔壁界面滑移－软化的预应力锚索锚固段侧阻力分布［J］.水文地质工程地质，2005，6：61－65.

［27］Stillborg B..Experimental investigation of Steel Cables for Rock Reinforcement in Hard Rock［D］.Sweden：Lulea University of Technology，1984.

［28］Woods R.I.，Barkhordari K..The influence of bond stress distribution on ground anchor design［C］.Ground Anchorages and Anchored Structures.London：Themas Telford House，1997.

［29］张永兴，饶枭宇，唐树名，等.压花锚锚固性能的试验研究与数值分析［J］.岩石力学与工程学报，2008，27（3）：607－614.

［30］汪海滨，高波.预应力锚索荷载分布机理原位试验研究［J］.岩石力学与工程学报，2005，24（12）：2113－2118.

［31］张培胜，阴可.拉力型锚杆锚固段传力机理的全过程分析方法［J］.地下空间与工程学报，2009，5（4）：716－723.

［32］韩侃，李登科，吴冠仲.预应力锚索锚固力拉拔试验分析［J］.岩土工程学报，2011，33（增1）：385－387.

［33］Serrano A.，Olalla C..Tensile resistance of rock anchors［J］.International Journal of Rock Mechanics and Mining Sciences，1999，36：449－474.

［34］Ana Ivanovic，Richard D.Neilson，Albert A.Rodger.Influence of prestress on the dynamic response of ground anchorages［J］.Journal of Geotechnical and Geoenvironmental Engineering，2002，128（3）：237－249.

［35］Ana I.，Andy S.，Richard D.N.，et al.The influence of load on the frequency of rock boltanchorage［J］.Anvances in Engineering Software，2003，34：697－705.

［36］Yiming Z.，Mijia Y..Pull-out behavior of an imperfectly bonded anchor system［J］.International Journal of Rock Mechanics＆Mining Sciences，2011，48：469－475.

［37］任非凡，徐超，谌文武.多界面复合锚杆荷载传递机制的数值模拟［J］.同济大学学报（自然科学版），2011，39（12）：1753－1759.

［38］江文武，徐国元，马长年.FLAC－3D的锚杆拉拔数值模拟试验［J］.哈尔滨工业大学学报，2009，41（10）：129－133.

［39］张思峰，周健，宋修广，等.预应力锚索锚固效应的三维数值模拟及其工程应用研究［J］.地质力学学报，2006，12（2）：166－173.

［40］李英勇，张顶立，张宏博，等.边坡加固中预应力锚索失效机制与失效效应研究［J］.岩土力学，2010，31（1）：144－150.

［41］汪鹏程，朱大勇，徐强.强震作用下加固边坡的动力响应及不同加固方式的比较研究［J］.合肥工业大学学报（自然科学版），2009，32（10）：1501－1504.

［42］李国维，黄志怀，张丹，等.玻璃纤维增强聚合物锚杆承载特征现场试验［J］.岩土力学与工程学报，2006，25（11）：2240－2246.

［43］朱焕春，吴海滨，赵海滨.反复张拉荷载作用下锚杆工作机理试验研究［J］.岩土工程学报，1999，21（6）：662－665.

［44］樊启祥，顾文红.三峡永久船闸高强结构锚杆现场试验研究及质量控制［J］.岩石力学与工程学报，2001，20（5）：657－660.

［45］张思峰.预应力内锚固段作用机理及其耐久性研究［D］.上海：同济大学，2007.