多自由度非线性振动的迭代配点法研究

姜剑，王兆清，庄美玲

（山东建筑大学力学研究所，山东 济南250101）

0 引言

过去几十年，多自由度系统的振动得到了广泛的研究。Moochhala和 Raynor采用近似方法（Approximatemethod）分析了不规则物体的多自由度振动［1］，Huang研究了双自由度非线性系统的谐波振荡［2］，Gilchrist分析了双自由度保守拟线性系统的自由振荡［3］。双自由度系统的振动在物理工程和许多实际工程中都有着非常重要的运用。例如双弹簧支撑的弹性梁、铣床的振动都可以采用双自由度系统振动模型分析研究［4］。双自由度非线性振动系统可归结为两个非线性微分方程，很多情况下，求解非线性方程组的准确解析解是极其困难甚至不可能。因此，求解非线性方程大体上有两类办法，近似解析解法和数值方法。近似解析解法运用最广泛的是摄动方法，该方法不适用于求解强非线性方程并且运用时还有其他很多弱点。许多文献研究了摄动法的改进方法。比如同伦摄动法、max-min approach method［5－6］。Ladygina等 采用多 尺度法（multiscalemethod）分析了双自由度保守系统的非线性振动和它的自振频率［7］。Cveticanin同时采用雅可比椭圆函数和三角函数得到了一个双自由度非线性系统振动的解析解［8－9］。数值方法中，Chen采用广义伽辽金方法分析了双自由度非线性振动问题［10］。Al-Karak运用拉普拉斯分解法求解了非线性微分方程问题［11］。

配点法求解线性微分方程初值问题，可以一次性得到计算节点处的函数值，是一种高效率的计算方法［12］。Rashidinia采用配点法求解了非线性问题［13］。依据未知函数近似方法的不同，配点法主要有基于特征多项式插值的拟谱方法、基于Lagrange插值的微分求积法、基于重心Lagrange插值的重心插值配点法和基于有理Haar函数插值的配点法等［14－17］。拟谱方法是一种高精度数值方法，其具有指数收敛精度［14］。基于重心Lagrange插值的配点法在求解微分方程边值问题和初值问题时，具有很高的计算精度［16，18］。

直接采用配点法离散非线性微分方程，得到非线性代数方程，通常采用Newton法求解非线性代数方程。本文先假设未知函数的初始值，将非线性微分方程组线性化，运用重心有理插值配点法求解线性化的微分方程初值问题，再迭代逼近求解非线性微分方程的数值解。将通过算例详细介绍本文求解多自由度非线性振动方法的高效和高精度性。

1 重心有理插值配点法

1.1 重心有理插值及其微分矩阵

对于给定的插值节点0＝t1＜t2＜… ＜tn＝T和相应的函数值 fj＝f（tj），j＝1，2，…，n，选择任意的整数d满足0≤d≤n，重心有理插值可由式（1）表示为

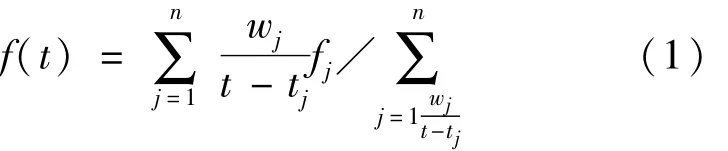
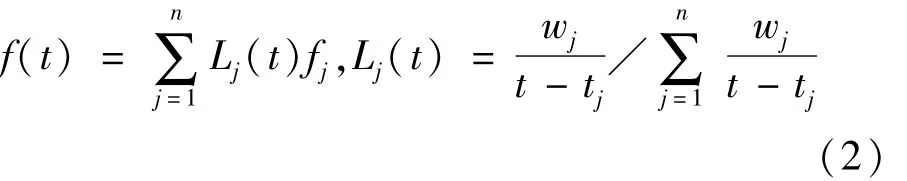
函数f（t）的m阶导数可由式（3）表示为

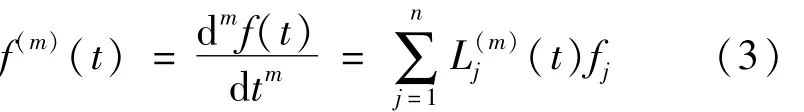
函数f（t）在节点t1，t2，…，tn处的m阶导数可由式（4）表示为

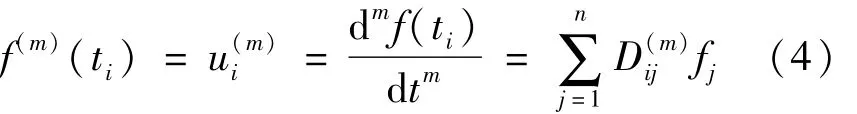
用矩阵的形式（5）表示为

1.2 多自由度系统线性振动控制方程的离散公式

双自由度耦合系统线性振动控制方程一般由式（6）表示为

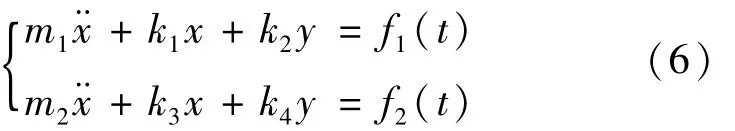
式中：x、y分别为线性系统振动的物理量；t为时间。

将时间区域［0，T］离散为0＝t1＜t2＜… ＜tn＝T，运用重心有理插值近似未知函数可由式（7）得

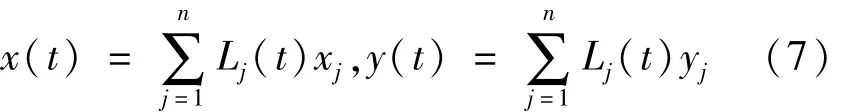
将式代入方程式，利用微分矩阵，并令方程在离散时间点 t1，t2，…，tn上成立，方程式用矩阵的形式（8）表示为

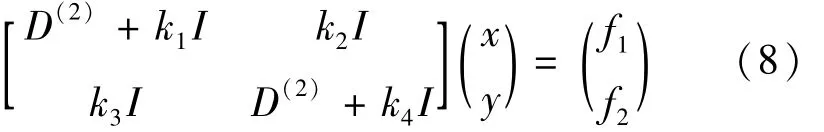
式中：D（2）为重心有理插值在时间节点 t1，t2，…，tn上的二阶微分矩阵；I为 n阶单位矩阵；k1、k2、k3、k4为常 数；x、y、f1、f2分 别 为 函 数 x（t）、y（t）、f1（t）、f2（t）在时间节点0＝t1，t2，…，tn＝T上函数值构成的列向量。

初始条件x（0）＝A、˙x（0）＝B、y（0）＝M，˙y（0）＝N，其中，A、B、M、N为常数，采用重心有理插值配点法将初始条件离散由式（9）表示为

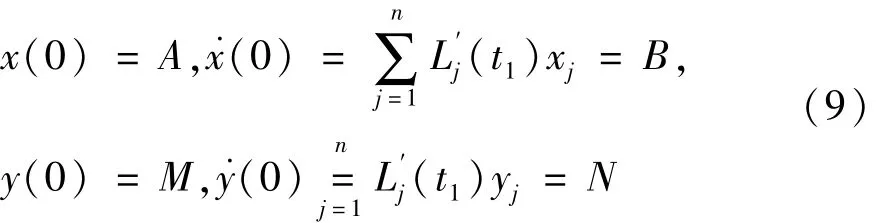
定义两个索引符号，其中 eni（i＝1，2，…，n）表示 n阶单位矩阵 I的第 i行向量；dni（i＝1，2，…，n）表示n阶微分矩阵D（n）第i行向量，初始条件可以写成矩阵的形式由式（10）表示为

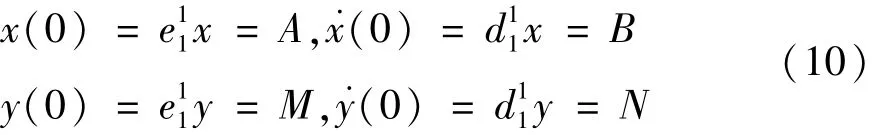
采用附加法施加初始条件式到式中，可求解代数方程式（11），得到线性振动控制方程数值解

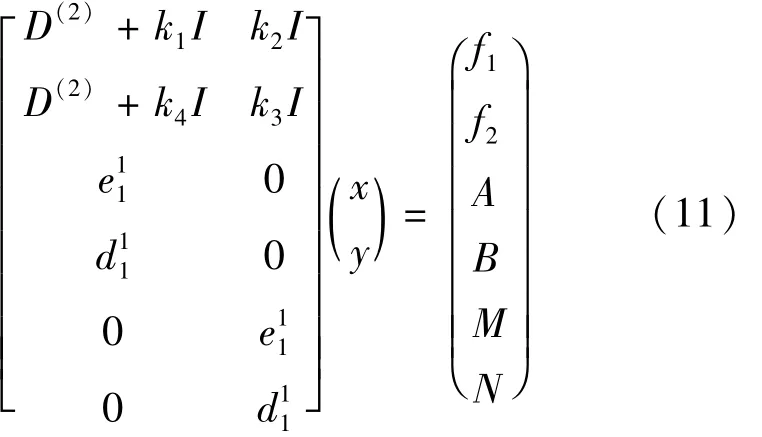
2 多自由度非线性系统的线性化迭代法

由于非线性公式千差万别，文章以具体的算例来说明多自由度非线性耦合系统的线性化迭代法的运用过程。采用控制方程在离散节点上的数值解同解析解差的最大值Ea‖uc－ue‖∞＝maxi｜uc－ue｜说明方法的计算精度，uc是数值解，ue是解析解。

算例1：如图1所示，k1为弹簧的刚度，k2为非线性弹簧的刚度，m为物体质量。该系统控制方程式（12）为［6］

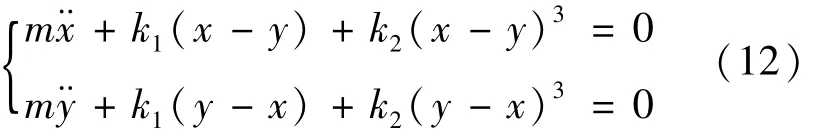
给定初始条件由式（13）表示为

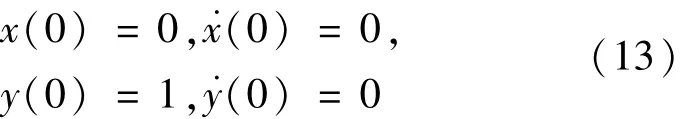
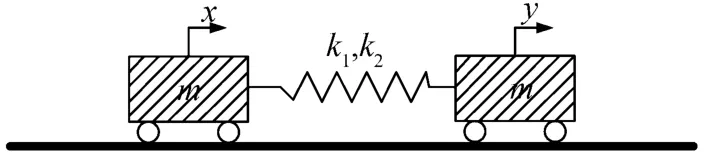
图1 由非线性弹簧连接的两个小车图

方程中含有立方非线性项，假定未知函数的一组初始解，，代入方程组中的非线性项，得到方程的线性化方程式（14）表示为

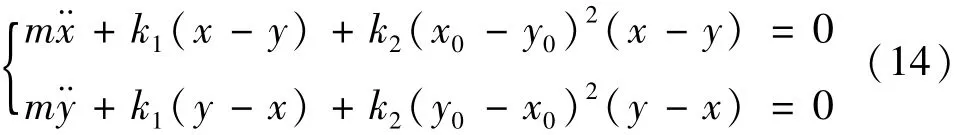
在给定的时间节点上 t＝［t1，t2，…，tn］T，采用重心有理插值配点法离散方程，可以得到方程的迭代式（15）为

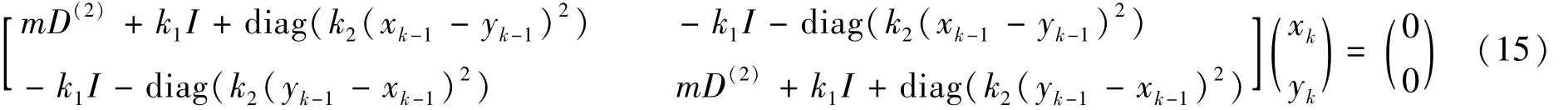
采用附加法施加初始条件式（13）到式（15），求解方程得到修正值xk，yk。给定控制精度ε，如果‖xk－xk－1‖∞＜ε且‖yk－yk－1‖∞＜ε，则xk和yk为非线性微分方程组的数值解，否则计算xk－1和yk－1直至数值解满足控制精度或达到设置的最大迭代次数为止。

3 数值算例

算例1的耦合系统参数为m＝1 kg，k1＝k2＝1 N／m，时间区域取［0，3］，时间节点t＝［t1，t2，…，tn］T分别采用等距节点和第二类Chebyshe点［18］。算例1解析解为［9］

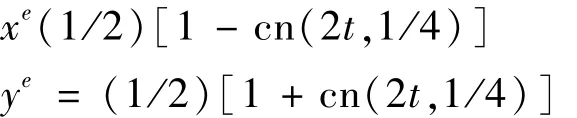
式中，cn为雅可比椭圆函数，60个节点重心有理插值迭代配点法计算解与解析解比较如图2所示。时间节点数量与数值解误差Ea＝maxi｜ue－ue｜和迭代次数的关系见表1。可以看出，采用较少数量节点，即可达到很高的计算精度。

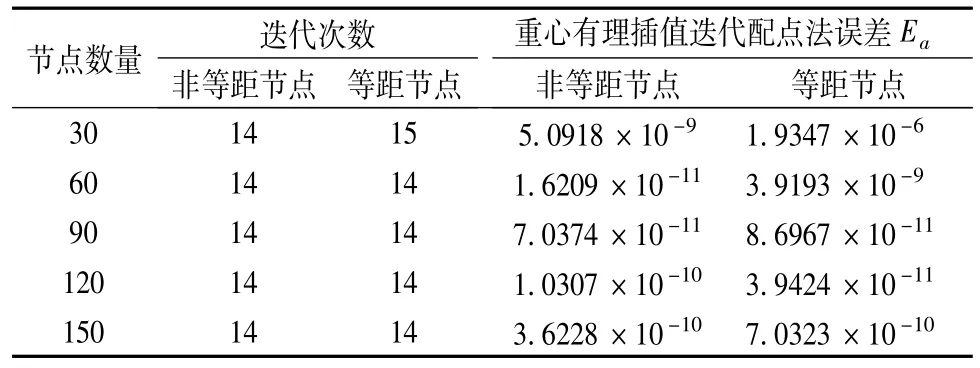
表1 算例1重心有理插值迭代配点法计算精度

算例2 如图3所示，k1为线性弹簧刚度，k2、k3为非线性弹簧刚度。该系统控制方程式（18）为［6］

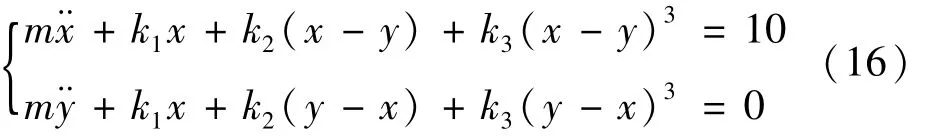
给定初始条件由式（19）表示为

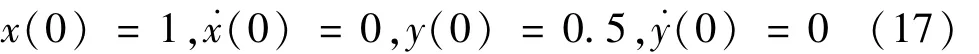
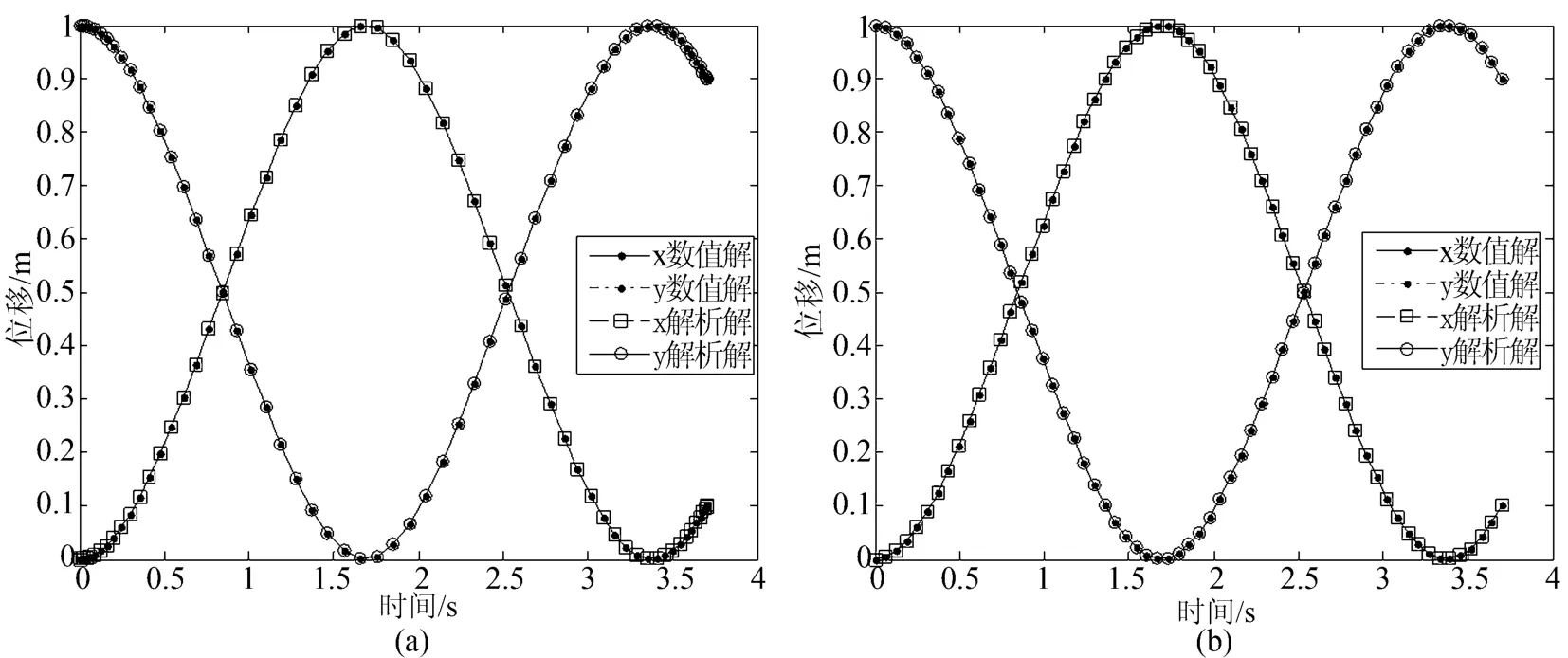
图2 算例1重心有理插值迭代配点法与解析解计算结果图

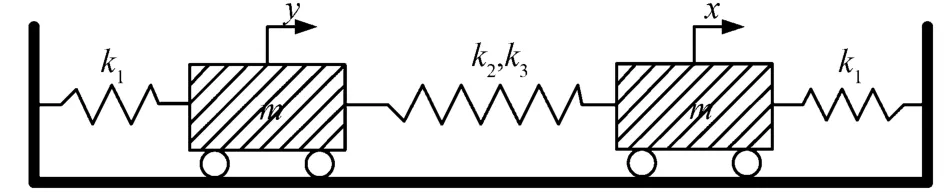
图3 双自由度耦合系统图

耦合系统参数为m＝1 kg，k1＝k2＝k3＝1 N／m，时间区域取［0，3］，时间节点 t＝［t1，t2，…，tn］T采用等距节点和第二类 Chebyshe点［18］。算例解析解为［8］

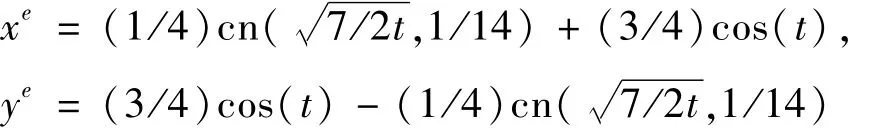
其中，时间节点数量与数值解误差 Ea＝maxi｜uc－ue｜和迭代次数的关系见表2。

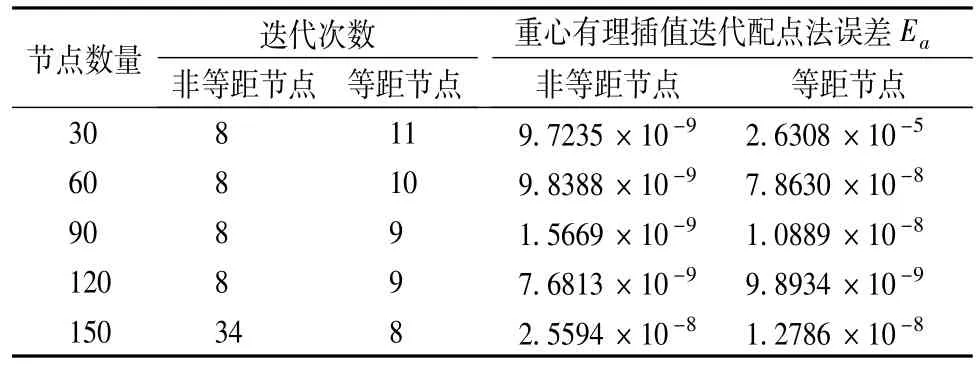
表2 算例2重心有理插值迭代配点法计算精度

4 结论

通过本研究可知：

（1）数值算例表明，重心有理插值迭代配点法求解多自由度系统非线性振动问题时具有非常高的计算精度，可快速得到时间节点处的高精度数值解。当处理大量节点尤其是等距节点时，有理插值仍能保持应有的计算稳定性。采用Lagrange多项式插值确定未知函数时，当节点数量很大时，计算矩阵接近奇异，因此，Lagrange多项式计算时不能采用数量较多的计算节点，限制了其计算精度的提高。

（2）在求解大跨度时间问题时，可以将求解区间分割为若干子区间，在每个子区间上采用重心有理迭代配点法计算，将前一区间末的函数值，作为下一区间计算的初始值，依次计算得到整个区间上节点的数值解。

［1］Moochhala Y.E.，Raynor S..Free vibration ofmulti-degree-offreedom nonlinear systems［J］.International Journal of Non-Linear Mechanics，1972，7（6）：651－661.

［2］Huang T.C..Harmonic oscillations of nonlinear two-degree-of-freedom systems［J］.Journal of Applied Mechanics，1995，22：107－110.

［3］Gilchrist A.O..The free oscillations of conservative quasilinear systemswith two-degrees-of-freedom［J］.International Journal of Mechanical Science，1961，3：286－311.

［4］Dimarogonas A.D，Haddad S..Vibration for Engineers［M］.New Jersey：Prentice-Hall，Englewood Cliffs，1992.

［5］Bayat M.，Shahidi M.，Barari A.，et al.The approximate analysis of nonlinear behavior of structure under harmonic loading［J］.International Journal of Physical Science，2010，5（7）：1074－1080.

［6］Bayat M.，Pakar I.，Shahidi M..Analysis of nonlinear vibration of coupled systems with cubic nonlinearity［J］.MECHANIKA，2011，17（6）：620－629.

［7］Ladygina Y.V.，Manevich A.I..Free oscillations of a nonlinear cubic system with two-degrees-of-freedom and close natural frequencies［J］.Journal of Applied Mathematics and Mechanics，1993，57：257－266.

［8］Cveticanin L..Vibrations of a coupled two-degree-of-freedom system［J］.Journal of Sound and Vibration，2001，247：279－292.

［9］Cveticanin L..Themotion of a two-mass system with non-linear connection［J］.Journal of Sound and Vibration，2002，252：361－369.

［10］Chen G..Applications of a generalized Galerkin'smethod to nonlinear oscillations of two-degree-of-freedom systems［J］.Journal of Sound and Vibration，1987，119：225－242.

［11］Jordan A.K..Modified Laplace Decomposition Method［J］.World Applied Sciences Journal，2012，18（11）：1481－1486.

［12］王兆清，唐炳涛，李树忱，等.求解间断边值问题的重心插值单元配点法［J］.山东建筑大学学报，2009，24（2）：115－118.

［13］Rashididinia J.，GhasemiM.，Jalilian R..A collocationmethod for the solution of nonlinear one-dimensional parabolic equations［J］.Mathematical Sciences，2010，4（1）：87－104.

［14］Yan J.P.，Guo B.Y..A collocation method for lnitial value problems of second-order ODEs by using laguerre functions［J］.Numer Math Theory Method Application，2011，4（2）：283－295.

［15］Geeta A.，Brajesh K.S..Numerical solution of Burgers'equation with modified cubic B-spline differential quadrature method［J］.Applied Mathematics and Computation，2013，224：166－177.

［16］段英峰，王兆清，林本芳.重心有理插值配点法分析矩形板自由振动［J］.山东建筑大学学报，2009，24（6）：434－437.

［17］Ordokhani Y..A collocation method for solving nonlinear differential equations via hybrid of rationalized haar functions［J］.Journal of Science，Tarbiat Moallem University，2007，7（3）：223－232.

［18］李树忱，王兆清.高精度无网格重心插值配点法—算法、程序及工程应用［M］.北京：科学出版社，2012.