自复位率对可控摇摆自复位钢框架抗震性能的影响

周星宇，李启才，纪瑞，韩平

（苏州科技学院土木工程学院，江苏苏州215011）

自复位率对可控摇摆自复位钢框架抗震性能的影响

周星宇，李启才，纪瑞，韩平

（苏州科技学院土木工程学院，江苏苏州215011）

耗能器和预拉力钢绞线的协同工作性能，是可控摇摆自复位结构的抗震设计主要考虑因素。通过理论分析该结构工作性能提出基于位移的性能化设计方法。在利用已有试验结果验证有限元方法的可行性后，采用OpenSees有限元软件对一个三层自复位结构进行了3组27个试件的时程分析，研究参数自复位率对结构抗震性能的影响。模拟分析结果表明：自复位率的增大能有效减小残余变形，但对峰值变形起放大作用，而这种放大作用与钢板耗能器的强度有关，因此需要将自复位率作为控制指标；将自复位率控制在0.625附近，能有效限制结构的震后残余位移，并使结构的层间侧移角峰值不致过大。

可控摇摆自复位钢框架；性能化设计；柱脚抬升；自复位率

作为满足结构性能化设计要求的一种新型结构[1]，可控摇摆自复位结构，通过放松柱脚节点，允许地震时自复位跨的一侧柱脚发生抬升，结合钢绞线提供的复位能力，从而使结构获得良好的抗震性能。可控摇摆自复位钢框架主要包含有三个部分：（1）钢框架，允许在地震荷载作用下柱脚发生抬升，但是限制水平方向变位；（2）垂直向钢绞线，主要提供侧向刚度和复位能力；（3）可更换的耗能元件，将地震能集中消耗在耗能元件上，减小梁柱等主要构件进入塑性的可能[2]。文中采用的是蝴蝶形钢板耗能器。

根据钢绞线和耗能器的摆放位置的组合，单跨可控摇摆结构共有如图1的四种类型，每种类型在抵抗倾覆荷载时都表现出不同的性能。对于预拉力钢绞线和耗能器都布置于跨中，见图1（a），当任何一侧柱脚抬起时，预拉力钢绞线和钢板耗能器都参与工作；而图1（b）是钢绞线布置于跨中，耗能器布置于两侧，在这种情况下，自复位跨一侧抬起时，只有一侧的耗能器发挥作用，而中间的钢绞线全部发挥作用，此时一侧的钢板耗能器在柱脚抬升比一样的情况下相比图1（a）变形更大，这对于充分发挥钢板耗能器的作用是有利的；图1（c）是钢绞线布置于两侧的情况，由于钢绞线布置于两侧，对一侧柱脚的力臂是图1（a）的两倍，因此在相同预拉力的情况下，结构在抬升后的后期刚度比图1（a）高，但是由于柱脚抬升相同高度时钢绞线变形相比放置于中间情况更大，且两侧的钢绞线不同时工作，分工明确；图1（d）图是钢绞线和钢板耗能器都布置于两侧的情形，柱脚抬升时，只有一侧钢绞线和耗能器参与工作且变形较大，两者都更容易进入塑性，设计时对钢绞线和钢板耗能器的强度极限都提出了更高的要求。

图1 单跨可控摇摆自复位结构

可控摇摆自复位结构的滞回曲线如图2（a）所示，结构力-变形图采用抗倾覆力矩和柱脚抬升率表示。其中抗倾覆力矩表示为

式中，MOT，R表示抗倾覆力矩；FPT表示钢绞线拉力；LPT表示钢绞线距离转动点的水平距离；Ffuse表示钢板耗能器提供的等效竖直力；Lfuse表示钢板耗能器至一侧转动点的水平距离；Gp表示自复位跨的结构自重；A表示自复位跨的跨长。

图2中各个点表示结构所处的不同工作状态，在侧向力较小时，可控摇摆自复位钢框架发生弹性变形，并主要依靠钢框架自身的弹性刚度抵抗倾覆力矩，柱脚不发生抬起；当倾覆力矩达到Mupi，钢框架的自身刚度已无法抵抗倾覆趋势时，一侧柱脚离开地面，此时，钢绞线开始伸长，钢板耗能器发生弹性变形；到达b点时，钢板耗能器发生屈服，结构耗能主要由钢板耗能器提供，此时的倾覆力矩为My，结构抗侧刚度转由钢绞线和钢板共同提供，由于钢板耗能器已经屈服，因此贡献的刚度仅为强化阶段对应刚度；到达c点后，即最大侧移角对应点后，结构卸载，整体向初始位置转动，钢绞线发挥复位效果，钢板耗能器也开始按照弹性路径卸载，此时结构的复位刚度与ab段的刚度相同；到达d点，钢板耗能器内力卸载到零，耗能钢板内力从此改为压力，此时钢板耗能器产生的反力开始抵抗结构的复位效果，当到达图中对应的e点时，钢板耗能器反向屈服；到达f点后，结构回复到初始位置[3]。

图2 结构滞回性能图

需要注意的是，重力在实际摇摆过程中对结构的抗倾覆起有利作用，Xiang MA[3]指出：在低层可控摇摆自复位钢框架结构（3～9层）中，重力作用提供的抗倾覆效果与钢绞线相比较不大，因此，对重力部分采取忽略不计的方法，这是保守的。

图2（b）、（c）表示在结构滞回过程中，钢绞线和钢板耗能器对应的工作状态以及对应重要关键节点所处状态，从图中可以看出预应力钢绞线在结构滞回过程中提供所需回复力，耗能器则承担了摇摆结构全部的耗能任务。因此，钢绞线回复力的大小决定了结构复位能力的强弱。

目前，受限于缺乏大量试验数据，自复位钢结构的合理化设计方法尚未系统提出。文献[4]针对摩擦型自复位支撑框架提出基于性能谱和底部剪力法的设计方法，与传统钢框架的设计方法不同的是，这种方法采用的是按照位移性能和延性指标两者结合的几何关系先设计阻尼器和预拉力构件，而后通过单自由度模型确定结构在设计地震作用下的强度和刚度，最后设计梁柱截面尺寸的思路。模拟结果表明：通过这种思路的设计，结构能够表现良好自复位性能。对于单跨可控摇摆自复位框架，文中参照其设计方法，结合本模型的性能特点，采用如下设计方法：

（1）根据设计性能目标确定与地震基底剪力和倾覆力矩有关的设计荷载；

（2）计算预拉力钢绞线和耗能器的强度分配；

（3）检查结构地震作用下的最大位移与性能谱法估算的进行对比，如果结果相差较大需要迭代设计；

（4）根据梁柱设计地震下内力设计梁柱尺寸。

由于耗能器和预应力钢绞线并不存在几何关系，两者的关系不能很快地确定，后面的模拟分析表明，这两者的性能对结构性能的影响并不是相互分离的。耗能器在结构正向加载时，参与分担了抗倾覆力矩，但当发生了塑性变形反向加载时，在自身弹性变形恢复后，耗能器实际上对钢绞线的回复功能起到抵抗作用，并抵消了一部分的抗倾覆力矩。抵消的抗倾覆力矩的大小取决于钢板耗能器的塑性刚度和强度。就单个构件而言，钢板耗能器强度过大过小，都会影响结构的复位效果和耗能能力；同样，钢绞线预拉力大小，会影响结构的复位效果和后期刚度；但是，两者对于结构抗震性能的影响不是独立的。根据这一特点，需要对钢绞线和耗能钢板的协同工作性能进行考虑。

为此，Eatherton[5]根据耗能器放置于柱间的双跨可控摇摆自复位钢框架，从倾覆力矩的角度提出了自复位率的概念，定义自复位率为钢绞线提供的复位力矩和耗能器提供的阻止复位力矩的比值，同时指出，将自复位率设置在0.33，最为经济合理，这样的设计不会使结构在循环荷载作用下留下过多的残余位移，保证结构的峰值侧移在限值以下。但是这一评价指标并不适用于耗能器放置于柱脚的单跨可控摇摆结构。对于在跨中设置耗能器和钢绞线的单跨可控摇摆自复位钢框架，Xiang.Ma[3]参照这个定义也提出了这个参数，但是和Eatherton不同的是，他定义自复位率为钢绞线预拉力和耗能器屈服荷载的比值，根据试验数据，考虑防止因钢绞线屈服造成的预应力损失和耗能器反向加载时的强化，仅仅从耗能器耗能最大考虑，粗略取为1.5，但是并没有对此做详细研究。事实上，将自复位率取为1.5对于设计耗能器放两边钢绞线放中间的情况是不合理的，结构会出现明显的残余变形。因此，文中从钢绞线和耗能器对抗倾覆力矩贡献程度的角度，定义自复位率通用公式如下

式中，FPT0表示钢绞线初始预拉力；其他参数同上。这种定义，物理意义明确，表示柱脚刚开始抬升时（同样忽略自重影响），钢绞线提供的抗倾覆力矩占总抗倾覆力矩的比例，方便设计时采用。下文将首先对有限元模拟方法进行试验验证，然后利用有限元分析得到自复位率的推荐取值。

1 有限元建模方法验证

采用有限元分析软件OpenSees研究自复位率对可控摇摆自复位结构抗震性能的影响。采用Ma.Xiang[3]在日本防灾科学研究所抗震工程研究中心进行的振动台实验所用的缩尺模型，试件平面图和模型简图如图3和图4所示，鉴于试验中，梁柱并未发生破坏，梁柱和支撑杆采用弹性梁柱单元模拟，钢绞线采用桁架单元，耗能器采用等效拉杆桁架单元，对试验中的A1J2和A1J5试件，进行了有限元时程分析验证，试验数据下载自美国Neeshub数据库。其中A1J2主要验证的是试件在50年超越概率为10%的地震响应，钢板耗能器采用的是Steel02材料，相对于steel01材料，这种材料能使曲线更加平滑，一定程度上更接近实际情况；而A1J5则是在50年超越概率为2%下结构响应，钢板耗能器采用了steel01材料。

图5和图6分别表示A1J5和A1J2的滞回曲线的对比结果（见表1），纵坐标表示钢绞线和钢板耗能器提供的倾覆力矩与屈服倾覆力矩比值。从图中可以看出，结构在罕遇地震下的滞回曲线展现出规则的旗帜形，结构复位性能良好，残余位移很小。A1J5的滞回曲线和试验曲线对比如图5所示，由于钢板耗能器采用了Steel01材料，这种材料的优点是本构简单，缺点是曲线较steel02材料光滑度低，因此曲线不圆滑，但是相关峰值以及曲线形状与试验曲线非常接近。试验2的滞回曲线和试验曲线对比如图6所示，不同的是钢板耗能器采用Steel02材料，地震动为46%的Kobe地震动，表示的是多遇地震工况，总体来说，模拟结果和试验结果吻合度较高，能捕捉到结构最大响应出现的时间和数值。验证结果表明设计方法基本正确，有限元方法可行。

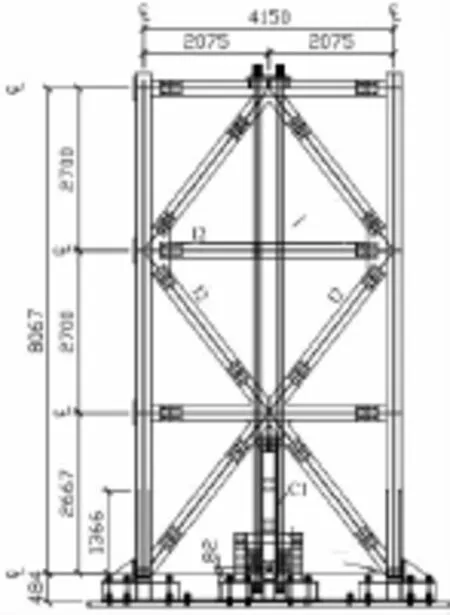
图3 试件简图

图4 模型简图

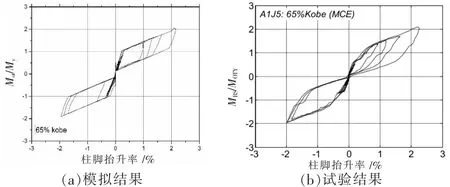
图5 A1J5试件滞回性能验证对比图

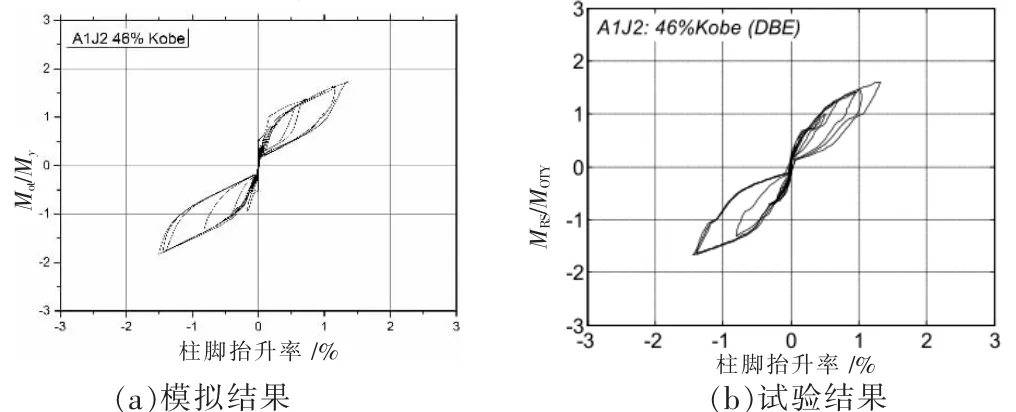
图6 A1J2试件滞回性能验证

表1 实验值与模拟值对比图

2 有限元模型分析

2.1 试件尺寸及模型参数的选取

参考抗震设计规范[6]设计模型的尺寸及设计参数。框架梁柱及支撑均采用了非线性梁柱单元，截面尺寸如表2所示。钢绞线同样采用桁架单元，采用两种本构组合的材料属性，材料参数参见表3，本构关系如图7。柱脚部位采用只压弹簧单元考虑水平向对柱脚限位和摇摆时的脱开现象。模型如图8所示，其中，框架跨度为6 m，每层层高4 m。

设置于柱脚的耗能器采用图9所示的蝴蝶形钢板，与前述方法一致，采用简化的桁架拉杆单元，布置于两侧柱脚，材料采用Steel02模拟，参数列于表4，等效耗能器拉杆强度计算公式采用文献[7]提出的公式。

式中，FfuseP为等效桁架单元屈服荷载；K为弹性模量，取2×105MPa；a，b为蝴蝶形连接的根部和中部宽度；t为钢板厚度；L为钢板长度；nL为蝴蝶形连接个数；σy为钢板耗能器屈服强度，取为235 MPa。

表2 梁柱及支撑截面尺寸mm

表3 预应力钢绞线参数

图7 钢绞线模型

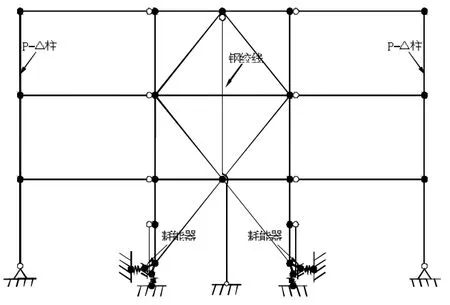
图8 模型平面图

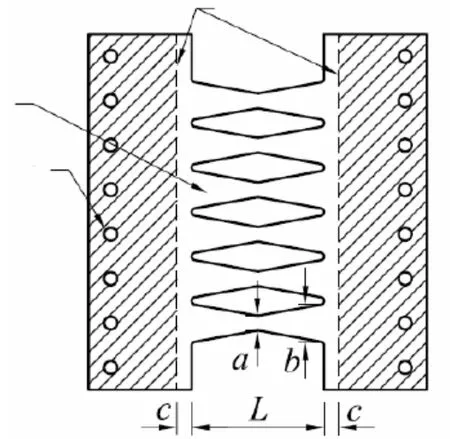
图9 蝴蝶形钢板耗能器简图

表4 钢板参数表

为了模拟重力的二阶效应，即周边结构的影响，在框架两侧增加P-Δ柱，参照FEMA355C[8]，将框架质量加载在P-Δ柱的节点上，并赋予柱较大的轴向刚度，较小的抗弯刚度，柱脚铰接，相关质量数值列于表5。

为验证设计模型的正确性，对所建模型进行了按照倒三角形分布加载的静力推覆分析，推覆曲线如图10所示。分析得到的柱脚初始抬升时的倾覆比为0.73，根据设计理论计算得初始柱脚抬升倾覆比0.727，模拟结果与理论计算结果一致。

根据我国抗震设计规范，结合文献[8]从美国太平洋地震中心选取了WHITTIER/ABUE250等6组天然地震波，并生成了2组人工波。由于篇幅限制，以具有代表性的WHITTIER/ABUE250为例，介绍模拟结果。首先对该地震波进行调幅，经调幅后的该地震波加速度时程曲线如图11所示。

表5 质量汇总表t

图10 静力推覆曲线

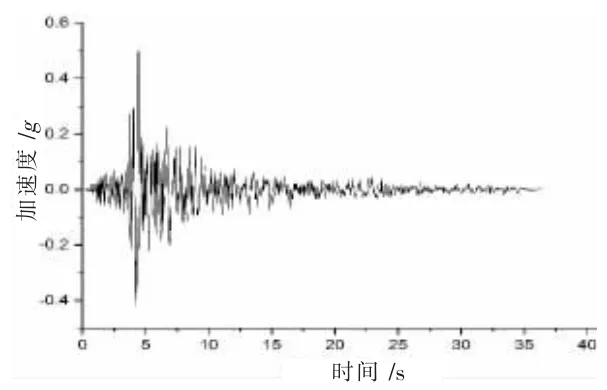
图11 地震动加速度反应谱

为了对比自复位率对结构复位耗能能力的影响，按照简化模型相应改变耗能器和钢绞线的面积，并保持预应力参数不变，对按自复位率和等效钢板耗能器的拉杆面积分类的27个试件进行了时程分析，具体参数如表6所示。

表6 钢绞线面积表mm2

2.2 结果分析

由于试件较多，取等效耗能期拉杆面积为3 000 mm2的一组试件为例，根据自复位率变化钢绞线面积，并保持预应力不变，得到的滞回曲线如图12所示，可以看出，随着自复位率的提高，曲线的最大柱脚抬升比先增大后略有减小，但同时，残余变形减小，当自复位率很小时，结构的滞回响应接近普通弹塑性钢框架的滞回反应，随着自复位率的增大，捏缩现象变得明显，曲线形状变为旗帜形，自复位结构特征变得更加明显。

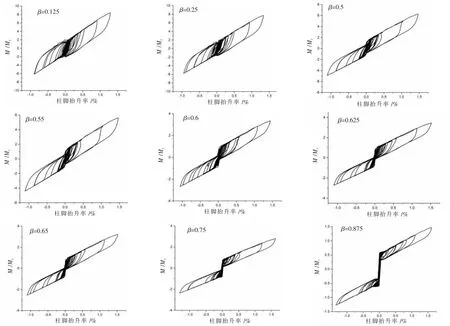
图12 滞回曲线

为了具体研究不同自复位率对结构的复位性能、最大响应和耗能性能的影响，将结构地震中的残余变形、最大响应、耗能能量大小与β的关系图分别列于图13～15，图中实线、点线、点划线分别表示等效耗能器的拉杆的面积（mm2）。

图13 残余变形变化表

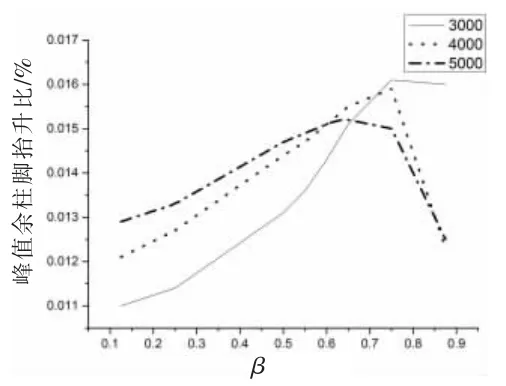
图14 最大柱脚抬升比变化表

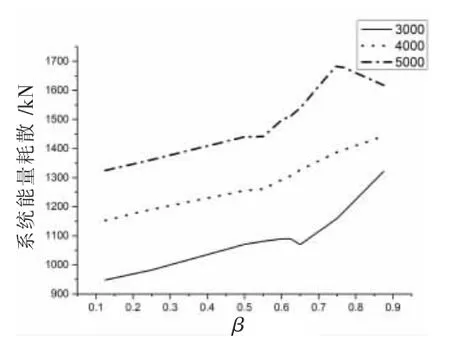
图15 耗能情况表

从图13～14可见，随着β值的增大，柱脚抬升比峰值经历了由小到大再变小、残余变形从大变小的过程，而地震中结构耗能呈先放大、而后略有减小趋势。脚抬升比峰值经历了由小到大再变小，峰值变形从小变大再变小，经过简单计算，在整个时程分析进程中，柱中峰值应力为107 MPa，小于屈服应力345 MPa，因此，柱没有进入塑性。可见，自复位率的增大对地震过程中结构的最大位移有不利影响，并不是因为过大的预拉力使得框架部分位置出现了塑性所致，有学者[11]指出，峰值变形随着自复位率增大，可能是因为蝴蝶形钢板在滞回过程中在面外发生了扭转屈曲，使结构抗倾覆刚度急剧下降，从而峰值变形发生了增大，而后期由于钢绞线预拉力的继续增大完全补偿了由于钢板耗能器的面外屈曲造成的影响，因此，峰值变形略有下降。自复位率从0.125变化到0.75，峰值变形增大了45.5%，因此设计时，过大的变形，对地震过程中缓解人员恐惧心理和正常有序疏散的影响是需要考虑的，如果简单从减小残余变形考虑盲目增大预拉力，是不理想的，也是不经济的。耗能能力由小变大再略有减小，这是因为随着预拉力的增大，虽然曲线出现了捏缩，但是曲线峰值变形的增大超过了捏缩幅度，这样的结果使得滞回环面积（耗能）增大，而随着预拉力继续增大，曲线捏缩使滞回曲线面积减小的幅度超过了峰值变形使滞回环面积增加的幅度，因此耗能会略有下降。从曲线中还可以看出，结构能否发挥自复位结构性能优势，不仅取决于钢绞线，还取决于钢板耗能器的强度和刚度，两者存在着紧密的协同工作关系。研究自复位率β的合理取值，对于可控摇摆自复位钢框架性能化抗震设计，是有必要的。

从图13～15可以看出，变化钢板耗能器的强度和刚度，对于结构残余变形的影响较小；对于结构峰值变形，在自复位率较小时，钢板耗能器的影响较大，而随着自复位率的增大，影响减小；对于结构耗能能力的影响，钢板耗能器的影响较大，这也和前人的结论一致[5]。

还可以看出，β值对于结构残余变形的影响在0～0.7区间最为明显，大约β值等于0.625时，结构的残余变形降低到了0.2%以下，而峰值变形并没有增加过大，耗能能力较好，此时，增大自复位率，虽然能够减小残余变形，但是结构峰值变形会相应变大，耗能能力的提升有限，同时框架结构自身进入塑性的可能性会增大，设计施工考虑避免梁柱等主要构件破坏而增加的成本相应提高，这将提高整体结构的造价。因此，从经济和安全角度，盲目增大自复位率是不合理的。因此，建议将自复位率β取为0.625附近较为合理。

3 结语

（1）得到单跨可控摇摆自复位框架的设计方法，证实提出的自复位率的概念的必要性；

（2）提高自复位率能够有效减小结构震后残余变形，但是对结构的峰值变形可能有不利影响；

（3）可控摇摆自复位钢框架中，钢绞线和耗能器的协同工作性能对结构的复位性能和耗能能力有重要影响，采用自复位率作为评价和设计可控摇摆自复位结构的重要指标是合适的；

（4）综合考虑结构耗能、峰值变形、残余变形限值，针对本文所研究的耗能器布置于柱间的这类结构，将自复位率取为0.625时能够保证所研究的大部分试件在罕遇地震作用下残余变形满足要求，并使峰值变形不致过大，同时保证结构的耗能能力。

当然研究仍然存在很多不足之处，仅从整体上对自复位率的影响做了简要分析，对耗能器做了很大的简化，对于耗能器面外屈曲等局部性能变化问题考虑较少，需要后续研究提出更精确的公式以使模拟结果更接近实际。

参考文献：

[1]周颖，吕西林.摇摆结构及自复位结构研究综述[J].建筑结构学报，2011，32（9）：1-10.

[2]Eatherton M R,Ma X,Krawinkler H,et al.Design concepts for controlled rocking of self-centering steel-braced frames[J].Journal of Structural Engineering,2014,140（11）：1-10.

[3]Ma X.Seismic Design and Behavior of Self-Centering Braced Frame with Controlled Rocking and Energy-Dissipating Fuses[M].Stanford University,USA,2010.

[4]Zhu S,Zhang Y.Performance based seismic design of steel braced frame system with self-centering friction damping brace[C]//Proceedings of the 18th analysis and computation specialty conference,2008.

[5]Eatherton M R,Hajjar J F.Residual drifts of self-centering systems including effects of ambient building resistance[J].Earthquake Spectra,2011, 27（3）：719-744.

[6]中国建筑科学研究院.GB 50011-2010建筑抗震设计规范[S].北京:中国建筑工业出版社，2010.

[7]Deierlein G G,Ma X,Eatherton M,et al.Collaborative research on development of innovative steel braced frame systems with controlled rocking and replaceable fuses[C]//Proc.6th International Conference on Urban Earthquake Engineering,Tokyo,2009:413-416.

[8]SAC Joint Venture.FEMA-335C,State of the art report on systems performance of steel moment frames subject to earthquake ground shaking[M]. USA,2000.

[9]杨溥,赖明.结构时程分析法输入地震波的选择控制指标[J].土木工程学报,2000,33（6）：33-37.

[10]Eatherton M,Hajjar J,Ma X,et al.Seismic design and behavior of steel frames with controlled rocking-Part I:concepts and quasi-static subassembly testing[C]//Proc.,ASCE/SEI Structures Congress 2010,2010.

[11]Hall K S,Eatherton M R,Hajjar J F.Nonlinear behavior of controlled rocking steel-framed building systems with replaceable energy dissipating fuses[R].Newmark Structural Engineering Laboratory.University of Illinois at Urbana-Champaign,USA,2010.

The influence of self-centering ratio on seismic performance of controlled-rocking steel frames

ZHOU Xingyu,LI Qicai,JI Rui，HAN Ping
（School of Civil Engineering,SUST,Suzhou 215011,China）

s：Coordination of the energy consumer and pre-tensioning stranded fuse plays an important role in the seismic design of the controlled-rocking self-centering steel frame.Based on the theoretical analysis of the seismic performance of the structure,a displacement-based design is introduced.The open-source software OpenSees is used to conduct the nonlinear time-history analysis of 27 specimens of 3 groups in a 3-layer selfcentering structure after the validation of the result of the experiment,which is used to study the impact of the parameter self-centering ratio on the seismic performance.The results indicate that the increase in the self-centering ratio can significantly reduce the residual uplift ratio,but has an amplification effect on the peak displacement under the designed earthquake.The amplification has some relation to the rigidity of the energy consumer, so the self-centering ratio should be taken as a control index.What's more,the control of the self-centering ratio around 0.625 will effectively limit the residual deformation below the limit value from the standard after the earthquake,and ensure that the peak value of uplift ratio is not too large.

self-centering steel frame with controlled rocking;uplift ratio of the column base;self-centering ratios

TU391

A

1672-0679（2015）04-0030-07

（责任编辑：秦中悦）

2015－04-10

国家自然科学基金项目（51378326）；江苏省结构工程重点实验室开放课题（ZD1204）

周星宇（1987-），男，江苏南通人，硕士研究生。

李启才（1969-），男，河南灵宝人，博士，副教授，从事钢结构新型体系和抗震设计，E-mail：ustsgjg@163.com。