近场地震下人字形中心支撑钢框架基于能量的性态设计方法

宋彬，顾强

（苏州科技学院土木工程学院，江苏苏州215011）

近场地震下人字形中心支撑钢框架基于能量的性态设计方法

宋彬，顾强

（苏州科技学院土木工程学院，江苏苏州215011）

在基于能量的性态设计中，不能以结构的累积滞回能作为设计依据，应该以引起结构瞬间破坏的那部分有效能量作为设计依据。介绍了近场地震的特征及最大有效滞回耗能（MECE）谱的概念，提出了近场地震下人字形中心支撑钢框架基于MECE谱的性态设计方法；设计了一个人字形中心支撑钢框架；采用Pushover和时程分析方法评估了该结构的地震反应及能量分布，并证明了设计方法的可信性。

近场地震；中心支撑钢框架；性态设计方法；最大有效滞回耗能；时程分析

基于能量设计方法的核心是地震输入给结构的总能量必须与结构存储、转换和耗散的能量相平衡[1]。Bertero和Uang[2]提出了两种计算地震动输入能量的方法，一种是根据绝对运动来计算地震的输入能，另一种则根据相对运动来计算输入能。两种计算方法的动力平衡方程形式相同，但动能和输入能的定义不同。Bruneau[3]的研究表明根据相对运动来计算输入能更为合理。

近场地面运动的两个重要特征是强速度脉冲和永久性地面位移[4]。地震波的单个强速度脉冲或系列长周期的高振幅速度脉冲导致在很短时间内对结构输入了较大的能量，使结构瞬时达到最大响应，产生严重破坏。为了寻求近场地震下更为合理的滞回能设计依据，文中参考文献[5]选用总滞回耗能的部分能量，即单自由度体系达到目标延性时第一象限或第三象限中骨架曲线所包络的单向推覆能量作为滞回能设计依据，文献[5]称为最大有效滞回耗能（MECE），见图1中阴影面积OABCO。图1中，ut为体系的目标延性，uy为体系的屈服位移、Vy为体系的屈服剪力，k为体系的刚度，p为体系的后期刚度系数。

图1 最大有效滞回耗能

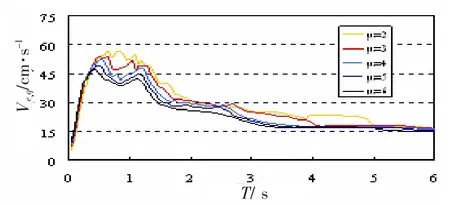
图2 最大有效滞回耗能等效速度谱（罕遇地震水准）

图2为文献[5]提出的罕遇地震水准下后期刚度p=0.05、阻尼比ζ=0.05、目标延性比μ=2、3、4、5、6时的最大有效滞回耗能的等效速度Veq谱。Veq与MECE的关系见公式（1），m为系统质量。

1 人字形中心支撑钢框架性态设计基本步骤

近断层地震下人字形中心支撑钢框架基于MECE的设计采用如下假定：

（1）带支撑榀框架承担全部地震水平力，其余框架只承担竖向荷载。

（2）罕遇地震下带支撑榀框架的破坏模式为支撑屈服或屈曲，钢梁两端、底层框架柱根部形成塑性铰，如图3所示。

步骤1：结构截面初选及自振周期计算。根据设计资料与相关规范，只考虑竖向荷载组合，用PKPM初步选择截面。用Sap2000软件对结构进行模态分析得到周期和振型。

步骤2：确定结构的屈服位移及整体位移目标延性系数。受拉支撑屈服时受压支撑已经屈曲，故计算楼层屈服位移以受拉支撑屈服为依据。基于图4小变形分析可推导出中心支撑结构的楼层屈服位移。

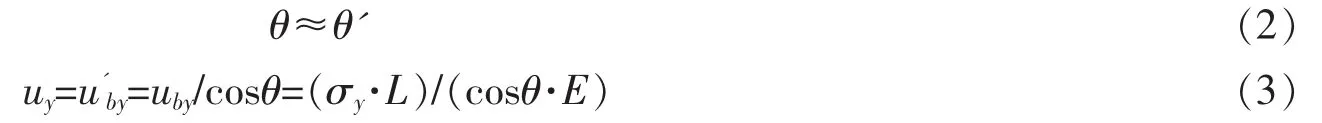
式中，L为拉杆的长度，θ为支撑杆与水平线夹角，uy为楼层的屈服位移，E为材料的弹性模量，其他参数如计算简图标注所示。

参考杨俊芬[6]对人字形中心支撑钢框架的整体延性分析结果，人字形中心支撑钢框架结构的整体位移延性系数取μt=3.0。

步骤3：计算最大有效滞回能需求。根据步骤1得到的结构各阶自振周期、步骤2得到的结构整体延性系数，直接从最大有效滞回耗能等效速度谱（见图2）查出对应前n阶的等效速度，即Vh,1、Vh,2……Vh,n计算出对应各阶振型的等效单自由度（ESDOF）体系的滞回能需求。参考文献[7]，采用公式（4）～（8）计算弹塑性多自由度结构最大有效滞回耗能需求。

式中，Eh（MDOF）为多自由度结构的最大有效滞回能需求，Eh（ESDOF），j为对应结构第j振型的等效单自由度体系最大有效滞回能需求，Vh,j为第j周期所对应的等效速度，Γj为第j振型的参与系数，M为多自由度体系的质量矩阵，M*j为第j振型等效单自由度体系的广义质量，mi为第i楼层的质量，φij为第j振型在第i楼层的振幅，Xmass，j为第j振型的振型质量参与系数，N为结构的振型数，n为结构的层数。为了能够获得合理的总有效滞回耗能，应该保证振型质量参与系数之和大于90%，在一般情况下，取结构的前三阶振型就可满足要求。

步骤4：侧向力分布模式的确定。采用文献[8]基于偏心支撑钢框架非线性时程分析得到的剪力分布系数βi作为人字形中心支撑钢框架弹塑性状态下侧向力分布模式，如公式（9）～（11）所示。

式中，n为结构总层数；βi为第i层的剪力分布系数；Vi、Vn分别为第i层和顶层（第n层）的楼层剪力；Wi、Wj分别为第i和第j层的重量；hi、hj分别为第i层、第j层距地面的高度；Wn为结构顶层的重量；hn为楼顶距地面的高度；T为结构的基本周期；Fi、Fn分别为作用在第i层和顶层n的侧向力；V为设计基底剪力。

步骤5：计算设计基底剪力。根据结构单向达到最大侧移时的滞回耗能与近场地震作用的最大有效滞回能需求相等的原则建立能量平衡关系。结构单向达到最大侧移时的滞回耗能由支撑、梁端及柱底三部分构成。平衡关系如公式（12）所示。

令各层支撑分担的层剪力分布也符合式（9）～（11），根据中心支撑杆件的滞回耗能的计算方法代入式（12）可以得到式（13）。将剪力分布系数式（14）和式（15）代入式（13）中可得出中心支撑钢框架的支撑所分担的底部设计剪力，见式（16）。

式中,ΔEh，b为钢梁塑性铰的最大有效滞回耗能；ΔEh，c为钢柱根部塑性铰的最大有效滞回耗能；ηd为中心支撑杆滞回环捏缩系数；Vd，i为第i层一对支撑杆的抗剪承载力；uy，i为第i楼层屈服位移；pd，i为第i层中心支撑杆的后期刚度系数；μt，i为第i层的目标延性；θp,i为第i层中心支撑框架结构的层间塑性转角；θr,i为罕遇地震下中心支撑框架结构第i层的层间侧移角；θy,i为第i层中心支撑框架的层间屈服侧移角。hs，i为第i层的层高，其他参数同前。

由公式（9）～（11）可计算出第i层支撑分担的层剪力

步骤6：构件设计方法。支撑杆设计，第i层支撑的抗剪承载力需满足

其中，VCBF，i为第i层支撑的抗剪承载力，Vd，i为基于有效滞回能计算所得第i层支撑的强度需求，Nb，i为受压杆屈曲后的承载力,Ny，i为受拉杆屈服后的承载力,θi为第i层支撑与水平线的夹角。钢支撑截面应该满足式（19）的要求。同时需要满足文献[9]的长细比、板件宽厚比要求。

支撑跨梁设计。文献[9]规定人字形支撑的横梁在支撑连接处应保持连续，应承受支撑斜杆传来的内力，并宜计入受压支撑屈曲后产生的不平衡力。为了能够得到钢梁的最大弯矩，考虑到梁端部已形成塑性铰，可将支撑跨梁视为简支梁验算跨中弯曲强度，结构的屈服机理和横梁的计算简图如图5所示。

钢柱设计。钢梁两端及支撑因地震作用而形成塑性铰后，钢柱承担了结构大部分的倾覆力矩及竖向荷载，使左右两侧钢柱分别受到拉力和压力作用[10]。为了保证结构在受到地震作用时，不会因为钢柱失稳而产生破坏，可根据钢柱的受力对其进行强度和平面内、外稳定验算。

图3 人字形中心支撑钢框架罕遇地震下的塑性机构

图4 楼层屈服位移计算简图

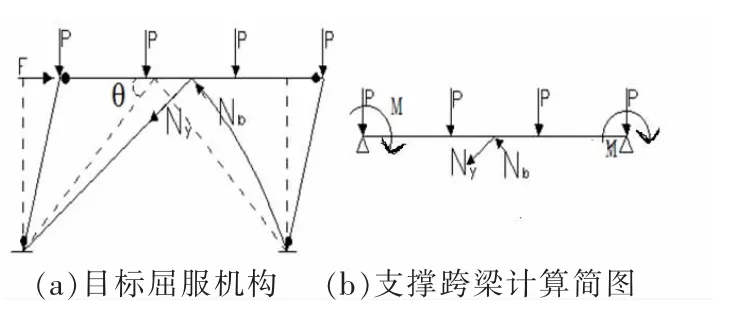
图5 支撑跨梁受弯计算简图

2 结构设计实例

10层中心支撑钢框架结构，设防烈度8度（0.3g），Ⅱ类场地，地震分组为第一组。层高3.3 m，次梁间距2.6 m，Q345钢材。每个方向各布置2榀带支撑框架。楼面恒荷载和活荷载分别为4.5和2.0 kN/m2，屋面恒荷载和活荷载分别5.0和2.0 kN/m2，雪荷载为0.5 kN/m2。外围护玻璃幕墙荷载标准值为1.5 kN/m2，梁、柱及支撑自重1.1 kN/m。女儿墙高1.1 m，厚度0.24 m，荷载标准值19 kN/m3。结构平面布置见图6，剖面见图7。

图6 结构平面布置

图7 2-2轴线剖面

利用sap2000软件对初选截面进行模态分析，得到结构的振型、周期。结构前3阶的自振周期分别为T1= 1.192 s、T2=0.399 s、T3=0.233 s。根据MECE谱（见图2）可得到前3阶的等效速度分别为VMECE,1=48.8 cm/s、VMECE,2=49.7 cm/s、VMECE,3=35.9 cm/s，见图8。由上节所述设计方法计算出各层支撑分担的剪力，见表1。对各构件进行设计最终确定的构件截面如表2所示。

表1 10层结构各层支撑分担剪力

表2 梁、柱、支撑截面

3 算例结构分析

为了证明方法设计的人字形中心支撑钢框架结构的可靠性，采用Pushover和弹塑性时程分析法对其进行了评估。Pushover分析采用sap2000软件，弹塑性时程分析采用ABAQUS软件。

3.1 Pushover分析

进行pushover时根据文献[11]的建议对梁端、支撑及柱端的塑性铰进行修改。Pushover推覆采用公式（9）～（11）的侧向力分布模式。图9为结构最大层间侧移角达到0.02时的屈服模式。

由图9可以看出当结构的最大层间侧移角到达0.02时，结构的大部分支撑、楼层梁两端以及柱底出现了塑性铰。屈服模式与设计假定基本一致，说明假设的结构屈服模式合理。

3.2 弹塑性时程分析

时程分析选波原则如下：

（1）地震震级6.5级；

图8 前3阶周期的等效速度

图9 pushover结果

（2）地震波的卓越周期接近场地的特征周期[12]；

（3）为使所选地震波有明显的速度脉冲[13]，PGV/PGA>0.2；

（4）将所选地震波峰值加速度调到小震，对结构进行弹性时程分析得到结构底部剪力，对每条时程曲线计算所得结构底部剪力不应小于振型分解反应谱法计算结果的65%，多条时程曲线计算所得结构底部剪力不应小于振型分解反应谱法计算结果的80%。

根据以上条件终选的10条地震波见表3。

表3 结构所选地震波

根据连尉安[14]的支撑滞回性能有限元模拟结果以及杭晓晨[15]等的振动台实验的有限元模拟分析，进行ABAQUS建模时，支撑及梁柱均采用B32梁单元。

ABAQUS可以输出结构的滞回耗能和位移时程。得到结构最大有效滞回耗能的计算方法是：通过顶点位移时程找出结构产生最大顶点位移的时刻和产生最大位移前位移为零的时刻，记为t1和t2；在能量时程上找出相对应的时间点，最大有效滞回耗能就等于总滞回耗能在t1和t2时刻间的差值。图10为算例结构在P1182（510 gal）地震波作用下的顶点位移时程曲线，从图中可以确定位移最大点所对应的时刻t1及产生此最大位移前位移为零的最近时刻t2；在能量时程（见图11）上找出对应的t1和t2，图11所示的能量差即为最大有效滞回耗能。

图12和13为算例结构在多遇和罕遇地震作用下的层间位移角包络图。可见算例结构在多遇和罕遇地震下除个别地震波外，层间位移角基本都没有超过规范的限值。结构层间位移角包络值从底层向上开始变大，在中上部楼层达到最大值，然后又随高度的增加而变小。总的来说，结构的层间位移角包络值从上到下变化比较均匀，虽然中下部楼层位移角偏大，但不存在突变，说明所设计的结构不存在明显的薄弱层，设计方法合理。图14为罕遇地震下结构的最大有效滞回耗能层间分布图。可以看出近场地震作用下人字形中心支撑钢框架的最大有效滞回耗能主要分布在结构高度中部和底部。产生这种现象的原因可能是地震波速度脉冲的周期与结构第一振型周期比较接近而产生了共振，此时结构高层部分的耗能比较小。结构的有效滞回耗能在楼层的分布变化是比较均匀的，未出现很大的突变，说明结构中不存在明显的薄弱层，再次证明了文中设计方法的合理性。

图10 时间点确定

图11 能量差

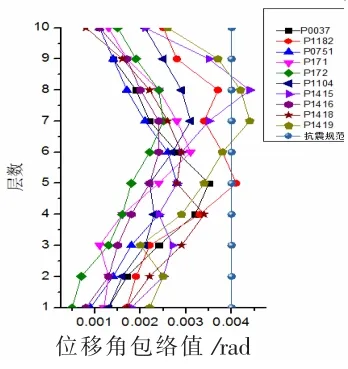
图12 多遇地震位移角

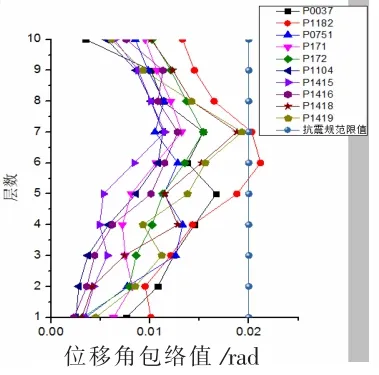
图13 罕遇地震位移角

图14 层滞回耗能

4 结语

（1）利用最大有效滞回耗能谱能够准确计算结构在近场地震下由速度脉冲而产生的最大有效滞回耗能，概念清晰，计算方便。（2）基于能量的性态设计方法相对于传统基于强度的弹性设计方法能更好地反映结构在非弹性阶段的性能，保证结构在弹塑性阶段出现理想的延性屈服模式，控制构件塑性发展与破坏程度。（3）文中方法设计的结构层间侧移与层间滞回耗能分布都比较平均，没有出现明显的薄弱层，表明结构整体协同工作，各层构件都得到了较充分的利用。（4）在基于最大有效滞回耗能设计人字形中心支撑钢框架时，应该注意结构的能量需求和耗能能力的不同概念。（5）在进行构件能力设计时，要区分不同构件的受力特征。

[1]Housner G W.Limit design of structure to resist earthquake[C]//Preceding of First World Conference on Earthquake Engineering.Earthquake Engineering Research Institute,Berkeley,USA,1936:1-11.

[2]Uang C M,Bertero V V.Use of Energy as a Design Criterion in Earthquake-Resistant Design[R].Earthquake Engineering Research Center,University of California,Berkeley,California,USA,1988.

[3]Bruneau M,Wang N.Some Aspects of Energy Methods for the Inelastic Seismic Response of Ductile SDOF Structures[J].Engineering Structures, 1996,18（1）：1-12.

[4]李明，谢礼立，杨永强，等.基于反应谱的近断层地震动潜在破坏作用分析[J].西南交大学报，2010，45（3）：331-335.

[5]孙国华，顾强，何若全，等.近断层地震作用下钢板剪力墙结构基于MECE谱的性态设计方法[J].建筑结构学报，2012，33（5）：105-117.

[6]杨俊芬.中心支撑钢框架的结构影响系数和位移放大系数研究[D].西安：西安建筑科技大学，2009.

[7]孙国华，顾强，何若全，等.基于滞回耗能谱的钢板剪力墙结构性态设计方法[J].建筑结构学报，2011，32（11）：126-133.

[8]Shih-Ho Chao.Performance-based seismic design of EBF using target drift and yield mechanism as performance criteria[R].University of Michigan College of Engineering,Michigan,USA,2005.

[9]中国建筑科学研究院.GB 50011-2010.建筑抗震设计规范[S].北京:中国建筑工业出版社，2010.

[10]李玉荣，蔡康峰，唐月.中心支撑-框架钢结构设计与研究[J].工业建筑，2010，40（6）：116-130.

[11]沙广璟，何若全．SAP2000在静力弹塑性分析时时程塑性铰的修改[J]．苏州科技学院学报：工程技术版，2007，20（3）：1-4.

[12]李慧.中，美，欧，日建筑抗震规范地震作用对比研究[D].哈尔滨：哈尔滨工业大学,2011.

[13]韦韬，赵凤新，张郁山.近断层脉冲速度脉冲的地震动特性研究[J].地震学报，2006，28（6）：629-637.

[14]连尉安.焊接工字形钢支撑低周疲劳性能及其应用研究[D].哈尔滨：哈尔滨建筑大学，2006.

[15]航晓晨.人字形中心支撑钢框架滞回能需求层间分布规律[D].苏州：苏州科技学院，2013.

Energy-based seismic design of Chevron concentrically braced steel frames under the near-field earthquake

SONG Bin,GU Qiang
（School of Civil Engineering,SUST,Suzhou 215011,China）

In the energy-based seismic design,the efficient energy which causes the instant failure of structures should be picked up as a basis of the design instead of the total hysteretic energy of the structure.This paper introduces the features of the near-field earthquake and the concept of MECE,provides the design for a Chevron concentrically braced steel frame in accordance with the MECE spectrum,and designs a Chevron concentrically braced steel frame.In order to evaluate the rationality of the design,this paper uses Pushover and the time history analysis to calculate the reaction and energy distribution of the example.

near-field earthquake;concentrically braced steel frame;Performance based on seismic design;the MECE spectrum;time history analysis

TU391

A

1672-0679（2015）04-0024-06

（责任编辑：秦中悦）

2015－04-28

国家自然科学基金项目（51278320）

宋彬（1989-），男，江苏苏州人，硕士研究生。